3.7.1. Общие сведения.
Качество работы любой системы управления в конечном счете определяется величиной ошибки, равной разности между требуемым и действительным значениями управляемой величины:
 .
.
Знание мгновенного значения ошибки в течение всего времени работы управляемого объекта позволяет наиболее полно судить о свойствах системы управления. Однако в действительности вследствие случайности задающего и возмущающего воздействий такой подход не может быть реализован. Поэтому приходится оценивать качество системы по некоторым ее свойствам, проявляющимся при различных типовых воздействиях. Для определения качественных показателей системы в этом случае используются так называемые критерии качества.
В настоящее время разработано большое число различных критериев качества. Все их можно разбить на четыре группы.
К первой группе относятся критерии, в той или иной степени использующие для оценки качества величину ошибки в различных типовых режимах. Эту группу назовем критериями точности систем управления.
Ко второй группе относятся критерии, определяющие величину запаса устойчивости, т. е. критерии, устанавливающие, насколько далеко от границы устойчивости находится система.
Почти всегда опасной для системы является колебательная граница устойчивости. Это определяется тем, что стремление повысить коэффициент передачи разомкнутой системы, как правило, приводит к приближению замкнутой системы именно к колебательной границе устойчивости и затем — к возникновению незатухающих колебаний.
Третья группа критериев качества определяет так называемое быстродействие систем управления. Под быстродействием понимается быстрота реагирования системы на появление задающих и возмущающих воздействий. Наиболее просто быстродействие может оцениваться по времени затухания переходного процесса системы.
К четвертой группе критериев качества относятся комплексные критерии, дающие оценку некоторых обобщенных свойств, которые могут учитывать точность, запас устойчивости и быстродействие. Обычно это делается при помощи рассмотрения некоторых интегральных свойств кривой переходного процесса.
При рассмотрении понятий запаса устойчивости и быстродействия можно исходить из двух существующих в настоящее время точек зрения.
Во-первых, можно основываться на характере протекания процессов во времени и использовать для формирования критериев качества переходную или весовую функцию, расположение полюсов и нулей передаточной функции замкнутой системы и т. п.
Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившемся режиме при действии на входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика и др.
Оба эти подхода имеют в настоящее время большое распространение и используются параллельно. И тот и другой подход требует изучения условий эксплуатации уже построенных систем автоматического управления, так как только на основании такого изучения можно правильно сформулировать количественные оценки, которые могут быть использованы в практике проектирования и расчета новых систем.
Показатели качества переходных процессов.
Ошибка регулирования
Для оценки точности используется ошибка регулирования
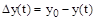 ,
,
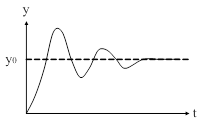
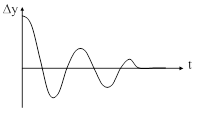
которая с течением времени стремится к некоторому постоянному значению (рис. 75), называемому статической ошибкой:
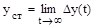 .
.
Таким образом, статическая ошибка равна разности между установившимся значением регулируемого параметра и его заданным значением.
| 
|
| Рис. 75. Пример изменения ошибки во времени | |
Динамической ошибкой будем называть величину, равную наибольшему отклонению регулируемой величины от ее установившегося значения:
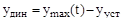 ,
,
Следует отметить, что ошибка (статическая ошибка) является одной из основных количественных характеристик процессов системы.
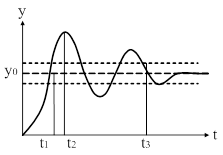
|
| Рис. 76. Иллюстрация оценок быстродействия. |
Быстродействие
В качестве оценок быстродействия можно использовать различные величины, причем все они определяют время от начала процесса до какого-либо характерного значения. С этой целью рассмотрим переходную характеристику системы  , изображенную на рис. 76.
, изображенную на рис. 76.
Оценками быстродействия могут служить:
· 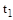 – время от начала процесса до первого момента достижения установившегося значения
– время от начала процесса до первого момента достижения установившегося значения 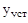 (применимо только для колебательных процессов);
(применимо только для колебательных процессов);
· 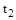 – время достижения первого максимума (также только для колебательных процессов);
– время достижения первого максимума (также только для колебательных процессов);
· 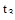 – время от начала переходного процесса до момента, когда отклонение выходной величины становится близким к установившемуся значению с заданной точностью
– время от начала переходного процесса до момента, когда отклонение выходной величины становится близким к установившемуся значению с заданной точностью 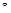 :
: 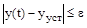 . Обычно в качестве
. Обычно в качестве 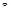 берут 5%-ое отклонение от
берут 5%-ое отклонение от 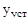 .
.
На практике в качестве оценки быстродействия чаще всего используют величину  , которую обычно обозначают
, которую обычно обозначают 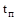 и называют временем переходного процесса.
и называют временем переходного процесса.
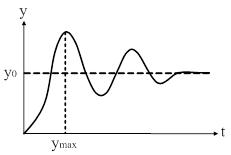
|
| Рис. 77. Иллюстрация оценки перерегулирования. |
Перерегулирование.
Эта количественная оценка характеризует колебательные свойства системы, обозначается буквой 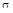 и определяется в процентах относительно установившегося значения (рис. 77) по выражению:
и определяется в процентах относительно установившегося значения (рис. 77) по выражению:
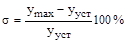 .
.
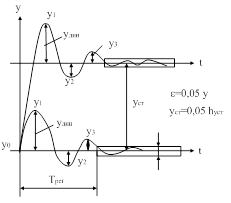
|
| Рис. 78. Показатели качества переходного процесса. |
Очевидно, чем больше перерегулирование 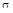 , тем более система склонна к колебаниям.
, тем более система склонна к колебаниям.
Все рассмотренные критерии могут отображены на графике переходного процесса следующим образом ( рис. 78):
Корневые методы.
Как было сказано выше, вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического управления. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая определенные условия на корни характеристического уравнения.
Для оценки быстродействия системы может использоваться понятие степени устойчивости.
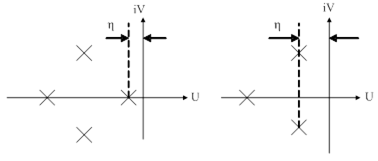
Под степенью устойчивости 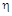 понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 79). Здесь могут быть два случая: когда ближайший корень является вещественным, (рис. 79 а) и когда к мнимой оси ближе всего расположена пара комплексных корней (рис. 79 б).
понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 79). Здесь могут быть два случая: когда ближайший корень является вещественным, (рис. 79 а) и когда к мнимой оси ближе всего расположена пара комплексных корней (рис. 79 б).
|
| |
| а) | б) |
Рис. 79. Расположение корней на комплексной плоскости.

|
| Рис. 80. Иллюстрация к понятию степени устойчивости. |
Корни характеристического уравнения, расположенные ближе всего к мнимой оси, т.е. имеющие наименьшую по абсолютной величине вещественную часть, дают в переходном процессе члены, которые затухают наиболее медленно.
Например, двум разным действительным корням 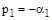 и
и 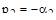 соответствуют две элементарные составляющие свободного движения системы (рис. 80):
соответствуют две элементарные составляющие свободного движения системы (рис. 80):
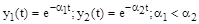 .
.
Очевидно, что чем меньше абсолютное значение корня, тем медленнее затухает составляющая переходного процесса.
Обратимся теперь к оценке запаса устойчивости системы автоматического управления. Склонность системы к колебаниям будет наблюдаться, если в решении характеристического уравнения будут присутствовать комплексные корни вида 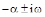 .
.
Степень колебательности m равна минимальному (для всех корней характеристического уравнения системы) модулю отношения действительной и мнимой частей корня, т.е.
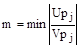
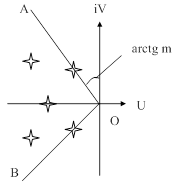
|
| Рис. 81. Иллюстрация к понятию степени колебательности переходного процесса. |
Поясним это определение. Если в плоскости корней характеристического уравнения устойчивой системы провести из начала координат два луча ОА и ОВ (рис. 81) таким образом, чтобы одна пара корней находилась на этих лучах, а все остальные корни лежали слева от них, то тангенс угла, заключенного между этими лучами и мнимой осью, будет равен отношению действительной и мнимой частей корней, лежащих на лучах ОА и ОВ, и являются степенью колебательности 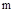 системы, т.к. для других корней это отношение будет больше, чем
системы, т.к. для других корней это отношение будет больше, чем 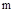 .
.
Колебательность связана с другим корневым показателем запаса устойчивости – с так называемым затуханием. Степень затухания определяется по формуле
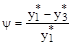 .
.
Между степенью затухания и степенью колебательности существует однозначная зависимость. Действительно, если
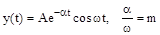 , то
, то
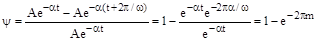 .
.
Очевидно, что степень затухания изменяется в пределах от 0 до 1, а степень колебательности – от 0 до ¥. Наиболее часто используемые значения лежат в пределах от 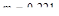 (
( 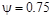 ) до
) до 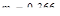 (
( 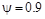 ).
).
Дата: 2019-02-19, просмотров: 377.