Оценить запас устойчивости системы можно также по ее корневому портрету.
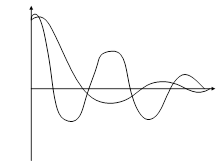
На рис. 3.18 приведены графики переходных процессов двух систем. Видно, что система 2 обладает меньшим запасом устойчивости, поскольку склонность к неустойчивости выражается в большой колебательности процессов.
|
| Рис. 70. Примеры процессов в системах с разным запасом устойчивости |
В свою очередь, характер процессов в системе определяется ее полюсами (корнями), причем колебания будут возникать, если характеристическое уравнение содержит комплексно-сопряженные корни:  ,
,
где вещественная часть (  ) определяет скорость затухания, а мнимая часть корней (
) определяет скорость затухания, а мнимая часть корней (  ) - частоту колебаний.
) - частоту колебаний.
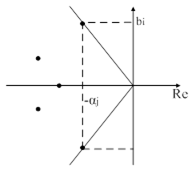
Паре корней с самым «широким» сектором (рис. 70) будет соответствовать составляющая процесса с наибольшими колебаниями, поэтому в качестве оценки запаса устойчивости можно рассматривать отношение 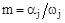 .
.
|
| Рис. 71. Иллюстрация корневых оценок запаса устойчивости системы. |
Отметим, что значение 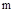 может меняться в диапазоне от 0 до ¥. Чем меньше
может меняться в диапазоне от 0 до ¥. Чем меньше 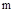 (больше величина мнимой части корня
(больше величина мнимой части корня 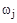 , или меньше вещественная часть), тем ближе будет система к границе устойчивости. В случае, когда
, или меньше вещественная часть), тем ближе будет система к границе устойчивости. В случае, когда 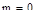 , она находится на границе устойчивости При
, она находится на границе устойчивости При 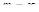 система будет иметь бесконечный запас устойчивости
система будет иметь бесконечный запас устойчивости
Таким образом, корневая оценка запаса устойчивости m характеризует, насколько можно изменять корни характеристического уравнения без потери системой устойчивости.
Обычно такая оценка используется на этапе проектирования, так как ее трудно связать с параметрами реальной системы автоматического управления (коэффициентом усиления, постоянными времени, коэффициентом демпфирования).
Метод D-разбиения
При создании реальной системы управления бывает необходимо знать не только запас устойчивости, который можно оценить с помощью какого-либо критерия, но и всю область устойчивости по параметрам. Этой цели служит метод D-разбиения, позволяющий построить такую область в плоскости одного или двух параметров системы.
Рассмотрим суть метода D-разбиения по одному параметру 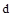 , который входит в характеристическое уравнение системы линейно:
, который входит в характеристическое уравнение системы линейно:
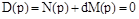
Заменив в этом уравнении  на
на 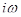 , получим уравнение
, получим уравнение
 ,
,
Решим его относительно 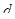 :
:
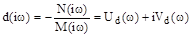 .
.
Получили комплексное представление параметра 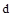 , что позволяет изобразить его в виде вектора на комплексной плоскости. Численное значение частоты определяет положение вектора
, что позволяет изобразить его в виде вектора на комплексной плоскости. Численное значение частоты определяет положение вектора 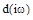 . При изменении
. При изменении 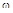 от
от 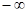 до
до  конец вектора выписывает на комплексной плоскости кривую D-разбиения, представляющую собой границу устойчивости (ее также можно рассматривать как отображение мнимой оси плоскости корней).
конец вектора выписывает на комплексной плоскости кривую D-разбиения, представляющую собой границу устойчивости (ее также можно рассматривать как отображение мнимой оси плоскости корней).

|
| Рис. 72. Пример кривой D-разбиения 1-3 – подобласти с различным распределением корней. |
Кривая D-разбиения симметрична относительно вещественной оси (рис. 72), поэтому достаточно построить ее часть, соответствующую положительным значениям частоты, а вторую половину получить отображением относительно вещественной оси.
Отметим, что эта кривая разбивает комплексную плоскость на несколько подобластей с различным соотношением корней. Для определения области устойчивости необходимо выбрать по одному значению 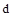 в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при конкретном
в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при конкретном 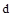 , то она будет устойчива и при всех его значениях из этой области.
, то она будет устойчива и при всех его значениях из этой области.
Обычно в качестве параметра 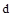 фигурирует реальный параметр системы (коэффициент усиления, постоянная времени, момент инерции и т д.), который может иметь только вещественные значения. Представление его комплексным выражением
фигурирует реальный параметр системы (коэффициент усиления, постоянная времени, момент инерции и т д.), который может иметь только вещественные значения. Представление его комплексным выражением 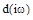 носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.
носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.
Метод D-разбиения можно применять и для построения области устойчивости по двум параметрам 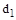 и
и 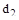 , которые входят линейно в характеристическое уравнение
, которые входят линейно в характеристическое уравнение
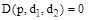
В этом случае уравнение границы устойчивости имеет вид
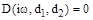
и распадается на два независимых уравнения
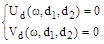
Эти два уравнения параметрически задают кривую D-разбиения. Область устойчивости определяется аналогично случаю одного параметра  .
.
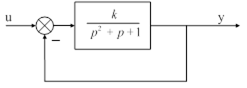
|
| Рис. 73. Структурная схема системы |
Пример.
Определить область устойчивости системы (рис. 73) по коэффициенту усиления.
Определим передаточную функцию замкнутой системы
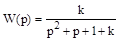
и запишем ее характеристическое уравнение
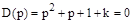 .
.
Здесь  - параметр, по которому строится область устойчивости, поэтому обозначим его через
- параметр, по которому строится область устойчивости, поэтому обозначим его через 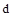 . Решим характеристическое уравнение относительно
. Решим характеристическое уравнение относительно 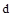 и заменим
и заменим 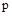 на
на  . В результате получим уравнение для кривой D-разбиения:
. В результате получим уравнение для кривой D-разбиения:
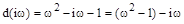
Вычислим значения вещественной и мнимой частей  при положительных значениях частоты и занесем их в таблицу.
при положительных значениях частоты и занесем их в таблицу.
| 0 | 1 | 2 | ¥ | |
| -1 | 0 | 3 | ¥ | |

| 0 | -1 | -2 | -¥ |

|
| Рис. 74. Кривая D-разбиения для исследуемой системы |
Для построения всей кривой D-разбиения полученную половину 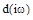 отобразим относительно оси абсцисс (рис. 74).
отобразим относительно оси абсцисс (рис. 74).
Как видим, кривая D-разбиения разделила плоскость параметра на две подобласти (1 и 2). Выбираем по одному вещественному значению 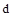 в каждой из них и оцениваем устойчивость.
в каждой из них и оцениваем устойчивость.
Исследуемая система имеет второй порядок, поэтому необходимым и достаточным условием ее устойчивости является положительность всех коэффициентов характеристического уравнения. Следовательно, первая область есть область устойчивости (  ), а вторая - неустойчивости.
), а вторая - неустойчивости.
Дата: 2019-02-19, просмотров: 350.