Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинство в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.
Принцип аргумента.
Запишем характеристический полином САУ в виде
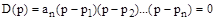
Его корни 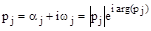 ,
,
где 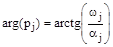 ;
; 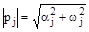 .
.
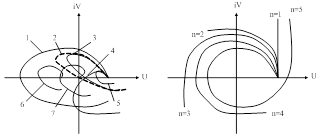
Каждый корень можно изобразить вектором на комплексной плоскости (рис. 57 а), тогда разность  изобразится разностью векторов (рис. 57 б), где
изобразится разностью векторов (рис. 57 б), где 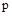 - любое число.
- любое число.
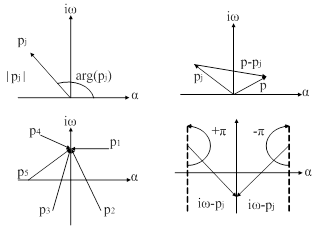
Рис. 57. Иллюстрация к принципу аргумента.
Если менять значение 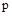 произвольным образом, то конец вектора
произвольным образом, то конец вектора 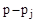 будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как
будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как 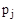 - это конкретное неизменное значение.
- это конкретное неизменное значение.
В частном случае, если на вход системы подавать гармонические колебания с различной частотой 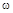 , то
, то 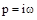 , а характеристический полином принимает вид:
, а характеристический полином принимает вид:
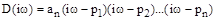
При этом концы векторов 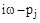 будут находиться на мнимой оси (рис. 57). Если менять
будут находиться на мнимой оси (рис. 57). Если менять 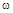 от -¥ до ¥, то каждый вектор
от -¥ до ¥, то каждый вектор 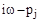 будет поворачиваться относительно своего начала
будет поворачиваться относительно своего начала 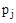 на угол
на угол 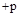 для левых и
для левых и 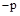 для правых корней (рис. 57).
для правых корней (рис. 57).
Характеристический полином можно представить в виде
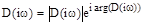 ,
,
uде  ;
;
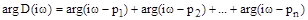
Пусть из 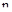 корней
корней 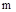 - правые, а
- правые, а 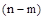 - левые, тогда угол поворота вектора
- левые, тогда угол поворота вектора 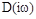 при изменении
при изменении  от -¥ до ¥ равен
от -¥ до ¥ равен
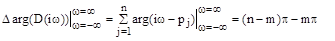
или при изменении 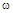 от 0 до ¥ получаем
от 0 до ¥ получаем
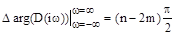
Отсюда вытекает правило: изменение аргумента вектора р при изменении частоты 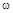 от -¥ до ¥ равно разности между числом левых и правых корней характеристического уравнения, умноженному на p, а при изменении частоты
от -¥ до ¥ равно разности между числом левых и правых корней характеристического уравнения, умноженному на p, а при изменении частоты 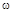 от 0 до ¥ эта разность умножается на p/2.
от 0 до ¥ эта разность умножается на p/2.
Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.
Критерий Михайлова.
Критерий был сформулирован А.В. Михайловым в 1938 г., он базируется на принципе аргумента функции комплексного переменного.
Также, как и алгебраический критерий, критерий Михайлова применяется в тех случаях, когда задано дифференциальное уравнение системы. В общем виде оно записывается следующим образом
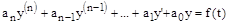 .
.
Для анализа устойчивости системы предлагается исследовать характеристический комплекс 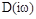 , который получается из характеристического полинома
, который получается из характеристического полинома
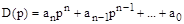
заменой  на
на 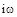 и имеет вид:
и имеет вид:
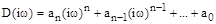 . (6)
. (6)
Выделим вещественную и мнимую части:
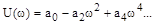 ,
, 
При конкретном численном значении частоты 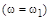 характеристический комплекс (6) представляет собой комплексное число
характеристический комплекс (6) представляет собой комплексное число 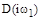 , которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой
, которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой 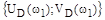 .
.
При изменении частоты 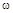 от 0 до ¥ конец вектора
от 0 до ¥ конец вектора  выписывает на комплексной плоскости некоторую кривую, которая называется годографом Михайлова. Причем начинается годограф, как следует из соотношения (6), в точке
выписывает на комплексной плоскости некоторую кривую, которая называется годографом Михайлова. Причем начинается годограф, как следует из соотношения (6), в точке 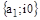 .
.
Формулировка критерия.
Замкнутая система устойчива, если годограф 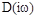 начинаясь при w = 0 на действительной положительной полуоси, огибает с рстом
начинаясь при w = 0 на действительной положительной полуоси, огибает с рстом 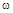 от 0 до ¥ против часовой стрелки начало координат, проходя последовательно в положительном направлении
от 0 до ¥ против часовой стрелки начало координат, проходя последовательно в положительном направлении 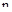 квадрантов, где
квадрантов, где 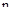 – порядок системы. При этом, изменение аргумента
– порядок системы. При этом, изменение аргумента 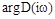 равно
равно 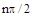 . В общем случае приращение аргумента составляет
. В общем случае приращение аргумента составляет 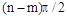 , где
, где 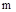 – число правых корней, но для устойчивой САУ
– число правых корней, но для устойчивой САУ 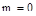 .
.
|
| |
| а) | б) |
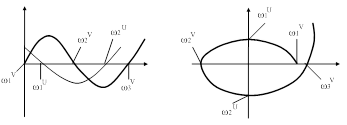
Рис. 58. Примеры годографов вектора Михайлова.
На рис. 58 а годограф 1 относится к устойчивой САУ, годографы 3, 4, 5, 6, 7 – к неустойчивым системам.
Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат (кривая 2). В этом случае существует значение  , при котором
, при котором 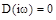 , т.е. характеристическое уравнение системы имеет пару комплексно сопряженных мнимых корней. Последнее означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате чего годограф
, т.е. характеристическое уравнение системы имеет пару комплексно сопряженных мнимых корней. Последнее означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате чего годограф 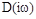 отойдет влево, или вниз от начала координат, делает систему устойчивой или нет.
отойдет влево, или вниз от начала координат, делает систему устойчивой или нет.
Следствие критерия Михайлова.
Система устойчива, если годограф Михайлова последовательно пересекает вещественную и мнимую оси, начинаясь на вещественной оси. Следовательно, необходимо и достаточно, чтобы точки пересечения годографа Михайлова положительной и отрицательной осей чередовались между собой.
На рис. 58 б приведены годографы устойчивых систем разных порядков до  .
.
При практическом построении годографа 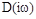 прежде всего находят точки его пересечения с координатными осями. Для этого, определив из уравнения
прежде всего находят точки его пересечения с координатными осями. Для этого, определив из уравнения 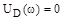 значения частот, соответствующие точкам пересечения годографа
значения частот, соответствующие точкам пересечения годографа  с мнимой осью, подставляют их в выражение
с мнимой осью, подставляют их в выражение  . В результате получают соответствующие ординаты. Аналогично находят точки пересечения
. В результате получают соответствующие ординаты. Аналогично находят точки пересечения  с действительной осью, приравнивая нулю мнимую часть
с действительной осью, приравнивая нулю мнимую часть 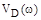 и подставляя затем найденные при этом значения
и подставляя затем найденные при этом значения 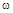 в выражение для
в выражение для 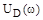 .
.
После того, как найдены значения частоты, при которых годограф  пересекает оси координат, т.е. найдены нули
пересекает оси координат, т.е. найдены нули 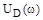 и
и 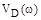 для суждения об устойчивости системы нет необходимости строить сам годограф.
для суждения об устойчивости системы нет необходимости строить сам годограф.
Пример 1.

Характеристическое уравнение для данной системы:
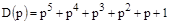
Вектор Михайлова получим из характеристического уравнения заменой  на
на 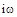 :
:
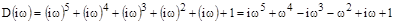 ;
;
 ,
, 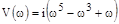 .
.
Перед построением всего годографа 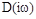 определим точки его пересечения с действительной и мнимой осями, т.е. найдем действительные и мнимые корни полиномов
определим точки его пересечения с действительной и мнимой осями, т.е. найдем действительные и мнимые корни полиномов 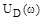 и
и 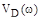 .
.
Найдем точку пересечения с мнимой осью 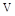 :
:
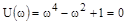

|
| Рис. 59. Иллюстрация к примеру. |
Это уравнение действительной корней не имеет, стало быть, годограф Михайлова не пересекает мнимую часть (рис. 59).
Дальнейший расчет можно не проводить, т.к. из первого заключения ясно, что система неустойчива. Действительно, по критерию Михайлова 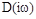 устойчивой системы 5-го порядка при изменении
устойчивой системы 5-го порядка при изменении 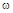 от 0 до ¥ должен пройти 5 квадрантов, начиная с 1-го, т.е. пересечь мнимую ось 2 раза.
от 0 до ¥ должен пройти 5 квадрантов, начиная с 1-го, т.е. пересечь мнимую ось 2 раза.
Пример 2. 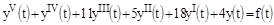
Характеристическое уравнение:
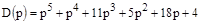 .
.
Вектор Михайлова:
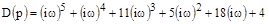
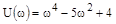 ;
;  .
.
Определим корни  и
и 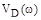 .
.
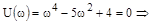
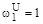 ,
, 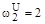
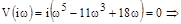
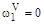 ,
, 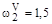
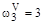 .
.
Расположив найденные корни на числовой оси (рис. 3.8 а), видим, что корни 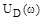 и
и 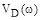 чередуются друг с другом, т.е. «критерий перемежаемости» выполняется. Полное исследование зависимости
чередуются друг с другом, т.е. «критерий перемежаемости» выполняется. Полное исследование зависимости  и
и 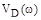 позволяет построить их графики и годограф
позволяет построить их графики и годограф  . Из годографа видно, что система устойчива.
. Из годографа видно, что система устойчива.
|
| |
| а) | б) |
Рис. 60. Построение годографа вектора Михайлова.
Дата: 2019-02-19, просмотров: 401.