Поведение системы в любой момент времени может быть описано дифференциальным уравнением. В соответствии с классическим методом решение дифференциального уравнения ищется в виде:

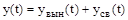
Здесь 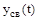 - общее решение однородного дифференциального уравнения, то есть уравнения с нулевой правой частью:

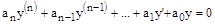
Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения.

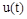 - частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие . Поэтому вторая составляющая общего решения называется вынужденный. Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.

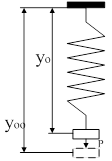
Рис. 55. Вынужденные колебания в пружине под действием силы .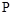

Можно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением (рис. 55). Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени 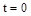 подвесить к пружине груз, то на свободные колебания наложится внешняя сила . После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей 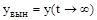. Если внешнее воздействие само будет изменяться по синусоидальному закону 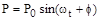, то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то есть .

Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени 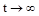. Свободная составляющая представляет собой сумму из  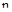отдельных составляющих 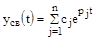, где 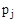 – корни характеристического уравнения

.

Корни могут быть либо вещественными 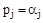, либо попарно комплексно сопряженными 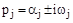. Постоянные интегрирования 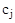определяются исходя из начальных и конечных условий, подставляя в общее решение значения 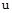, y и их производные в моменты времен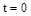и  и .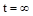

В общем случае, в зависимости от величины и знака действительной части возможны следующие варианты расположения корней на комплексной плоскости:

1) Корни расположены в левой полуплоскости («левые» корни):

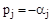 тогда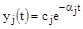  

 ® .

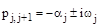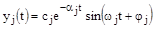2) Корни расположены в правой полуплоскости («правые» корни):

 ® ;

 ® .

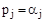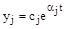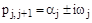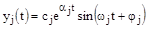3) Корни лежат на мнимой оси:

 ® .

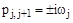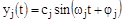 Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая 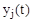, каждому положительному - экспоненциально расходящаяся, каждому нулевому корню соответствует 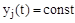. Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой 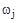, при положительной вещественной части - расходящиеся колебания, при нулевой - незатухающие (рис.56).

Так как после снятия возмущения , то устойчивость системы определяется только характером свободной составляющей 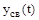. Поэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанного в отклонениях, должна стремиться к нулю, то есть затухать.

Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю, а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости.

Рис. 56. Элементарные составляющие переходного процесса.

Так как после снятия возмущения 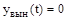, то устойчивость системы определяется только характером свободной составляющей 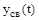. Поэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанного в отклонениях, должна стремиться к нулю, то есть затухать.

Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю, а остальные левые, то система находится на границе апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости.

Теоремы Ляпунова А.М.

Реальные системы являются, как правило, нелинейными.

Судить об устойчивости реальных систем можно по корням характеристического уравнения линеаризованных систем с помощью следующих теорем Ляпунова А.М.

Теорема 1: Если корни характеристического уравнения линеаризованной системы имеют отрицательную вещественную часть, то исходная реальная система устойчива.

Теорема 2: Если среди корней характеристического уравнения линеаризованной системы имеется хотя бы один корень с положительной вещественной частью, а остальные корни имеют отрицательную вещественную часть, то исходная реальная система неустойчива.

Теорема 3: Если среди коней характеристического уравнения линеаризованной системы имеется хотя бы один нулевой корень или одна пара чисто мнимых корней, то судить об устойчивости реальной системы нельзя, необходимо дальнейшее исследование.

Однако, на практике САУ рассчитываются с определенным запасом устойчивости. Поэтому в узкую область разделяющую линеаризованную систему от границы устойчивости, входит и граница устойчивости реальных систем. Поэтому можно сказать что в этом случае реальная система также будет находится на границе устойчивости.

Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости. Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и частотные (основаны на исследовании частотных характеристик).