Рис. 61. Структурная схема замкнутой системы.

Критерий Найквиста позволяет определить устойчивость системы с отрицательной обратной связью (так называемой замкнутой системы) по экспериментально снятой или полученной на основе передаточной функции амплитудно-фазовой частотной характеристики разомкнутой системы.

Рассмотрим этот критерий для системы с единичной обратной связью (рис. 3.9).

Здесь 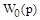 – передаточная функция устойчивой разомкнутой системы, которая в общем случае имеет вид

, ,

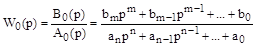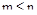где 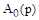 – характеристический полином разомкнутой системы.

Определим передаточную функцию системы, изображенной на рис. 3.9:

,

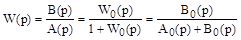где 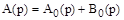- характеристический полином замкнутой системы.

Предварительно введем вспомогательную передаточную функцию

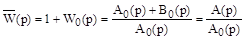.                      (7)

Как видим, ее числитель представляет собой характеристический полином замкнутой системы, а знаменатель – характеристический полином разомкнутой системы. Причем, во вспомогательной передаточной функции числителя и знаменателя имеют одинаковый порядок, равный .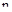

Получим выражение для вспомогательной частотной характеристики, заменив в выражении (7) 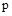 на :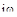

.

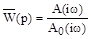Рассмотрим теперь результирующий угол поворота вектора 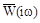при изменении  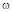от 0 до ¥, используя принцип аргумента.

Если замкнутая система устойчива, то общее приращение аргумента числителя будет равно 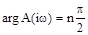. При устойчивой разомкнутой системе приращение аргумента знаменателя составит: 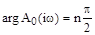. Результирующий угол поворота вектора 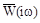будет равен разности этих аргументов, т.е.:

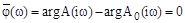.                          (8)

Таким образом, для устойчивости замкнутой системы при устойчивой разомкнутой должно выполняться соотношение (8). Это свойство имеет простую геометрическую интерпретацию: вспомогательная частотная характеристики не должна охватывать начало координат комплексной плоскости. Так как 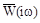отличается от  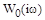на единицу, можно строить АФХ разомкнутой системы, что значительно проще.

Формулировка критерия Найквиста.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении 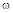 от 0 до ¥ не охватывала точку с координатами .

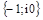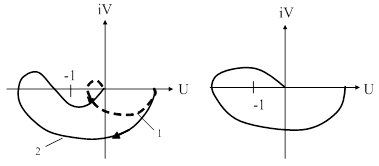
Примеры расположения частотных характеристик, соответствующих устойчивой и неустойчивой замкнутым системам, представлены на рис. 3.10.

Рис. 62. Иллюстрация критерия Найквиста: а) – устойчивые; б) – неустойчивые.

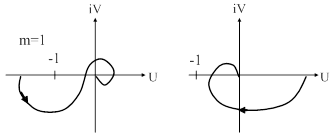
Разомкнутая система может быть неустойчива, однако это не означает, что неустойчивой будет и замкнутая система. В этой ситуации следует использовать видоизмененную формулировку критерия Найквиста: замкнутая система будет устойчива тогда и только тогда, когда амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении  от 0 до ¥ охватывает точку с координатами 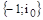 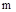раз, где  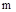– число корней характеристического уравнения разомкнутой системы с положительной вещественной частью. Под охватом точки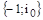 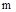 раз понимается поворот вектора АФХ разомкнутой системы на угол mp при изменении  от 0 до ¥ (рис. 63).

Рис. 63. Иллюстрация критерия Найквиста а) – устойчивые; б) – неустойчивые.

Пример 1.

Определить будет ли устойчива система с передаточными функциями: ; .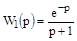

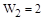В решении задачи можно выделить 3 основных этапа.

1) Исследование устойчивости разомкнутой системы (по критерию Гурвица или Михайлова)

2) построение АФХ разомкнутой системы

3) оценка взаимного расположения годографа и точки с координатами .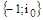

Для определения устойчивости разомкнутой системы в данном примере не требуется применять каких-либо критериев, т.к. система состоит из последовательно соединенных элементарных, устойчивых звеньев: чистого запаздывания, апериодического I-го порядка и усилительного звена – и, следовательно, будет устойчивой. Ее передаточная функция

.

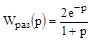Выведем формулы и построим графики частотных характеристик разомкнутой системы:

; ; .

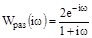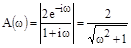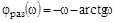Рис. 64. Частотные характеристики разомкнутой системы.

Из графиков частотных характеристик видно, что годограф 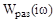 при увеличении  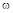от 0 до ¥ пересекает отрицательную ветвь действительной оси бесконечное число раз. Т.к. модуль АФХ при этом монотонно убывает, то для анализа устойчивости достаточно найти первую точку пересечения, соответствующую наименьшей частоте .

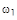Значение 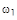 найдем из уравнения

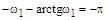
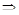
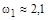
Величина модуля вектора 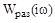 при частоте :

.

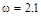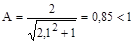Т.к. модуль АФХ при 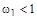, годограф АФХ не охватывает точку 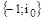, следовательно,  замкнутая система будет устойчивой.