Рис. 82. Иллюстрация к оценке переходного процесса по АЧХ системы.

Эти критерии позволяют судить о качестве переходных процессов по частотным характеристикам системы. Для ряда систем качество переходных процессов может быть определено по одной амплитудной характеристике замкнутой системы 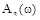. По АЧХ можно оценить колебательность и длительность переходной характеристики системы.

Колебательность определяется по величине максимума характеристики, который поэтому называется показателем колебательности:

 .

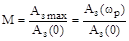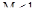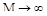При  переходная характеристика системы неколебательна (штриховая линия на рис. 82). Чем больше , тем больше колебательность. При  колебательность возрастает до получения незатухающих колебаний, соответствующих нахождению системы на границе устойчивости.

Оптимальным обычно считается 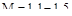. При этом переходная характеристика имеет слабую колебательность с частотой, близкой к частоте  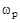резонансного пика АЧХ.

Длительность 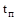 переходной характеристики определяется шириной частотной характеристики . При этом зависимость здесь такая: чем шире частотная характеристика системы, тем короче ее переходная характеристика, т.е. тем меньше .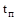

Так в случае апериодического звена с передаточной функцией 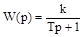 ширина АЧХ обратно пропорциональна постоянной времени звена 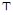. В то же время длительность переходной характеристики 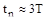, т.е. прямо пропорциональна .

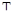В первом приближении длительность переходной характеристики может быть оценена по величине резонансной частоты 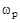. Т.к. частота колебаний переходной характеристики премерно равна 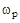, время  достижения первого максимума переходной характеристики близко половине периода колебаний этой частоты, т.е.

.

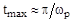Если при этом предположить, что переходная характеристика в течение 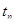 имеет 1-2 колебания, то

.

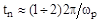3.7.5. Интегральные оценки.

Интегральные критерии в отличие от прямых показателей, дают обобщенную оценку качества переходных процессов.

Рис. 83. Линейный интегральный критерий.

Одно из достоинств интегральных критериев качества состоит в том, что для их вычисления не требуется построения самого переходного процесса, которое часто сопряжено с определенными трудностями. Оценка интегрального критерия может производиться по другим характеристикам, которыми обычно располагают при проектировании САР. Используют несколько видов интегральных критериев.

1) Линейный интегральный критерий качества (рис. 83):

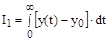Геометрически этот критерий характеризует площадь, заключенную между кривой переходного процесса и осью времени. Очевидно, что увеличение динамической ошибки и времени регулирования приводит к росту .

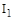2) Модульный интегральный критерий качества вычисляется по формулам:

,

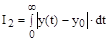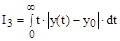
и применяются для оценки колебательных процессов.

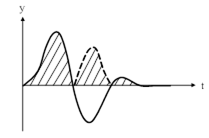
Рис. 84. Модульный интегральный критерий.

Особый интерес представляет модифицированный модульный критерий 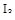, в котором каждая ордината переходного процесса  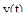входит со своим весовым коэффициентом, равным времени .

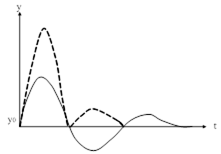
Рис. 85. Интегральный квадратичный критерий.

Это означает, что чем дольше продолжается процесс, тем больше значение этого критерия при одних и тех же значениях суммы модулей самих ординат. Следовательно, если для заданного объекта подобрать переходный процесс, соответствующий минимальному значению критерия 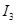, то время этого процесса будет меньше, чем у процесса с минимальным значением .

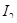3) Интегральный квадратичный критерий:

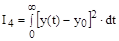
Это наиболее распространенный критерий качества для колебательных процессов. Специфическая особенность квадратичного критерия в том, что каждая ордината процесса входит в него с весом, равным самой ординате. Это означает, что с наибольшим весом в него входит динамическая ошибка, а конечный участок процесса, когда 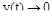, оказывает на критерий незначительное влияние. Поэтому переходный процесс, соответствующий минимальному значению квадратичного критерия, отличается малыми динамическими ошибками и относительно большим временем затухания.

Интегральный квадратичный критерий, также как и линейный, можно вычислить без построения переходного процесса по частотной характеристике системы.

4) Обобщенный интегральный квадратичный критерий отличается от обычного квадратичного критерия тем, что помимо ординат переходного процесса в нем учитываются и производные от :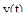

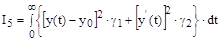
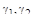– весовые коэффициенты, определяющие относительный вес составляющих интеграла  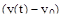и .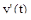

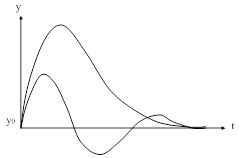
Рис. 86. Переходные процессы, соответствующие одному значению I4.

Каким же образом используются все рассмотренные выше показатели и критерии качества? Прежде всего необходимо отметить, что обеспечить наилучшие значения одновременно всех показателей невозможно, т.к. часть из них противоречат друг другу. Например, повышение степени устойчивости и степени колебательности приводит к снижению скорости регулирования, а это влечет за собой увеличение динамической ошибки.

С другой стороны, при использовании какого-либо одного критерия можно получить множество переходных процессов, удовлетворяющих этому критерию. Например, на рис. 86. изображены два процесса для одного объекта, имеющие одинаковое значение 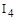, но существенно отличающиеся друг от друга по динамическим ошибкам, времени регулирования и степени затухания.

Поэтому при расчете систем регулирования обычно используют два показателя качества: для одного из них, называемого критерием, добиваются наилучшего (т.е. минимального или максимального) значения, для другого вводят ограничение в виде неравенства.

Например, можно стремиться к минимальному значению динамической ошибки при условии, что степень затухания будет не ниже заданной. Возможна и другая постановка задачи: минимизировать время переходного процесса при условии, что динамическая ошибка будет меньше допустимой.

Заметим, что если в первом случае динамическая ошибка была выбрана в качестве критерия, то во втором примере она является ограничением. Однако, наиболее часто за критерии качества принимают интегральные критерии, которые требуется минимизировать при ограничении на степень затухания или степень колебательности.