Необходимое условие устойчивости.

Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде:

,

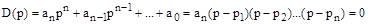где 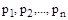 – корни этого уравнения.

Если система устойчива, значит все корни левые, то есть вещественные части всех корней отрицательны, что можно записать как 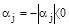. Подставим их в уравнение:

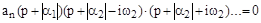
Перемножая комплексно сопряженные выражения, получим:

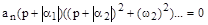
После раскрытия скобок должно получиться выражение, аналогичное характеристическому уравнению, где все коэффициенты 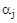 будут положительными. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: 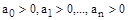. В дальнейшем будем рассматривать только уравнения, где 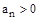. В противном случае уравнение дополнительно умножается на -1.

Рассмотренное условие является необходимым, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.

Критерий Гурвица.

Пусть система описывается дифференциальным уравнением 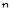-го порядка (нумерация коэффициентов здесь проводится в обратном порядке по сравнению со стандартным дифференциальным уравнением)

Составим из коэффициентов этого уравнения матрицу следующего вида

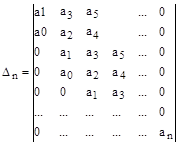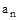Матрица составляется по следующему правилу: в главной диагонали записывается подряд все коэффициенты, начиная с  по . Затем заполняются столбцы таким образом, чтобы над диагональю располагались подряд коэффициенты с возрастающими номерами, а под диагональю - с убывающими номерами. Свободные элементы матрицы заполняются нулями. В результате все нечетные строки содержат коэффициенты с нечетными номерами, а четные - только с четными, причем каждая следующая пара строк смещена по отношению к предыдущей на один столбец вправо.

Для определителя 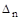запишем диагональные миноры, которые называются определителями Гурвица.

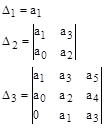
В соответствии с критерием Гурвица, для того чтобы линейная система была устойчивой, необходимо и достаточно, чтобы все определители были положительными (при условии, что ).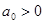

Если хотя бы один определитель отрицательный, система будет не устойчива. Если один определитель равен нулю, а все остальные положительны, система находится на границе устойчивости.

Исходя из этого критерия, посмотрим, какие условия накладываются на коэффициенты дифференциальных уравнений I-го, II-го и III-го порядка.

1)

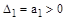
2)

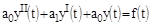
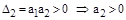
3)

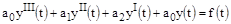
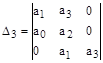
Таким образом, для систем I-го и II-го порядков необходимое условие устойчивости - положительность всех коэффициентов дифференциального уравнения – оказывается и достаточным. Для систем более высокого порядка этого условия недостаточно и на коэффициенты накладываются дополнительные ограничения. В частности, для систем III-го порядка произведение средних коэффициентов должно быть больше произведение крайних.

Пример 1.

, , , ,

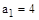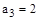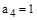
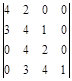
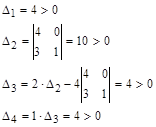
Поскольку все определители Гурвица больше нуля, система устойчива.

Пример 2.

, , , ,

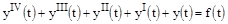
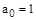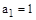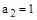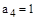
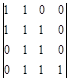
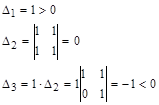
Система неустойчива, т.к. третий определитель отрицательный.