Состояние каждой системы описывается дифференциальными уравнениями первого порядка относительно каждой переменной состояния. Эти уравнения в общем случае имеют следующий вид:

,

,

.

.

,

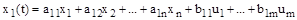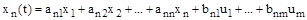где 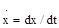. Эту же систему дифференциальных уравнений можно записать в матричной форме:

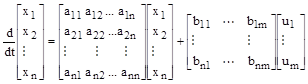
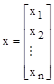Матрица –столбец, состоящая из переменных состояния, называется вектором состояния и имеет вид:

Вектор входных сигналов обозначается как u. Тогда систему можно описать в компактном виде дифференциальным уравнением состояния

                                                  (4)

Это уравнение часто называют просто уравнением состояния. Матрица 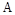 является квадратной размерности , а матрица 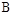 имеет размерность 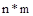. Уравнение состояния связывает скорость изменения состояния системы с самим состоянием и входными сигналами. В общем случае выходные сигналы линейной системы связаны с переменными состояния и выходными сигналами уравнения выхода

,

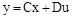где 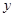– совокупность выходных сигналов, представленных в виде вектора –столбца.

Решение дифференциального уравнения состояния (*) можно получить точно также, как решается скалярное дифференциальное уравнение первого порядка. Рассмотрим уравнение

,

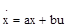где 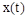 и 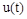 – скалярные функции времени. Решение будем искать в виде экспоненты . Преобразуем это уравнение по Лапласу, получим:

,

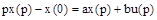откуда

.

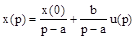Обратное преобразование Лапласа дает искомое решение:

.

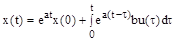Аналогично получается и решение дифференциального уравнения состояния. Прежде всего, введем в рассмотрение матричную экспоненциальную функцию, представив ее в виде ряда

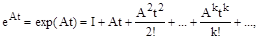
который сходится для всех конечных  и любой 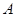. 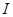– единичная матрица. Тогда решение уравнения состояния будет иметь вид:

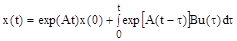.         (5)

Решение этого уравнения можно получить, применив преобразование Лапласа к уравнению состояния (4) и сгруппировав члены. В результате получим:

,

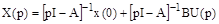где можно ввести обозначение 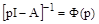, что является преобразованием Лапласа функции 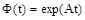. Применив к последней формуле обратное преобразование Лапласа и учитывая, что второе слагаемое в правой части содержит произведение 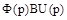, мы получим решение (5). матричная экспоненциальная функция 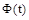описывает свободное движение системы и называется фундаментальной матрицей или переходной матрицей состояния.

Таким образом, решение (5) можно записать в виде:

.

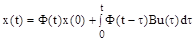АНАЛИЗ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ УПРАВЛЕНИЯ

Анализ устойчивости

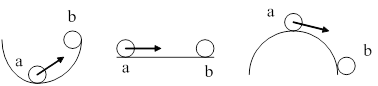
Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой. Существуют также нейтральные системы, которые после снятия возмущения приходят в состояние равновесия, отличное от исходного. Простейшие модели таких систем показаны на рис. 53.

Рис. 53. Модели устойчивой (а), нейтральной (б) и неустойчивой (в) систем.

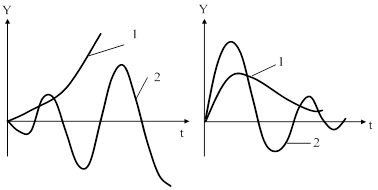
Рис. 54. Графики переходных процессов в неустойчивой (рис. а) и устойчивой (рис. б) системах.

На рис. 54 показаны типичные кривые переходных процессов. Если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. Этот процесс может быть апериодическим (рис. а – кривая 1) или колебательным (кривая 2).

Апериодический расходящийся процесс может, например, возникнуть в САУ, если в ее управляющем устройстве ошибочно переключить полярность воздействия на объект, в результате чего управляющее устройство будет осуществлять не отрицательную, а положительную обратную связь вокруг объекта. При этом управляющее устройство будет не устранять отклонение 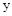, а действовать в обратном направлении.

Колебательный расходящийся процесс может наступить, например, при неограниченном увеличении коэффициента передачи системы, вследствие чего управляющее устройство станет излишне энергично воздействовать на объект, стремясь ликвидировать первоначально возникшее отклонение 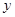. В этом случае, при каждом очередном возврате  к нулю под действием управляющего устройства, кривая 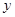 будет пересекать ось абсцисс все с большей скоростью и процесс в целом будет расходящимся.

В случае устойчивой системы (рис. б) переходный процесс, вызванный каким-либо воздействием, со временем затухает апериодически (кривая 1) или колебательно (кривая 2) и система вновь возвращается в установившееся состояние.

Т.о. устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими.

Общее условие устойчивости.