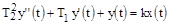 ,
,
где 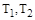 - постоянные времени,
- постоянные времени, 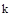 – коэффициент усиления.
– коэффициент усиления.
Характеристическое уравнение запишется в виде:
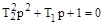 .
.
Корни этого уравнения 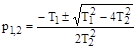 будут комплексными при условии
будут комплексными при условии 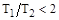 . Если это неравенство не выполняется, корни этого уравнения будут действительными, что соответствует случаю апериодического звена II-го порядка, для которого
. Если это неравенство не выполняется, корни этого уравнения будут действительными, что соответствует случаю апериодического звена II-го порядка, для которого 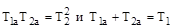 .
.
Уравнение установившегося статического режима этого звена имеет тот же вид, что и для усилительного и апериодического звеньев: 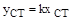
Передаточная функция: 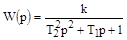
Частотные характеристики (рис. 30.)
АФХ: 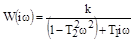 ; АЧХ:
; АЧХ: 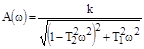 ;
;
ФЧХ: 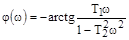 .
.
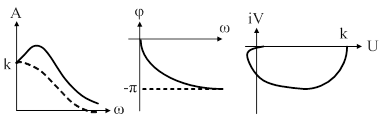
Рис. 30. Частотные характеристики колебательного звена.
Как видно из формулы для АЧХ при малых значениях 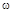 , когда
, когда 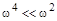 , наблюдается некоторое увеличение
, наблюдается некоторое увеличение 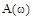 по сравнению с апериодическим звеном (показана пунктиром), причем при малых значениях отношения
по сравнению с апериодическим звеном (показана пунктиром), причем при малых значениях отношения 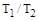 на графике
на графике 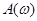 появляется максимум, в предельном случае при
появляется максимум, в предельном случае при 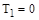 , на частоте
, на частоте 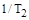 получается резонансный пик (консервативное звено).
получается резонансный пик (консервативное звено).
|
| |
| а) | б) |
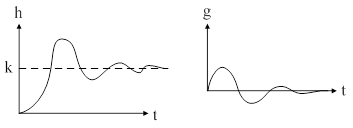
Рис. 31. Переходные функции колебательного звена: а) – кривая разгона; б) – импульсная переходная функция.
Уравнение кривой разгона в операторной форме имеет вид:
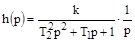
По таблицам оригиналов находим:
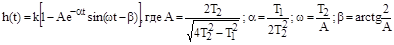
По экспериментально снятой кривой разгона (переходной функции) можно найти параметры 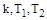 .
.
|
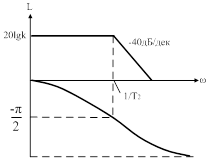
| Рис. 32. Логарифмическая характеристика колебательного звена |
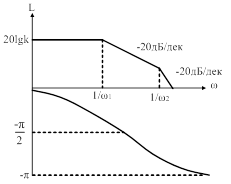
Асимптотическая л.а.х. представляет собой ломаную линию, состоящую из двух асимптот, к которым стремится л.а.х. при 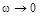 и при
и при 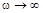 . Одна асимптота – линия, параллельная оси абсцисс и отстоящая от нее на расстояние
. Одна асимптота – линия, параллельная оси абсцисс и отстоящая от нее на расстояние 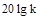 , Другая асимптота имеет наклон -40 дБ/дек. Точка пересечения соответствует частоте
, Другая асимптота имеет наклон -40 дБ/дек. Точка пересечения соответствует частоте 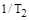 .
.
Уравнение первой асимптоты получается из уравнения для л.а.х.:
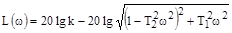 .
.
При 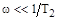 ,
, 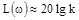 .
.
Уравнение второй асимптоты соответствует 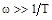 .
.
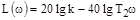 .
.
Из последнего выражения следует, что при увеличении частоты на декаду  снижается на 40 дБ, что и определяет указанный выше наклон – 40дБ/дек.
снижается на 40 дБ, что и определяет указанный выше наклон – 40дБ/дек.
Введем условное обозначение 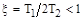
При 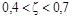 расхождение между асимптотической и истинной л.а.х. не превышает 3дБ, как и в случае апериодического звена. Поэтому для звеньев с таким значением
расхождение между асимптотической и истинной л.а.х. не превышает 3дБ, как и в случае апериодического звена. Поэтому для звеньев с таким значением 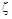 можно пользоваться асимптотической л.а.х. Фазовая частотная характеристика представлена ниже, вместе с л.а.х
можно пользоваться асимптотической л.а.х. Фазовая частотная характеристика представлена ниже, вместе с л.а.х
Примеры колебательного звена: электрический резонансный контур RLC; электрический двигатель при достаточно большой постоянной времени якоря; упругие механические передачи.
4. Статическое звено второго порядка (апериодическое II -го порядка).
Такое звено описывается аналогичным уравнением, как и колебательное, только здесь 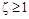 . Обобщенное уравнение второго порядка имеет вид:
. Обобщенное уравнение второго порядка имеет вид:
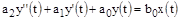 .
.
Апериодическое звено II-го порядка можно представить как цепочку последовательно соединенных двух звеньев I порядка, с постоянными времени 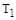 и
и 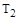 и коэффициентами усиления
и коэффициентами усиления 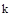 и 1.
и 1.
Общая передаточная функция цепочки будет равна:
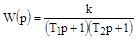 .
.
Следовательно, уравнение звена в операторской форме запишется в виде:
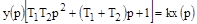 ,
,
откуда получается дифференциальное уравнение:
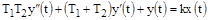 .
.
Частотные характеристики апериодического звена II-го порядка (рис. 33):
АФХ: 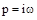
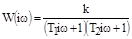 ; АЧХ:
; АЧХ: 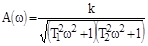
ФЧХ: 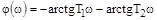
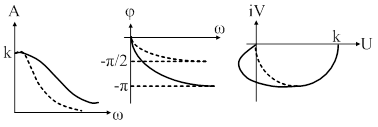
Рис. 33. Частотные характеристики апериодического звена II-го порядка
На рис. 33 пунктиром показаны частотные характеристики звена I-го порядка с коэффициентом усиления  и постоянной времени
и постоянной времени 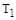 . Как видно из рисунка, добавление другого звена I-го порядка уменьшает значение модуля АФХ и увеличивает отставание по фазе для каждой частоты по сравнению с одноемкостным звеном.
. Как видно из рисунка, добавление другого звена I-го порядка уменьшает значение модуля АФХ и увеличивает отставание по фазе для каждой частоты по сравнению с одноемкостным звеном.
Уравнение кривой разгона (переходной функции) в операторной форме запишется в виде:
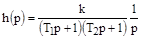 .
.
Оригинал этой функции имеет вид:
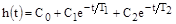 ,
, 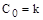 ;
; 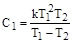 ;
; 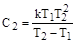 .
.
|
| |
| а) | б) |
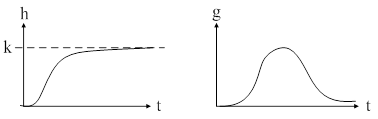
| Рис. 34. Переходные характеристики апериодического звена II-го порядка: а) - кривые разгона; б) – импульсная переходная функция. | |
|
Рис. 35. Логарифмическая характеристика апериодического звена II-го порядка. ( 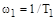 ; ; 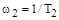 ). ).
|
График 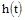 представляет собой апериодическую кривую, имеющую точку перегиба и асимптотически стремящуюся к
представляет собой апериодическую кривую, имеющую точку перегиба и асимптотически стремящуюся к  (рис. 34).
(рис. 34).
Уравнение импульсной переходной функции получим из формулы для 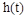 путем дифференцирования:
путем дифференцирования:
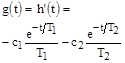
Логарифмическая характеристика (рис. 35):
Интегрирующие звенья.
Дата: 2019-02-19, просмотров: 480.