Линейное дифференциальное уравнение апериодического звена:

,

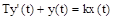где 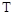 – постоянная времени звена;  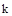– коэффициент усиления.

Примером такого звена может служить любая цепочка, включающая сопротивление и емкость независимо от их физической природы.

Передаточная функция получается из уравнения звена:

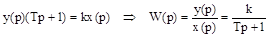
Частотные характеристики описываются формулами:

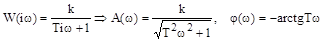
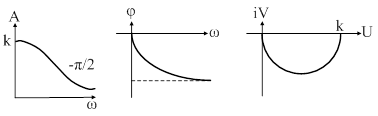
Рис. 27.  Частотные характеристики апериодического звена первого порядка.

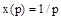Уравнение кривой разгона получается как решение дифференциального уравнения апериодического звена при нулевых начальных условиях и  или из уравнения передаточной функции апериодического звена при . Тогда

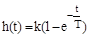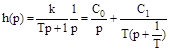, или , где .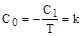

Весовая функция находится как производная от кривой разгона

Соответствующие характеристики представлены на рис. 28.

Рис. 28. Переходные характеристики апериодического звена первого порядка.

Если эти характеристики получены экспериментально, по ним можно определить значения 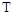 и , как показано на рисунках, и, т.о. получить уравнение звена.

Величина постоянной времени 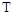 определяет инерционность звена: чем она больше, тем длительнее переходный процесс в звене. На практике за длительность переходного процесса принимают время, которое прошло от начала процесса до момента, когда выходная величина достигла 95% от ее конечного установившегося значения

Логарифмическая характеристика (л.а.х.):

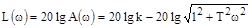                     (2)

При малом значении частоты 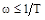 в выражении (2) 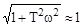, т.е. . Соответственно характеристика будет представлять собой прямую, параллельную оси абсцисс, и проходящую на уровне 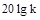. Это есть первая асимптота, к которой стремится л.а.х. при 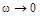. С другой стороны на больших частотах при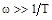 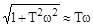, т.е. .

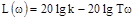В этом случае характеристика представляет собой прямую, имеющую наклон -20 дБ/дек. Действительно, при увеличении частоты в 10 раз, т.е. на декаду

.

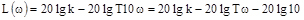Т.о. величина  уменьшилась на 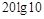, т.е. на 20 дБ.

Эта линия является второй асимптотой, к которой стремится график л.а.х. при 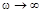. Обе асимптоты пересекаются на частоте: .

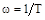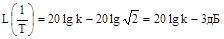
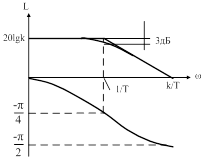
Рис. 29. Логарифмическая частотная характеристика апериодического звена.

Частота 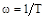 называется сопрягающей частотой.

Таким образом, расхождение между истинной и ассимтотической л.а.х. составляет 3дБ, поэтому при практических построениях л.а.х. апериодических звеньев используют обычно ассимтотические л.а.х.. 

Примером апериодических звеньев первого порядка являются:

1) генератор постоянного тока;

2)  двигатель любого типа (электрический, пневматический и т.д.), механические характеристики которого – прямые линии, для различных входных сигналов;

3) резервуар с газом, жидкостью…;

4)  нагревательная печь;

5)  термопара;

6) электромагнитные, гидро-, пневмоусилители и т.д.