Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.
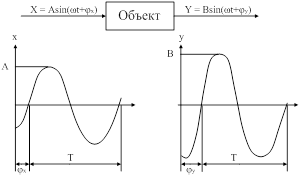
Рис. 24. Экспериментальное определение частотных характеристик объекта.
Пусть на вход звена подано гармоническое воздействие: 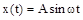 , где
, где 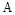 – амплитуда, а
– амплитуда, а 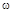 – угловая частота этого воздействия.
– угловая частота этого воздействия.
По окончании переходного процесса на выходе звена будут существовать гармонические колебания с той же частотой, что и входные колебания, но отличающиеся в общем случае по амплитуде и вазе, т.е. в установившемся режиме выходная величина звена будет: 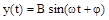 , где
, где 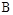 – амплитуда выходных установившихся колебаний,
– амплитуда выходных установившихся колебаний, 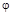 – фазовый сдвиг между входными и выходными колебаниями.
– фазовый сдвиг между входными и выходными колебаниями.
Степень различия между параметрами входных и выходных гармонических сигналов не зависит от амплитуды и фазы входного сигнала, а определяется только динамическими свойствами самого объекта и частотой колебаний.
Поэтому в качестве динамических характеристик объекта могут быть использованы следующие частотные характеристики:
Амплитудно-частотная характеристика (АЧХ) – 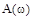 ;
;
Фазо-частотная характеристика (ФЧХ) – 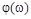 ;
;
Амплитудно-фазовая характеристика (АФХ) – 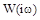 , определяемые по формулам:
, определяемые по формулам:
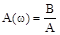 - зависимость отношения амплитуды гармонических колебаний на выходе элемента к амплитуде на его входе от частоты.
- зависимость отношения амплитуды гармонических колебаний на выходе элемента к амплитуде на его входе от частоты.
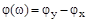 - зависимость изменения фазы выходного гармонического колебания по отношению к фазе входного колебания от частоты.
- зависимость изменения фазы выходного гармонического колебания по отношению к фазе входного колебания от частоты.
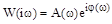 - комплексная функция, для которой АЧХ является модулем, а ФЧХ – аргументом.
- комплексная функция, для которой АЧХ является модулем, а ФЧХ – аргументом.
Частотные характеристики элемента можно определить экспериментально, подавая на его вход синусоидальный сигнал с различной частотой и регистрируя параметры синусоид на выходе (рис. 24). Можно определить частотные характеристики и по другим динамическим характеристикам элемента, в частности, по его передаточной функции.
Как указывалось выше, оператор 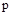 , который является аргументом функции
, который является аргументом функции 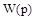 , представляет собой комплексное число и может быть представлен в виде
, представляет собой комплексное число и может быть представлен в виде 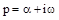 , где
, где 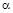 – вещественная часть
– вещественная часть 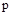 ;
; 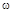 – мнимая часть
– мнимая часть 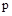 .
.
Оператор 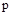 может принимать любые значения, т.е. может быть и чисто мнимой величиной. Возьмем значение
может принимать любые значения, т.е. может быть и чисто мнимой величиной. Возьмем значение 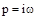 и, подставив его в выражение для передаточной функции
и, подставив его в выражение для передаточной функции 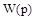 , получим функцию комплексного переменного
, получим функцию комплексного переменного 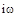 :
: 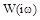 – т.е. АФХ. Как функция комплексного переменного,
– т.е. АФХ. Как функция комплексного переменного, 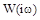 может быть представлена двояко: в полярных координатах
может быть представлена двояко: в полярных координатах 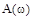 и
и 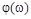 или в прямоугольных координатах
или в прямоугольных координатах 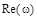 и
и 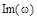 :
:
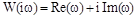 , где
, где 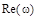 и
и 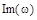 – действительная и мнимая части
– действительная и мнимая части 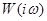 .
.
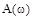 ,
, 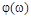 ,
, 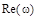 и
и 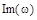 связаны между собой следующими соотношениями:
связаны между собой следующими соотношениями:
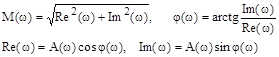
|
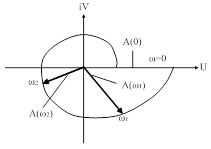
| Рис. 25. Пример построения годографа АФХ. |
АФХ 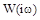 строится в плоскости комплексного переменного и представляет собой годограф вектора, модуль и аргумент которого
строится в плоскости комплексного переменного и представляет собой годограф вектора, модуль и аргумент которого 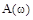 и
и 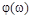 изменяются в зависимости от частоты (рис. 25).
изменяются в зависимости от частоты (рис. 25).
Пример:
Требуется построить частотные характеристики объекта, передаточная функция которого имеет вид: 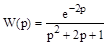
Заменив в 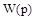
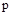 на
на 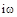 , получим выражение для АФХ:
, получим выражение для АФХ:
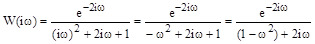
Модуль и аргумент для 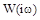 найдем по формулам:
найдем по формулам:
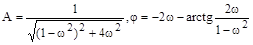
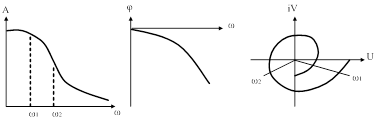
а) б) в)
Рис. 26. Пример построения частотных характеристик а) – АЧХ; б) – ФЧХ; в) – АФХ.
2.8.2. Логарифмические частотные характеристики:
В ТАУ широко используются логарифмические частотные характеристики ЛЧХ: логарифмическая амплитудная ЧХ (ЛАЧХ) 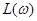 и логарифмическая фазовая ЧХ (ЛФЧХ)
и логарифмическая фазовая ЧХ (ЛФЧХ) 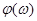 . Они получаются путем логарифмирования передаточной функции:
. Они получаются путем логарифмирования передаточной функции:
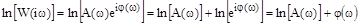
На практике удобнее пользоваться десятичными логарифмами:
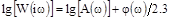
ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования умножается на 20, и используют не натуральный логарифм, а десятичный, т.е. 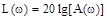 . Величина
. Величина 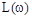 откладывается по оси ординат в децибелах. Изменение уровня сигнала на 10 дБ соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала
откладывается по оси ординат в децибелах. Изменение уровня сигнала на 10 дБ соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала 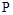 пропорциональна квадрату его амплитуды
пропорциональна квадрату его амплитуды 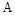 , то изменение сигнала в 10 раз соответствует изменение его уровня на 20 дБ, так как
, то изменение сигнала в 10 раз соответствует изменение его уровня на 20 дБ, так как
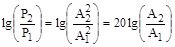
По оси абсцисс откладывается частота ω в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение 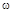 в 10 раз. Такой интервал называется декадой. Так как
в 10 раз. Такой интервал называется декадой. Так как 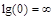 , то ось ординат проводят произвольно.
, то ось ординат проводят произвольно.
ЛФЧХ отличается от ФЧХ только масштабом по оси 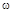 . Величина
. Величина 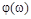 откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы интервала
откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы интервала 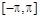 .
.
Дата: 2019-02-19, просмотров: 456.