Составление дифференциальных уравнений основано, как правило, на законах сохранения массы и энергии и уравнениях связи между входными и выходными переменными. Т.е. первым шагом при составлении мат. описания является выявление управляемой переменной и управляющего воздействия, а затем – выявление физического закона, связывающего эти переменные в одно уравнение.

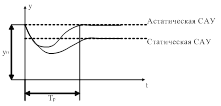
Рис. 16. Графики апериодических переходных процессов.

Рассмотрим САР в установившемся режиме, характеризующемся значением выходной величины 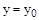. Пусть в момент  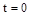на объект воздействовал какой-либо возмущающий фактор, отклонив значение регулируемой величины. Через некоторое время регулятор вернет САР к первоначальному состоянию (с учетом статической точности) (рис. 16). Если регулируемая величина меняется во времени по апериодическому закону, то процесс регулирования называется апериодическим.

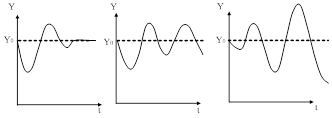
При резких возмущениях возможен колебательный затухающий процесс (рис. 17а). Существует и такая вероятность, что после некоторого времени 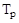 в системе установятся незатухающие колебания регулируемой величины – незатухающий колебательный процесс (рис. 17б). Последний вид – расходящийся колебательный процесс (рис. 17в).

а)                                б)                            в)

Рис. 17. Графики колебательных переходных процессов.

Таким образом, основным режимом работы САУ является динамический режим, характеризующий протеканием в ней переходных процессов. Поэтому основной задачей при разработке САУ является анализ динамических режимов работы САУ.

Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамики 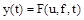, описывающее изменение величин во времени. Как правило, это дифференциальное уравнение, или система дифференциальных уравнений.

Модели систем типа вход – выход описываются дифференциальными уравнениями, которые выражают зависимость (в динамическом процессе) между теми величинами, которые в схеме исследуемой системы указаны на выходе и на входе.

Порядок дифференциальных уравнений может быть очень высоким, то есть зависимостью связаны как сами входные и выходные величины, так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:

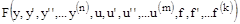
После записи дифференциального уравнения необходимо определить факторы, от которых зависят переменные, входящие в это уравнение.

Дальнейшим шагом является линеаризация полученного уравнения, если линеаризация вообще допустима.