В общем случае уравнение динамики оказывается нелинейным, т.к. реальные звенья САУ обычно нелинейны. В целях упрощения теории нелинейные уравнения обычно заменяют линейными, которые приблизительно описывают динамические процессы в САУ. Получаемая при этом точность уравнений оказывается достаточной для технических задач. Процесс преобразования нелинейных уравнений в линейные называется линеаризацией уравнений динамики. Рассмотрим сначала геометрическое обоснование линеаризации.

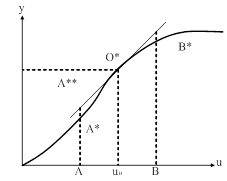
В нормально функционирующей САУ значение регулируемой и других промежуточных величин незначительно отличается от требуемых значений. В пределах малых отклонений все нелинейные зависимости между величинами, входящими в уравнение динамики, могут быть приближенно представлены в виде отрезков прямых линий. Например, нелинейная статическая характеристика звена на участке 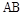 (рис. 18) может быть представлена отрезком касательной в точке номинального режима .

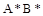Начало координат переносится в точку 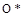, и в уравнениях записываются не абсолютные значения 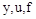, а их отклонения от номинальных значений: 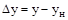, , 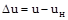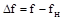. Это позволяет получить нулевые начальные условия, если считать, что при  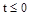система находилась в номинальном режиме в состоянии покоя.

Рис. 18. Линеаризация статической характеристики.

Другими словами, суть линеаризации состоит в замене кривой искомого решения нелинейного уравнения прямой, касательной к этой кривой в точке, соответствующей начальным условиям. Такая замена будет справедлива только для тех отклонений, при которых кривая незначительно отличается от касательной. Следовательно, допустимая область отклонений и определяет возможность линеаризации исходной системы.

Математическое обоснование линеаризации состоит в том, что если известно значение 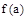 какой-либо функции 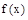, в любой точке 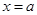, а также значение производных от этой функции в данной точке, то в любой другой достаточно близкой точке  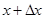значение функции можно определить, разложив ее в окрестности точки в ряд Тейлора: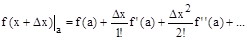

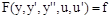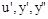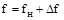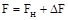Аналогично можно разложить и функцию нескольких переменных. Для простоты возьмем упрощенный, но наиболее характерный вариант динамики САУ: . Здесь производные по времени  также являются переменными. В точке, близкой к номинальному режиму: и . Разложим функцию  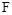в ряд Тейлора в окрестности точки номинального режима, отбрасывая члены ряда высоких порядков малости:

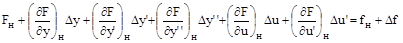
В номинальном режиме, когда все отклонения и их производные по времени равны нулю получаем частное решение уравнения 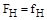. Учитывая это и вводя обозначения, получим:

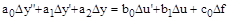
Отбрасывая все знаки ∆, получим:

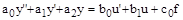
В более общем случае получим

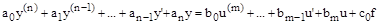При этом всегда нужно помнить, что в данном уравнении используются не абсолютные значения 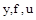, и их производные, а отклонения этих величин от их номинальных значений. Поэтому полученное уравнение будем называть уравнением в отклонениях.

К линеаризованной САУ можно применить принцип суперпозиции: реакция системы на несколько одновременно действующих воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет звено с двумя входам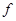и  и 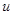 разложить на два звена, каждое из которых имеет один вход и один выход (рис. 19).

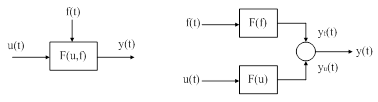
Рис. 19.  Иллюстрация принципа суперпозиции.

Поэтому в дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид:

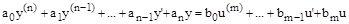
Это уравнение описывает САУ лишь приближенно с той точностью, которую дает линеаризация. Однако следует помнить, что линеаризация возможна только при достаточно малых отклонениях величин и при отсутствии разрывов функции 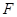 в окрестностях интересующей нас точки, которые могут быть созданы различными выключателями типа реле и т.д.

2.4. Преобразование Лапласа.

В теории автоматического управления широко используется специальный метод прикладного анализа, в основе которого лежит функциональное преобразование Лапласа.

Преобразованной по Лапласу функцией называется комплексного переменного, определяемая соотношением:

,

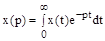где 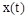 – исходная функция действительной переменной 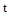, называемая оригиналом,  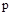– комплексная переменная, 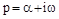,  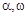– действительные переменные, .

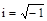Функция 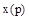 называется изображением по Лапласу функции  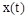и записывается в ви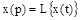де , где 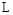 – символ преобразования Лапласа.

Обратный переход от изображения к оригиналу осуществляется по формуле:

,

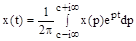где 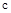 – абсцисса сходимости функции .

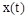Для большого числа функций, встречающихся в практике, составлены таблицы соответствия между оригиналами и изображениями, значительно облегчающими применение преобразования Лапласа.

Широкое использование преобразования Лапласа объясняется рядом преимуществ этого метода перед прямым решением задач в области действительного переменного. В частности, изображения некоторых функций проще, чем их оригиналы.

Пример.

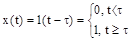
В данном примере оригинал является разрывной функцией времени. Найдем ее изображение:

.

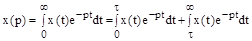Первое слагаемое равно 0, т.к. подынтегральная функция на интервале 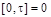. После подстановки во второе слагаемое 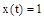, получим

,

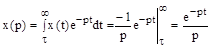т.е. изображение разрывной функции от 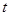 является непрерывной функцией от .

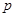Пример.

Найдем изображение для функции .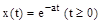

.

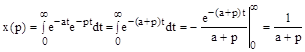Полученное изображение является алгебраической функцией.

Другим важным преимуществом использования преобразования Лапласа является тот факт, что некоторые операции над изображениями проще, чем соответствующие операции над оригиналами.

В результате линеаризации получается линейное дифференциальное уравнение управляемого объекта, которое после преобразования по Лапласу можно представить в виде

,

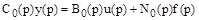где 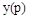– управляемая величина,  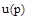– управляющее воздействие,  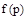– возмущение. Здесь без потери общности учтено только одно воздействие .

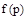Полином 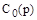 представляет собой характеристический полином управляемого объекта. Он характеризует свободное движение объекта, т.е. его движение пр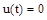и и 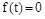под влиянием ненулевых начальных значений 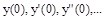, вызванных, например, исчезнувшим к моменту времени  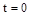возмущающим воздействием 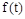. В зависимости от знаков вещественных частей корней этого полинома объект может быть устойчивым или неустойчивым.

Полином 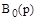 определяет влияние управляющего воздействия  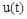на характер изменения управляемой величины.

Полином 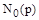 определяет влияние возмущающего воздействия на характер изменения управляемой величины.

Управляющее устройство, как показано на рис. 2, состоит из различных элементов или звеньев. Уравнения некоторых из них известны заранее. Для другой группы элементов дифференциальные уравнения составляются аналогично тому, как это делалось для управляемого объекта.

Совокупность уравнений элементов после преобразования по Лапласу решается относительно выходной величины управляющего устройства 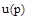. В результате получается дифференциальное уравнение управляющего устройства

,

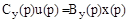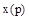 – ошибка системы и до преобразования .

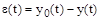Для получения дифференциального уравнения всей системы эти уравнения решаются относительно ее выходной величины, в качестве которой можно рассматривать как управляемую величину 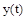, так и ошибку .

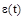В первом случае получается дифференциальное уравнения

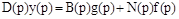,                            (1)

где ; ; .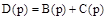

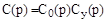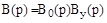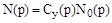Полином 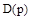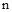-го порядка характеризует свободное движение системы автоматического управления. Он называется характеристическим полиномом замкнутой системы и может быть представлен в виде

,

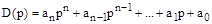где 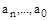 в линеаризованной системе представляют собой постоянные коэффициенты.

Как видно из (1), полином 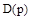 отличается от характеристического полинома объекта 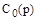. Это означает, что и свободное движение системы может существенно отличаться от свободного движения объекта. В частности, если управляемый объект неустойчив, то при правильно выбранных алгоритме управления и параметрах управляющего устройства система в целом будет устойчивой. Наоборот, при неправильном выборе система автоматического управления устойчивым объектом может стать неустойчивой.

Полином 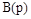 в уравнении (1) определяет влияние задающего воздействия  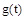на характер изменения управляемой величины 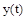, причем последняя должна как можно более точно воспроизводить задающее воздействие, т.е. ошибка системы должна быть минимальной.

Полином 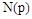 определяет влияние возмущающего воздействия на характер изменения управляемой величины. В уравнении (1) учтено только одно возмущение 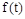. В принципе таких возмущений может быть несколько. Однако вследствие линейности уравнения действует принцип суперпозиции, согласно которому реакция на сумму воздействий равна сумме реакций. Поэтому достаточно рассмотреть методику учета только одного возмущения, а при наличии нескольких возмущений необходимо лишь просуммировать результат.

Во втором случае, когда в качестве выходной величины рассматривается ошибка 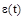, дифференциальное уравнение системы может быть получено подстановкой в (1) выражения для ошибки:

.

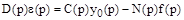Из этого уравнения вытекает, что ошибка системы автоматического управления может быть представлена в виде суммы двух составляющих. Первая составляющая определяется наличием задающего воздействия 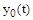, а вторая наличием возмущающего воздействия. Первая составляющая не равна нулю только в программных и следящих системах. В стабилизирующих системах 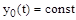. поэтому всегда можно выбрать начало отсчета так, чтобы .

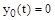Согласно (1) 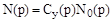, это означает, что выбором структуры и параметров управляющего устройства можно уменьшить вторую составляющую ошибки и тем самым ослабить влияние управляющего воздействия на объект. Если для какого-либо возмущающего воздействия полином 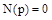, то говорят, что система автоматического управления является инвариантной относительно этого воздействия. Равным образом в программных и следящих системах равенство  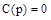означает, что система инвариантна относительно задающего воздействия.