Определение гармонической оптимальности формы осуществляется за счет придания ей трех основных сложных формально-композиционных свойств – целостности, упорядоченности и соразмерности.

Целостность это сложное формально-композиционное свойство формы, характеризующееся наличием соединения, пересечения или наложения контуров визуальных групп композиции.

Большое значение для ощущения целостности архитектурного объекта имеет законченность его структуры. Законченность архитектурной структуры во многом зависит от ее геометрического вида и характера построения деталей, либо ограничивающих форму во всех направлениях, либо дающих возможность продолжения развития композиционного организма.

Законченными формами являются правильные геометрические тела с максимальным количеством одинаковых параметров: шар, куб, тетраэдр и т. д. Античные зодчие считали совершенными фигурами квадрат и круг, как наиболее статичные и законченные.

Законченность архитектурной форме придают и детали. Так, карниз, завершающий здание, композиционно останавливает его развитие вверх.

К общим средствам организации элементов формы в целостную структуру относят также прием использования зрительного тяготения и равновесия масс. Прием использования зрительного тяготения масс – это средство организации элементов в единое целое. Принцип закономерного объединения элементов формы в целое исходит из фактора психологического восприятия тяготения друг к другу близкорасположенных элементов и тяготения «слабых» элементов с малой массой к «сильным» элементам с большой массой, «наивной физики» по Выготскому. При этом срабатывает принцип «пятна», заключающийся в том, что отдельные элементы воспринимаются как силуэты, стремящиеся слиться в единое изображение; как объемы, соединяющиеся друг с другом.

Равновесие масс также является средством достижения целостности формы. Если элементы формы уже объединены согласно принципу тяготения масс, можно стремиться использовать более тонкое средство организации – сложную закономерность равновесия масс элементов относительно точки или оси равновесия. При этом совокупности визуальных масс элементов должны быть уравнены относительно них.

Принцип равновесия масс особо важен в асимметричных композициях.

Симметрия – это такой случай равновесия масс, при котором относительно центра, оси или плоскости симметрии располагаются равные не только по массе, но и по геометрическому виду элементы.

Симметрия как средство организации автоматически обеспечивает всей системе равновесие относительно центра или оси симметрии и определенную целостность, но не всегда создает композиционное единство. Для его обеспечения необходимо чтобы в центре или на оси симметрии размещался главный как по форме, так и по содержанию элемент композиции.

Симметрия играет огромную роль в организации элементов в целостную структуру. Бинокулярность зрения, симметричность построения человеческого тела сказываются на наших представлениях не только о равновесии, но и гармонической упорядоченности симметричной формы. Симметрия может рассматриваться и как категория порядка, способствующая объединению архитектурных форм. В сложной форме композиционные средства тесно связаны друг с другом и только условно, в целях анализа их можно искусственно расчленить[20].

Упорядоченность это еще одно формально-композиционное сложное свойство формы, характеризующееся размещением композиционных центров второстепенных элементов на динамических осях главных по отношению к ним элементов, размещением участков и динамических осей элементов по ясному для наблюдателя закону.

Организация архитектурных форм в гармоническую структуру подразумевает определенную закономерность в их сочетании – композиционную систему их объединения в единое целое. К аспектам этой проблемы относятся: принципы расстановки объемов в пространстве, характер объединения частей в единое целое, способ членения формы и некоторые другие закономерности.

Одним из наиболее общих подходов к упорядочению формы являются ряды, которые можно рассматривать и как средство организации элементов в единую устойчивую систему на основании закономерного упорядоченного чередования элементов формы.

Ряд – это система элементов, основанная на периодичности повторения или изменения однозначных свойств формы.

Периодическая закономерность – это такая закономерность, при которой отношение между первым и вторым элементом такое же, как

между n и ( n + 1) – элементами.

Период ряда – это его элемент, который закономерно повторяется или изменяется. Период включает в себя как форму, так и интервал (пространство), отделяющий ее от других форм в окружающей среде. Периодом ряда может быть одна форма и интервал или совокупность форм и интервалов. Как форма, так и среда могут быть и телом и пространством. Ряд как средство организации особо важен при необходимости объединения в единое целое большого числа элементов (более 7±2) – верхнего предела числа Миллера, характеризующего объем кратковременной памяти человека.

В целостной и устойчивой, точки зрения восприятия, системе элементов роль каждого элемента ослаблена из-за их большого числа, но характер каждого элемента еще воспринимается. Однако, при этом, закономерность, организующая эти элементы в единое целое, прочитывается ясно и отчетливо. Общее число элементов ряда обычно больше, но меньше числа, при котором они, соотнесенные с целым, начинают восприниматься как элементы фактуры.

Метрический ряд организуется в соответствии с тождеством периодов по всем объективным свойствам формы.

Ритмический ряд строится согласно принципа подобия периодов, нюансном или контрастном неравенстве и закономерном изменении периодов по одному, нескольким, либо по всем объективным признакам формы. Периоды, при этом, изменяются от модификации только форм, только среды или форм и среды одновременно. Изменение нескольких объективных признаков формы может проходить параллельно – нарастая или убывая в одном направлении или встречно – когда в одном направлении нарастает один признак, а в противоположном направлении – другой. В первом случае динамичность формы выражена ярче, во втором она нивелируется. Ряды могут быть простыми и сложными, одной или двух закономерностей. В сложном ряду двух закономерностей одна из них доминирует, определяя основную закономерность, организующую единство элементов в целом. Всегда доминирует закономерность, определяющая отношение периодов ряда.

Основой сочетания элементов в единое целое – порядка – является определение главного элемента композиции и соподчинение всех остальных по степени значимости. Принцип иерархии, таким образом, является главным и определяющим в достижении гармонично упорядоченной формы.

Использование принципа единообразия в расчленении формы и ее элементов также способствует достижению упорядоченности. Яркое свидетельство этого – греческие классические ордера («ordo» - порядок).

Закономерности организации элементов, их упорядочение лежат и в основе цветовой гармонии. Упорядоченные элементы цветовой композиции могут образовывать качественно новую систему – цветовую гармонию. Структура цветовой гармонии основана на тех же закономерностях, что и объединение элементов пластической композиции. Элементы цветовой гармонии своими различиями по цветовому тону обеспечивают цветовое богатство, разнообразие палитры – гаммы. В зависимости от того, нюансно или контрастно различаются основные цветовые элементы гармонических палитр, гаммы этих палитр соответственно нюансны или контрастны.

Соразмерность – это сложный комплекс оптимальных соотношений формы с окружающей средой, человеком, а также частей формы друг с другом и целого с частью. Главную роль как основные средства гармонизации формы в решении этой задачи играют архитектурный масштаб и пропорциональные закономерности.

Архитектурный масштаб представляет собой эстетическую характеристику величины архитектурного содержания, ее соответствие значению объекта, среде и человеку. Таким образом, архитектурный масштаб является одним из важных средств эстетической выразительности. В понятие архитектурного масштаба входит как количественная сопоставимость архитектурных форм и среды, так и качественная, связанная с идейно-художественным значением объекта и его общественной функцией. На формально-композиционном уровне архитектурный масштаб определяет степень крупности членений формы по отношению к форме в целом или степень крупности интервалов между формами. При этом, чем меньше расчленена форма, тем крупнее масштаб и наоборот.

Масштабность формы является субъективной эстетической оценкой степени соответствия формы и ее частей размерам человеческого тела напрямую и опосредованно, через размеры окон, дверей, ступеней. Свойство восприятия человека определять величину всех объектов в сравнении с установившимися эталонами широко используется в архитектуре и искусстве.

Оптические иллюзии всегда присутствуют при восприятии соразмерности формы через ее расчлененность, цвет, свет и другие признаки. В силу этого, они могут использоваться для корректировки формы в аспекте придания ей задуманной масштабности.

Мощным средством достижения соразмерности и оценки ее наличия являются пропорции и пропорциональный строй формы. Пропорционирование тесно связано с подобием форм и их элементов.

Понятие пропорции в античности было аналогично понятию соответствие, сходство, подобие. Сходные формы облегчают задачу приведения различных пространственных элементов к единству. Подобие может быть полным и неполным (например, квазисимметричным, дисимметричным или аффинным – с общим типом структуры, но с разной конфигурацией, например, аксонометрия является аффинной проекцией). Полное или геометрическое подобие нескольких форм характеризуется общностью их структуры (пространственного построения) и общей пропорциональной взаимосвязью габаритов. Известный способ построения подобных прямоугольников за счет параллельности или перпендикулярности их диагоналей не обязательно приводит к гармонической взаимосвязи между ними. Для их сведения в пропорциональную систему, определяющую пропорциональный строй и обладающую внутренней закономерностью, их габариты следует уменьшать или увеличивать по определенному закону. Например, если у подобных прямоугольников длина одного равна высоте другого, то образуется так называемая непрерывная пропорция a:b=b:c, так как b=d. Величина b является средним пропорциональным для a и с. Габариты подобных форм могут уменьшаться или увеличиваться как с помощью числовых зависимостей, так и геометрическим построением.

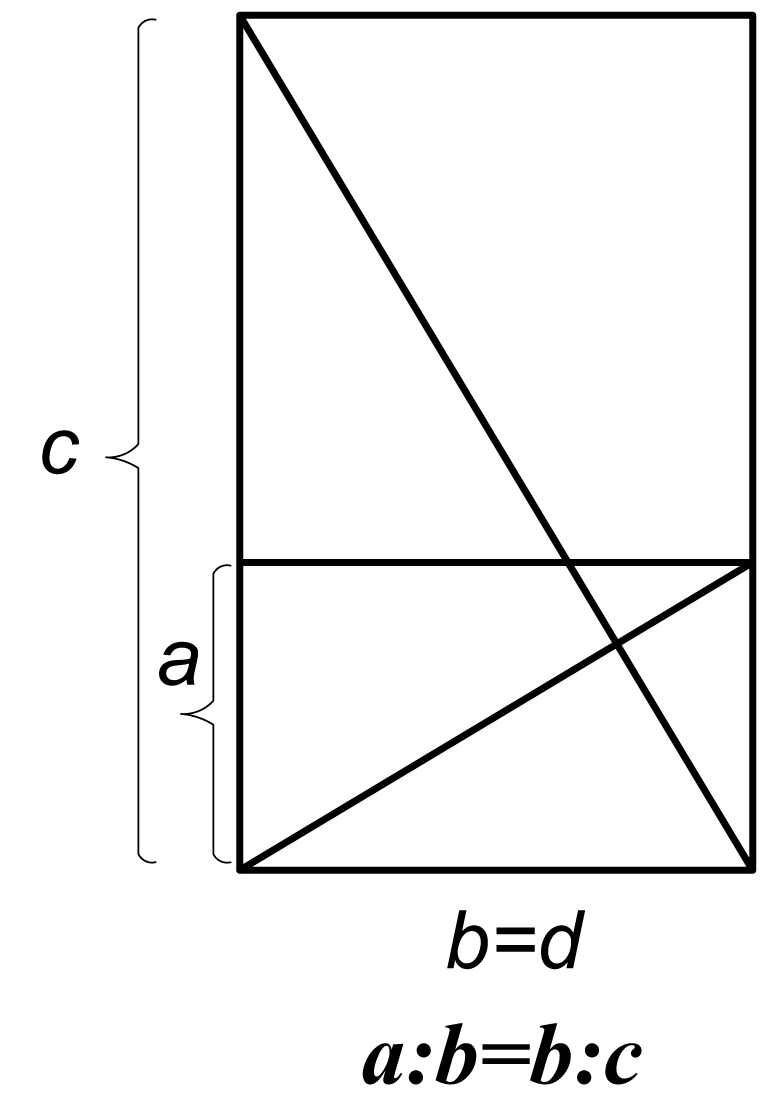
Рис. 57. Принцип построения непрерывной пропорции.

Изменение габаритов исходного прямоугольника за счет прибавления постоянной величины образует арифметическую прогрессию. При умножении величин сторон на постоянное число получается геометрическая прогрессия. В архитектуре более широко используется аддитивный ряд (сложения), когда каждый последующий член ряда равен сумме двух предыдущих, такие ряды также известны, как возвратные, определяемые рекуррентными формулами (в т.ч. ряд Фибоначи). Ряд, в котором каждый последующий член равен квадрату предыдущего является видом геометрической возратной прогрессии (первый член задается произвольно). Взаимосвязь между членами ряда может быть как рациональной, так и иррациональной.

Рассмотренные выше сложные формально-композиционные свойства формы выступают как критерии оптимальности и одновременно как средства ее гармонической организации.