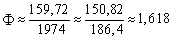Из древнейших шумерских городов известны Эриду, Урук, Ур, Лагаш, Ларса, Умма, Ниппур, Кута и другие. Все они имели план овального очертания, ориентировались на северо-запад и юго-восток, в центре города располагался священный участок, на котором на холме или искусственной террасе располагалось святилище прямоугольной формы и высокая башня-зиккурат. Парадоксально, но принципам пропорционально- геометрического построения зиккураты предположительно связаны с домонгольским культовым зодчеством Руси.
Материалы исследований ряда теоретиков древнерусского зодчества (работы П. Н. Максимова, А. А. Тица, К. Н. Афанасьева, Ю. С. Ушакова, Б.А. Рыбакова, И. Ш. Шевелева и др.) и существующие косвенные свидетельства использования древними зодчими архитектурного опыта своих предшественников, воздействия архитектуры Византии, впитавшей, в свою очередь геометрическую и строительную культуру более древних цивилизаций и приграничных стран, позволяет сделать некоторые существенные предположения о методах геометрического построения архитектурной формы русскими мастерами раннехристианского (домонгольского) периода.
1. При возведении раннехристианских храмов на Руси был первичен объемно-пространственный, «идеальный» замысел формы как суммы объемных элементов разного геометрического вида: параллелепипеда, цилиндра, полуцилиндра, призмы, пирамиды, сложных поверхностей вращения. Фактические подтверждения тому: прикидочные наброски и разбивочные схемы – рисунки на стенах подвала Успенской церкви в Александровой слободе г. Рязани (см. рис.13) и на стене придела Иоанна Богослова в Новгородском Софийском соборе в Тамани (Тмутаракани). Также имеются нефактические, на уровне предания, сведения о возможном изготовлении и объемных моделей для проверки замысла будущего сооружения.
2. Архитектурная форма как сумма элементов разного геометрического вида, структурно-композиционное построение уже на стадии «идеального» замысла этих элементов носило глубокий семантический внутрихристианский смысл.
3. Конкретизация идеально-абстрагированной схемы формы и определение конкретных закономерностей ее построения на местности определялась степенью развития прикладной геометрии и осуществлялась в последовательности: ПЛАН - ФАСАДЫ (РАЗРЕЗЫ) - ОБЪЕМ.
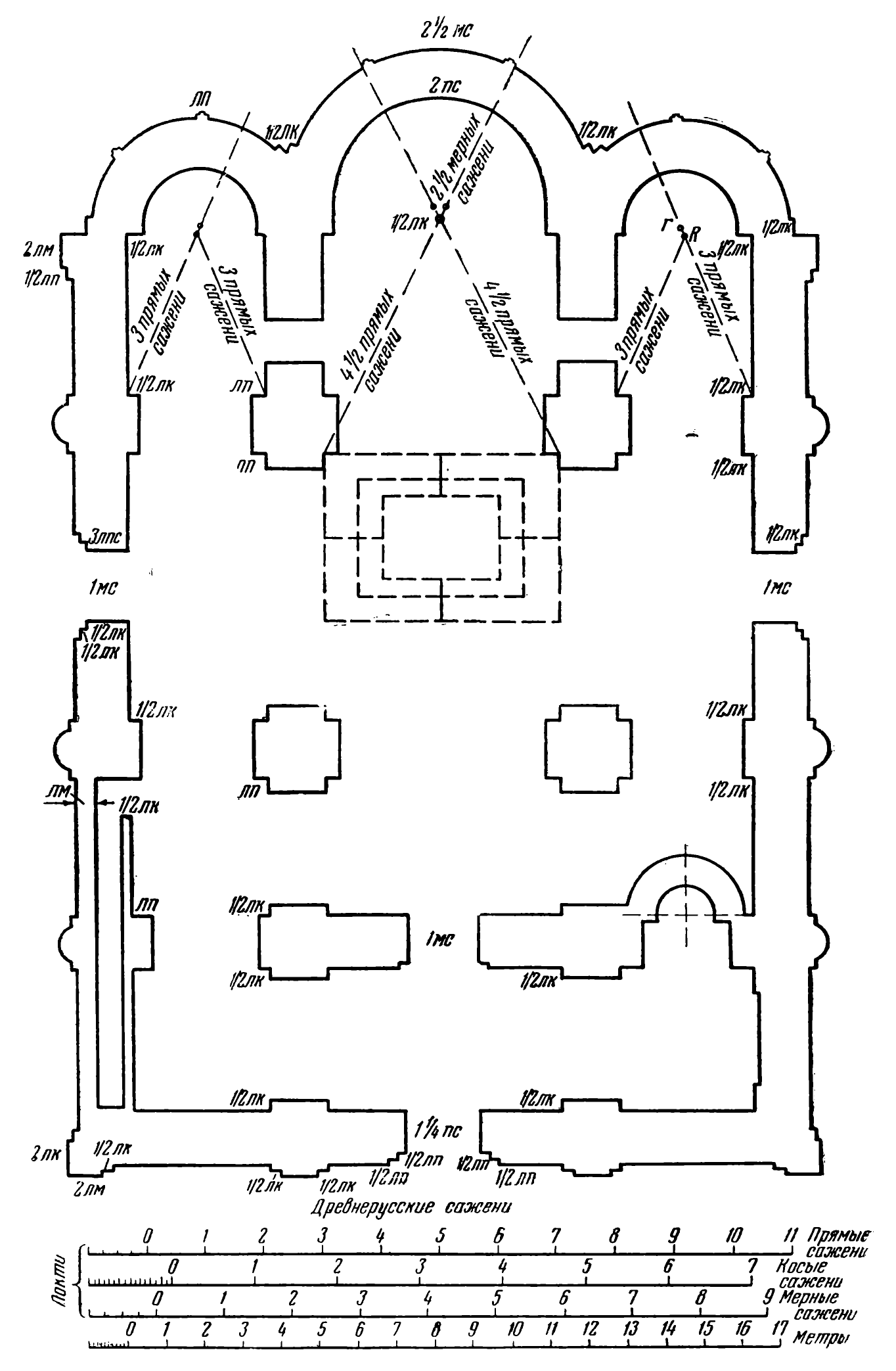
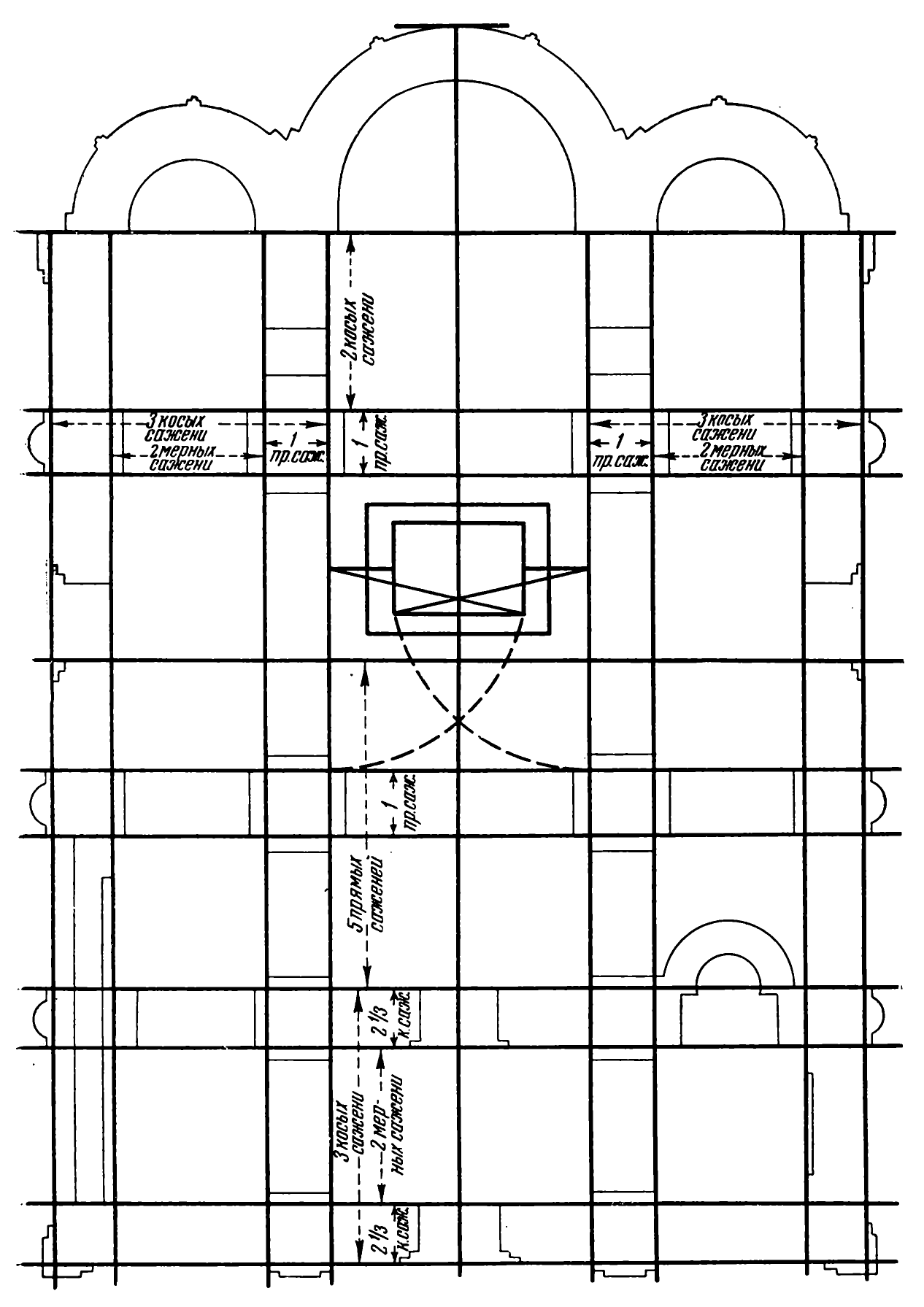
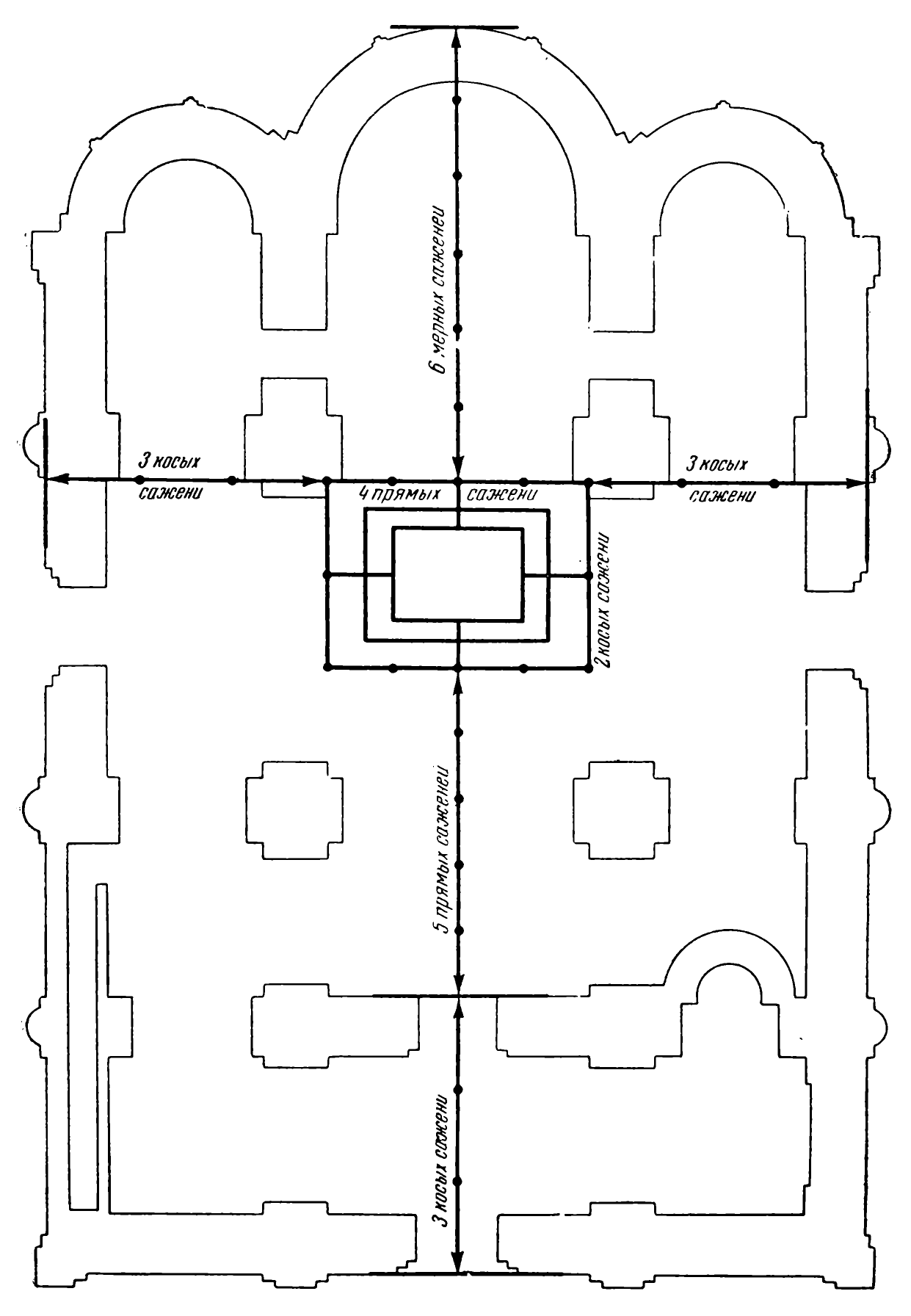
В основе организации целой архитектурной формы лежал план сооружения, взаимосвязь частей которого определялась геометрическим построением по принципу – «от общего к частному» и «от частного к общему» (см. рис. 8, 9). Использовался модульный принцип построения и прием геометрического подобия общего и частного, когда за основу брался плоскостной размерно-геометрический модуль (ПРГМ) – квадрат или прямоугольник. «Размер центрального купола или подкупольного квадрата неизменно являлся тем начальным звеном цепи построения соразмерностей, которое можно назвать модулем всего построения – модулем, понятым не как единица, служащая для кратного сопоставления со всеми размерами сооружения, а как исходный размер в цепи геометрических соответствий». Так считает К.Н.Афанасьев – исследователь пропорциональных построений культовых объектов домонгольского периода. Квадрат как геометрическая фигура, элементарно строящаяся и обладающая рядом замечательных свойств, обеспечивающих возможность построения геометрических сопряженностей и соразмерностей частей плана, фасада и разреза, служил опорным звеном «вавилонов» древнерусских зодчих. Прием пропорционирования сооружений на основе «вавилона», т.е. сетки вписанных друг в друга квадратов и прямоугольников и их диагоналей, позволял создавать структурно-композиционные построения на основе динамической симметрии: симметрии подобия, предвосхитившей открытие фрактальной симметрии Б. Мальдебротом в XX в.
Математическое содержание таких схем, по мнению Б.А. Рыбакова, имеет родство с геометрическим принципом пропорционирования зиккуратов. Современные находки шумерских глиняных табличек II тысячелетия до н.э. с аналогичными построениями на территории Ирака (г. Ниппура) подтверждают эти гипотезы. Таким образом, один и тот же пропорционально-динамический принцип построения формы лег в основу совершенно разных архитипов структурно-композиционного построения формы: зиккурата и крестовокупольного храма домонгольской Руси.
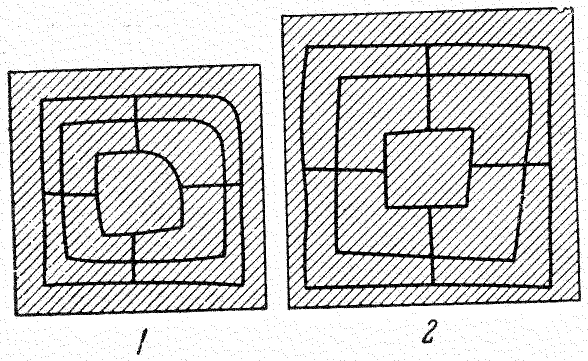
Рис. 8. Кирпич IX в. со знаком «вавилона» (Саркел)


Рис.9. Шумерские (г. Ниппур) таблички, возможно являются т.н. «вавилонами» для пропорционирования длин: доказательства существования практической и теоретической математики (II тыс. до Р.Х.) до Пифагора и Евклида.
Рис.10. Графическое изображение русских саженей и их долей по принципу «вавилона» (по Б. А. Рыбакову, 1949)
Математические ряды вписанных один в другой по принципу самоподобия и соразмерности квадратов – 1, Ö2, 2, 2Ö2, 4,…; и целочисленных прямоугольников - Ö1, Ö2, Ö3, Ö4, Ö5,…, Ön, Ön+1 получались при помощи геометрических построений (см. Рис). Такие построения позволяли мастерам средневекового храмового зодчества выбирать в качестве основы строения плана и объема разные геометрические сопряженности на основе системы саженей. Последовательность соразмерностей в строении плана, фасадов и деталей выражалась в условно-графических схемах – «вавилонах», сохранившихся на кирпичах, черепице и представляющих собой врисованные друг в друга квадраты или прямоугольники. На основе выбранного сочетания мер, по мысли Б.А. Рыбакова, давалось задание «плинфотворителям». Предположительно, «вавилоны» можно трактовать, как формализованные схемы Ноева ковчега – то есть геометризацию идейного замысла храма.
Рис.11. Реконструкция французского чертежа XII в., изображавшего Ноев ковчег (по В. П. Зубову)
В центре чертежа изображается два вписанных квадрата; внутренний делят на четыре малых квадрата. Затем продолжают стороны этого квадрата (названного в тексте «локтем») в четырех направлениях для получения длины и ширины ковчега. К сожалению, изложение процесса вычерчивания написано неким Гуго очень сбивчиво и неясно, да и сам мифический объект изображения не способствовал внесению ясности. Предположительно, автор хотел в своем сочинении передать читателям технику пользования квадратным «вавилоном», но так как на Западе она была неизвестна, то он и не смог по-настоящему об этом рассказать. Осталось неясным, для какой цели внутренний квадрат («локоть») делится на четыре части. Для чего понадобилось продолжать стороны «локтя» в четырех направлениях, тогда как в тексте говорится лишь о двух. Вероятно, сам автор плохо знал ту зодческую мудрость, которую собирался пересказать другим. Может быть, после крестового похода появились какие-то сведения о восточных архитектурных приемах, основанных на системе вписанных квадратов, но сочинение Гуго полностью их не раскрывает. Труд «О таинственном значении ноева ковчега» важен для нас указанием на то, что чертежник прежде всего чертил в центре будущего сооружения систему квадратов, пересеченных линиями, близкую к изучаемым нами «вавилонам».
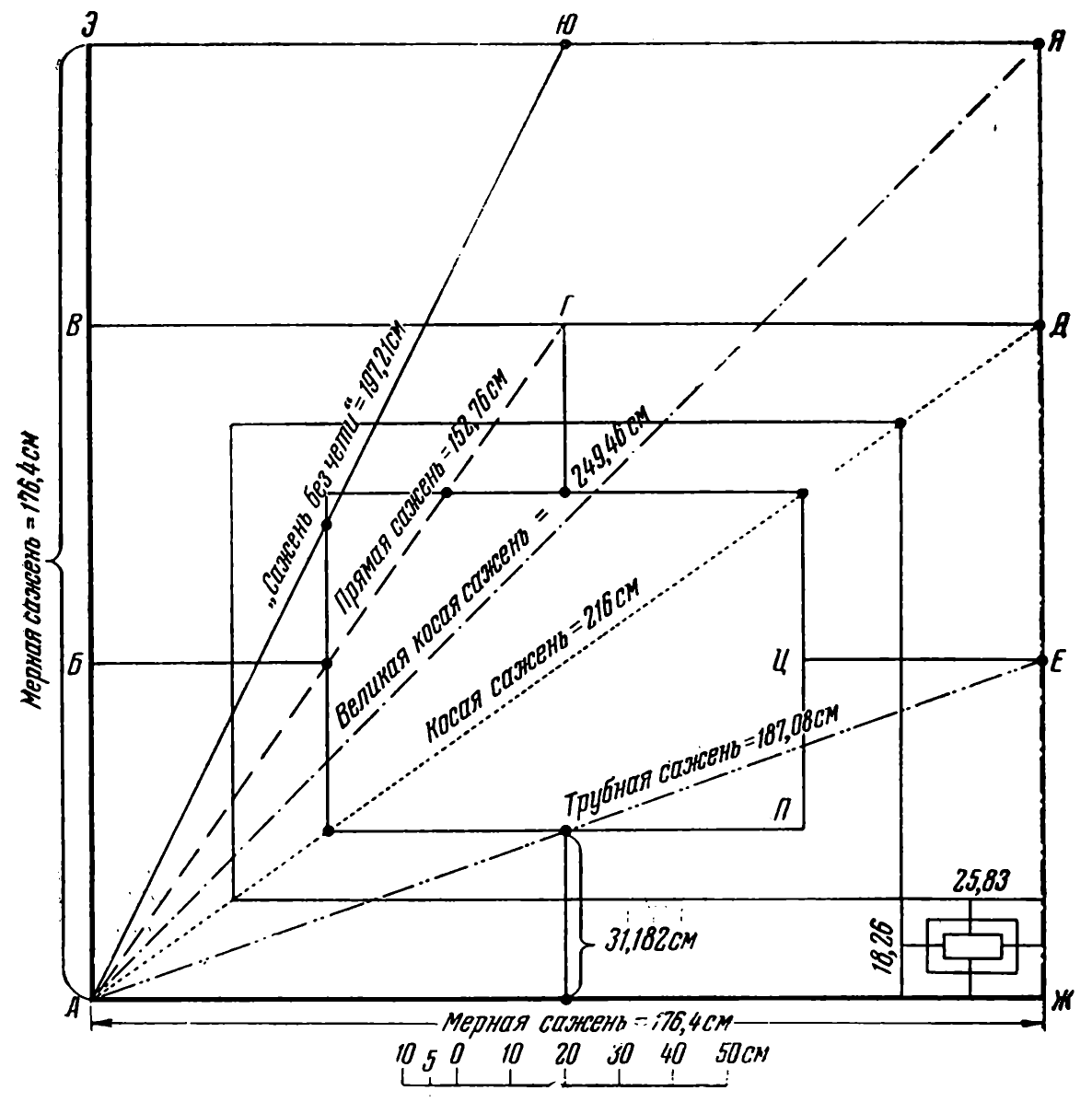
Рис. 12. Расчетный чертеж XII в. Старая Рязань. а — «вавилон»; б — отобранные из него линии.
Анализ рязанского чертежа (Рис.) убеждает в том, что здесь перед нами отобранные для каких-то целей линии геометрических сопряженностей «вавилона» (рис. ).
|
| 
| |
| Рис. 13. Успенская церковь Елецкого монастыря. Рязань. | |||
| А.Предполагаемая последовательность плана -«очертания» Успенской Елецкой церкви: определение общих габаритов | Б.Предполагаемая последовательность разбивки плана -«очертания» Успенской Елецкой церкви. Построение опорных столбов стен, нефов и нартекса (притвора в ширину храма) | В.План-реконструкция Успенской Елецкой церкви | |
|
|
| ||
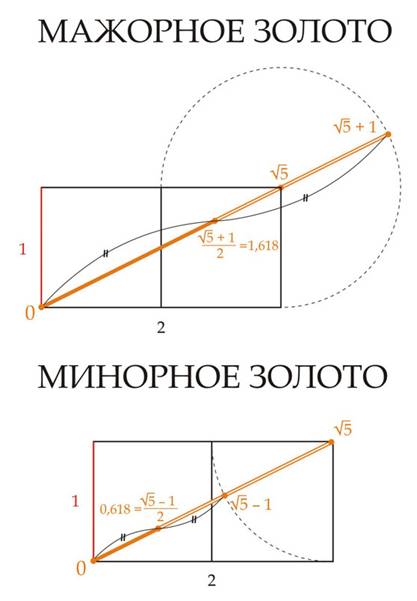
| Рис.14а. Построение «минорного» и «мажорного» вариантов «золотой» пропорции. (по рис. Н. Введенской).
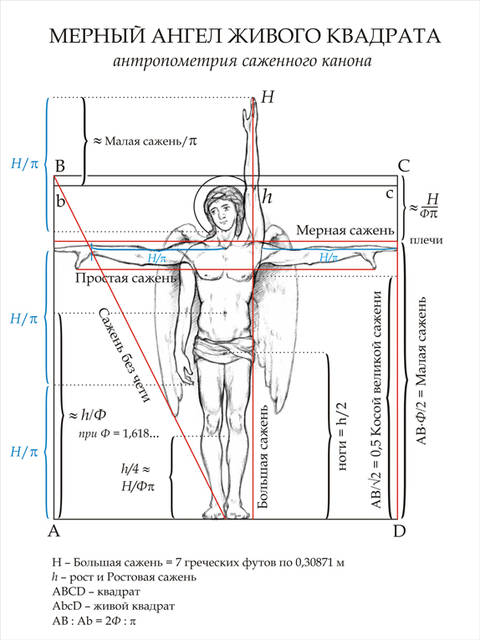
| Рис.14б. Мерный «ангел». Построение «минорного» и «мажорного» вариантов «золотой» пропорции в саженной системе, антропоморфизм (по рис. Н. Введенской). | ||
Взаимосвязь древнерусских мер длины, по утверждению И.Ш. Шевелева, позволяла заранее представлять себе не только абсолютные размеры будущей постройки, но и ее пропорциональный строй, не прибегая к составлению чертежей в масштабе. Саженные меры длины и система их сопряженностей выросла на основе некоторых последовательных заимствований. Применение греческого фута при строительстве в ХI веке первых древнерусских храмов показано К. Н. Афанасьевым. Использовалась и т. н. «филетерийская оргия»), по разным источникам варьируется от 2,14 до 2,16 м (древнерусская сажень большая), и греческая оргия в 2,3 м. К ХII в. система вновь эволюционировала и семь греческих футов стали так называемой большой саженью (2,161 м). Отзвук этого события до сих пор живет в русской поговорке «семь раз отмерь, один раз отрежь». Византийские математики, создавая крестово-купольный храм, использовали систему антропоморфных пропорций, разработанную еще в античности, в которой работают и золотое сечение, и число π, выраженное как т. н. «подходящая дробь» 22/7. При этом использовались меры, удобные для строителей, сопоставимые со средними размерами человеческого тела. В этом кроется причина того, что мерные ряды античной, византийской и русской домонгольской архитектуры сопрягаются с пропорциями человеческого тела. Отношение 103: 100 (размах рук к росту) - можно выразить как удвоенное «золото», деленное на π, то есть отношение мерной сажени к ростовой. Еще в античной Греции, а затем в Византии была известна замена иррациональных величин «подходящими дробями» или целыми мерами по принципу геометрических сопряженностей «вавилона», на Руси [великая сажень] = √2 х [сажень маховая], т.е. великая сажень равна диагонали квадрата со стороной, равной маховой сажени. Число π и оказалось материализованным в антропоморфных пропорциях (также, как и Ф, и √2), диаметр двойного мажорного золота (√5 + 1) : π = 1,03007...
Схема строения плоскостной формы фасадов в значительной степени повторяла схему формы плана (очертания апсид в плане соответствуют очертаниям закомар на фасаде). Об этом свидетельствуют совмещенные изображения древнейших произведений древнерусского книжного искусства – «Остромирове евангелие (1056 – 57)», «Изборник Святослава (1073)».
Прием совмещения плана с фасадом или разрезом определяет основные соотношения между шириной, длиной и высотой здания. Последняя определялась при этом шириной или длиной. Схема формы «пятого фасада» - венчающей части общей формы здания во многом зависела от очертаний боковых фасадов и представляла собой совокупность криволинейных поверхностей, ограничивающих и завершающих объем.
Форма здания, полученная как производная от идеальной схемы, но имеющая конкретные параметры – формальные характеристики, фиксировалась в виде графических схем и служила основой материальной формы при разметке основания сооружения на местности, корректировки его размерно-пространственной структуры, уточнения мерности членений деталей и основного объема.
В средневековом русском зодчестве проблема геометрического построения формы предстает как трехэтапная задача. Две первые ее составляющие имеют характер выбора идеальной символической схемы, а последняя составляющая касается практического воплощения. Таким образом, даже в столь далекие времена созданию материальной формы предшествовала в той или иной степени детализированная ее геометрическая модель формы (далее по тексту ГМФ), что подтверждают пропорциональные соответствия между изображениями храмов в летописных источниках и оригиналами храмов на Руси.
На протяжении многих веков архитектурное формообразование и композиция базировались на манипуляциях со сложившимися типами композиций структур сооружений и их элементов - морфотипами. Устойчивость и узнаваемость архитипов (морфотипов) архитектурной формы (далее АФ) позволяет даже говорить о своеобразной типологии форм памятников архитектуры и возможности создания обобщенных моделей их структурно-композиционного построения.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
| | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
От древнерусских саженей до наших дней
Установим связь между знаменитой пропорцией и множеством разнообразных древнерусских саженей.
В древнерусской числовой системе архитектурного пропорционирования, которая применялась задолго до монгольского нашествия, в качестве единиц измерения использовался некоторый набор инструментов под общим названием “сажени”. Причем саженей было несколько, разной длинны и, что особенно необычно, они были несоразмерны друг другу и использовались при замере объектов одновременно. Историки и архитекторы затрудняются установить их количество, но признают наличие не менее семи типоразмеров саженей, которые имеют собственные названия, определяемые, по-видимому, характером предпочтительного применения.
О том. когда зародилась эта, на первый взгляд “нелепая”, по мнению архитекторов и археологов, “собранная с миру по нитке” древнерусская система измерительные инструментов, неясно. Различные авторы по-разному определяют время её возникновения. Так, А. Ф. Черняев, инженер, академик Международной Академии
информации в своей работе ссылается на следующие точки зрения.
Вторая точка зрения была отражена в работах историка с мировым именем Б. А. Рыбакова. Он полагал, что большая часть мер появилась у славян в период XII—XIII вв., развивалась и совершенствовалась примерно до XVII в. Но Б. А. Рыбаков также не исключал возможность привнесения в древнерусскую систему измерительных инструментов каких-либо элементов из других сопредельных и отдаленных стран. Таким образом, указанные два отрезка времени разделяют почти полтора тысячелетия.
К точке зрения Б. А. Рыбакова близка точка зрения известного историка математики и педагога И. Я. Депмана. Он говорит следующее:
«Первое упоминание о сажени, равной трем локтям, имеется в летописи под 1017 г. Маховой саженью называлось расстояние между концами пальцев распростертых рук. косой саженью — расстояние от каблука левой ноги до конца пальцев подмятой вверх правой руки (давалось и другое объяснение происхождения длины косой сажени). В: отличие от маховой и косой сажени, приравненная в XVI в. к трем аршинам сажень называлась новой, царской, казённой, печатной или орлённой».
В разных книгах название древнерусской меры “сажень” производится от английского слова fathom. Однако нет никакой надобности искать корень слова “сажень” в иностранных языках. По “Толковому словарю живого великорусского языка” Владимира Даля слово “сажень” имело в старое время форму “сяжень”. Глагол “сягать”, в настоящее время не употребляемый, сохранился в языке в форме “досягать”, в словах “досягаемый”, “недосягаемый”. Глагол “сягать” означал доставать до чего-либо,
откуда выражения: “разум сягает, да воля не владеет”, “рука не сягает” и т.д. отсюда естественное объяснение слова “сажень” или “сяжень”: досягаемое (рукой при косой сажени) расстояние.
Чем же было вызвано появление множества саженей? Современному человеку кажется нелепым существование нескольких эталонов измерения для проведения одной и той же операции. Почти два столетия ученые пытаются восстановить секреты возникновения «невзаимосвязанных» измерительных инструментов и привести это множество к минимальному количеству типоразмеров, опираясь на определенные исходные предпосылки, чаще всего связанные с пропорциями человеческого тела или с пропорциями геометрических фигур, например квадрата.
Б. А. Рыбаков выделял две наиболее распространенные системы измерения: новгородско-псковскую и московско-владимиро-черниговскую. Автор констатировал одновременное существование в Древней Руси с X по XVII в. только семи видов саженей (некоторые сажени и их части показаны на рис.) и не отмечал в системе саженей такой единицы, как вершок. Приведем таблицу выделенных им длин саженей, в которую дополнительно включим вершок.
Б. А. Рыбаков отметил следующие особенности применения саженей. • Возможность измерения одного и того же объекта разными видами саженей. Одновременное применение разных мер длины объясняется строгими геометрическими соотношениями, заложенными в них. • Графическое построение по двум системам мер длины (по простой и мерной саженям) древних схем — «вавилонов» (системы вписанных квадратов), возможное предназначение которых – установление пропорций и соотношений используемых саженей. Изучая свойства «вавилонов», историк отметил следующие закономерности, определяющие соотношения между саженями (здесь за а = 88.2 см принята половина маховой сажени).
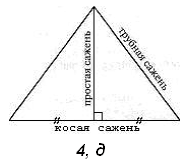
Зависимость Проанализировав работу архитектора А. А. Пилецкого, который исследовал системы пропорционирования в древнерусской архитектуре, А. Ф. Черняев приводит набор двенадцати древних саженей, полученный метолом усреднения многих образцов измерительных инструментов. Сажень городовая – 284,8 см; Сажень без названия – 258,4 см; Сажень великая – 244 см; Сажень греческая – 230,4 см; Сажень казённая – 217,6 см; Сажень царская – 197,4 см; Сажень церковная – 186,4 см; Сажень народная – 176 см; Сажень кладочная – 159,7 см; Сажень простая – 150,8 см; Сажень малая – 142,4 см; Сажень без названия – 134,5 см; А. Ф. Черняев отметил следующую закономерность. Найдем последовательные отношения величин пяти самых больших саженей к пяти самым маленьким:
Число 1,618… обозначают буквой Ф, Ф =
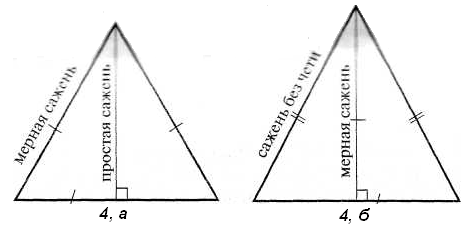
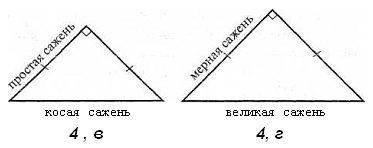
По мнению А. Ф. Черняева, от исследователей ускользнула самая простая и самая совершенная из возможных систем пропорционирования, изначально заложенная в структуру древнерусских саженей, - пропорционирование по золотому сечению. Иначе говоря, кратность всех саженей числу Ф! Возможная причина этого заключается в том, что заранее предполагали: церковная сажень имеет в основе древнеримские пассы, греческая – греческие оргии, Великая сажень – шведский медвежий локоть, царская – египетский царский локоть и т.д. Автор заключает, что соразмерность и эстетическая привлекательность памятников древнерусского зодчества являются следствием особой подвижной функции взаимосвязанного комплекса древнерусских саженей, заключающейся в том, что их основное назначение – соизмерение. Сажени – инструмент соизмерения и пропорционирования. А. Ф. Черняев подчеркивает, что сажени “не статические линейки, а остановленные длинною продолжающиеся динамические процессы”. Именно по этому архитектурные памятники Древней Руси своей соразмерностью и пропорциональностью превосходят типовые “коробки” XIX и XX вв. – детищ очень точного стандартного метра. Как свидетельствуют археологические находки, “метод вавилонов” применялся древними мастерами для пропорционирования саженей по некоторым эталонам без знания дробей и умения извлекать квадратные корни. А. Ф. Черняев не исключает, что мастера использовали способы восстановления размеров по любой сохранившейся сажени (и даже при отсутствии эталона - по любому прутку с размером, близким к пропорции человека), например с помощью построения треугольников. Автор предполагает следующий способ восстановления эталонной сажени. Возьмем деревянный пруток длиной, равной росту плотника, например 172 см, что почти соответствует мерной (маховой) сажени. Примем этот пруток за базисную длину. Если из трех таких прутков сложить равносторонний треугольник, его высота будет равна 148,96 см, что близко по длине простой сажени (рис. 4. а). Если к середине мерной сажени под прямым углом приставить другую мерную сажень и соединить их свободные концы длинными прутками, то получим равнобедренный треугольник с боковыми сторонами, равными 197,22 см, - аналог сажени без чети (рис. 4, б). Возьмем две полученные простые сажени, соединим их концы под прямым утлом. В полученном прямоугольном равнобедренном треугольнике гипотенуза равна 216,04 см - аналог косой сажени (рис. 4, в), В прямоугольном равнобедренном треугольнике с катетами, равными мерной сажени, гипотенуза равна 243,24 см - великой сажени (рис. 4, г). Наконец, трубную сажень можно получить, если к середине косой сажени под прямым углом приставить простую сажень. При соединении их свободных концов получим равнобедренный треугольник с боковой стороной 187,08 см - аналогом трубной сажени (рис. 4, д).
Восстановление основных саженей окончено. Не восстановлена только морская сажень. Но А. Ф. Черняев отмечает, что и Б. А. Рыбаков сомневался в существовании морских саженей как самостоятельной меры. «Сопряженность русских мер была основой гармоничных решений в архитектурных сооружениях. Создав систему саженей, основанную на пропорциях человеческого тела, русские зодчие получили мощный инструмент для тонкого архитектурного варьирования, передачи в пропорциях целой гаммы оттенков». Вышесказанное еще раз подтверждает тезис: золотое сечение — один из основных принципов представления человека о красивом. Золотая пропорция и различные виды симметрии - причина эстетической привлекательности предметов искусства, объектов живой и неживой природы. Современная наука выявила связь золотого сечения с симметрией. Так, русский кристаллограф Т. Б. Вульф полагал, что золотое сечение есть одно из проявлений симметрии. Закономерности такой «золотой симметрии» проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов, в строении отдельных органов человека и тела в целом. Золотая пропорция играет важную роль в современном дизайне, в частности в автодизайне. Основатель отечественного художественного конструирования (стайлинга) автомобилей, видный отечественный дизайнер Ю. А. Долматовский (1913-1999); в своих работах особое внимание уделял пропорционированию частей кузова автомобиля, настаивая на применении именно пропорций золотого сечения или производных от него. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Лекция 2.
Дата: 2019-02-19, просмотров: 739.

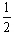 полсажени
полсажени
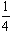 локоть
локоть
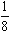 пядь
пядь
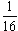 пясть
пясть
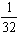 вершок
вершок




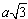 = 88,2 · 1,732 = 152,76
= 88,2 · 1,732 = 152,76
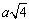 =88,2 · 2 = 176,4
=88,2 · 2 = 176,4
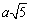 = 88,2 · 2,236 = 197,21
= 88,2 · 2,236 = 197,21
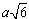 =88,2 · 2,45 = 216,04
=88,2 · 2,45 = 216,04
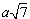 =88,2 · 2,646 = 233,4
=88,2 · 2,646 = 233,4
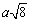 =88,2 · 2,828 = 249,46
=88,2 · 2,828 = 249,46
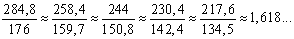
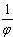 . Таким образом, длины указанных видов саженей находятся в золотом отношении! Для доказательства пропорциональности числу Ф оставшихся царской и церковной саженей достаточно удвоить длину кладочной и простой саженей и разделить полученные результаты на длину царской и церковной саженей соответственно:
. Таким образом, длины указанных видов саженей находятся в золотом отношении! Для доказательства пропорциональности числу Ф оставшихся царской и церковной саженей достаточно удвоить длину кладочной и простой саженей и разделить полученные результаты на длину царской и церковной саженей соответственно: