Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ОСНОВЫ ТЕОРИИ АРХИТЕКТУРНОГО ФОРМООБРАЗОВАНИЯ

 

Учебно-методическое пособие

по подготовке к лекциям

 

 

для студентов ННГАСУ, обучающихся по дисциплине

 «Основы теории архитектурного формообразования»

по направлению подготовки 07.03.01 Архитектура,

профиль: Архитектурное проектирование

 

 

Нижний Новгород

ННГАСУ

2016

УДК 72. 011

 

Голов Г.М. Основы теории архитектурного формообразования: учебно-метод. пос. /Голов Г.М., Чеберева О.Н.; Нижегор. гос. архитектур.- строит. ун-т – Н.Новгород: ННГАСУ, 2016. - –157 с.– 1 электрон. опт. диск (CD-R).

 

 Учебно-методическое пособие для подготовки к лекциям построено в соответствии с авторской методикой Геннадия Михайловича Голова (1948-2015) с акцентом на формальном структурно-композиционном морфогенезе на основе формально-композиционной комбинаторики первоэлементов: точки, линии, контура, поверхности (плоскости), объема. Содержание процесса структурно-композиционного построения архитектурной формы раскрыто, как художественно-композиционная деятельность архитектора в соединении с математическими подходами к моделированию пространственных структур. Рассмотрены стратегии зрительного восприятия архитектурной формы, иерархия формально-композиционных простых и сложных признаков формы, основополагающие формально-композиционные свойства формы – первичные (простые) и вторичные (сложные комплексные), смоделированы алгоритмы неоптимизированного и оптимизированного формообразования. Определяется понятие геометрической модели формы (ГМФ), геометрического элемента (ГЭ) формы, вводится аналитический интеллектуальный инструмент формальной структурно-композиционной комбинаторики ГЭ формы (матрица - морфер). На основе аналогий природоподобия введены методы синтезации и трансформации, определяющие основную массу способов и приемов комбинаторно-геометрического построения формы. Раскрыты формально-композиционные и геометрические основы моделирования архитектурной формы, особенностей ее анализа и синтеза. Освещена типология и вопросы организации точечных, линейных, поверхностных (поверхностно-линейных, топологических) и объемных структур.

 

Предназначено для обучающихся в ННГАСУ по дисциплине «Основы теории архитектурного формообразования», направлению подготовки 07.03.01 Архитектура,

Профиль: Архитектурное проектирование

Учебно-методическое пособие ориентировано на обучение в соответствии с календарным учебным графиком и учебным планом ННГАСУ по основной профессиональной образовательной программе направления 07.03.01 Архитектура, профиль: Архитектурное проектирование

 

 

© ННГАСУ, 2016

©Г. М. Голов, О.Н. Чеберева, 2016

 

 

СОДЕРЖАНИЕ:

 

I.	Раздел 1: Архитектурно-исторический	5
	Лекция 1. 1.1 Введение. Исторический аспект художественно-композиционных закономерностей в архитектуре и других видах искусства. 1.2.   Проблема формы в древнерусском зодчестве.	5
	Лекция 2.  2.1. Структура архитектурной формы и её формально-композиционные свойства: 2.2. Базовые положения процесса неоптимизированного формообразования.	19
	Лекция 3. 3.1.Оптимизированное формообразование и его композиционные характеристики    3.2. Формально-композиционные первичные признаки формы.	32
	Лекция 4. 4.1. Формально-композиционные вторичные признаки формы. 4.2.Простые формально-композиционные свойства формы (средства гармонической оптимизации).	54
	Лекция 5. 5.1. Сложные формально-композиционные свойства формы (критерии гармонической оптимальности). 5.2. Формально-композиционный анализ признаков и свойств формы.	64
II	Раздел 2. Теоретический.	74
	Лекция 6. 6.1. Базовые принципы формально-композиционного формообразования.         6.2.Приемы формально-композиционной синтезации (интеграции) формообразующих элементов.	74
	Лекция 7. 7.1. Приемы формально-композиционной трансформации формообразующих элементов. 7.2. Геометрические закономерности формально-композиционного формообразования	83
	Лекция 8. 8.1. Особенности построения точечных формально-композиционных структур. 8.2. Особенности построения линейных формально-композиционных структур.	114
	Лекция 9. 9.1. Особенности построения поверхностных формально-композиционных структур. 9.2. Особенности построения объемных формально-композиционных структур.	133
	Библиография	155

                                                                                       

 

Раздел I. Архитектурно-исторический.

 

Эти правила, язык знаков и грамматика Игры, представляют собой некую разновидность высокоразвитого тайного языка, в котором участвуют самые разные науки и искусства, но прежде всего математика и музыка (или музыковедение), и который способен выразить и соотнести содержание и выводы чуть ли не всех наук. Игра в бисер – это, таким образом, игра со всем содержанием и всеми ценностями нашей культуры, она играет ими примерно так, как во времена расцвета искусств живописец играл красками своей палитры. Всем опытом, всеми высокими мыслями и произведениями искусства, рожденными человечеством в его творческие эпохи, всем, что последующие периоды ученого созерцания свели к понятиям и сделали интеллектуальным достоянием, всей этой огромной массой духовных ценностей умелец Игры играет как органист на органе, и совершенство этого органа трудно себе представить – его клавиши и педали охватывают весь духовный космос, его регистры почти бесчисленны, теоретически игрой на этом инструменте можно воспроизвести все духовное содержание мира.

Лауреат нобелевской премии

Г. Гессе, « Игра в бисер»

 

Лекция 2.

Таблица 1.

Исследователь	Уровень осуществления комбинаторных операций со знаками, символами	Уровень осуществления комбинаторных операций с формальными геометрическими структурами
Г. Фехнер	Ассоциативный фактор	Формальный фактор
С. Пронин	Концептуальный уровень	Формальный уровень
Глазычев, Капустин, Нечаев	Визуальный язык архитектуры: бытовой диалект	Профессиональный метаязык
Д. Л. Мелодинский	Знаковая плоскость	Объектная плоскость
Ч. Дженкс, Р. Вентури	означаемое	означающее

 

Предметно-пространственное окружение человека подразделяется на естественную и искусственную среду со своими формами и присущими им характеристиками по содержанию. Искусственная среда создается человеком для обеспечения его жизнедеятельности и состоит из предметно-пространственного окружения, из явлений, процессов, идей, организационных структур и пр. Возникающие в чем-либо потребности определяют содержание и форму различных необходимых объектов искусственной среды. Содержание предопределяет компоненты структуры объекта и, следовательно, форму в целом. Оно является, в определенной мере, идеальной составляющей будущего элемента среды, материализующейся через определенную форму. Следует заметить при этом, что определенность формы не однозначна, соответствие конкретной формы конкретному содержанию поливариантно: известному содержанию может отвечать определенное множество форм, содержание полиморфно. Выбор конкретной формы зависит от замысла, идеи архитектора, деятельность по организации новых форм называется формообразованием.

Архитектурная форма в рассмотрении теории архитектурного формообразования представляет собой профессионально-архитектурную абстракцию или угол рассмотрения реальности, где всякое целое рассматривается как принадлежность архитектуры и существует за счет такого взаимодействия своих «частей», которое определяется законами гармонии и выразительности, с одной стороны, целесообразности – с другой.

Дуализм архитектурной формы-массы в том, что «Форма лишь организует пространство, которое и является функционально наполненным элементом архитектурно-художественной, композиционной среды.

Согласно И.Г. Лежаве, «пространство противостоит архитектурной форме, а с другой стороны, организуется ею», поэтому архитектурная форма может быть представлена как форма – масса, как форма – пространство и как смешенная массо-пространственная форма.

В архитектурной практике имеются объекты, обладающие только формой-массой: обелиски, триумфальные арки, монументы и пр., а также массо-пространственные объекты. Последние объекты преобладают, а пространство может быть внутренним и внешним (интерьерным и экстерьерным). Интерьерные пространства характерны для архитектурных моно-объектов, а экстерьерные пространства присущи градостроительным образованиям. Пространственные формы приобретают свои геометрические параметры за счет ограничивающих их форм-масс.

Масса и пространство в геометрии архитектурной формы находятся в отношении антисимметрии.

Специфика архитектурной формы заключается в том, что она с одной стороны является средством и средой для обеспечения материальной составляющей жизнедеятельности человека, а с другой стороны обращена к духовному, эстетическому началу в его жизни, участвуя в создании психофизиологического комфорта среды обитания.

Архитектурное формообразование является базовым процессом архитектурно-проектной деятельности и может быть условно подразделено на три основных подпроцесса: функциональное формообразование (социальная определенность формы); композиционное формообразование (эстетическая определенность формы) и конструктивное формообразование (материально-техническая определенность формы).

В реальном проектировании подпроцессы интегрируются в единый процесс архитектурного формообразования (АФ) влияют один на другой. Поэтому в мире существуют «рядовые», стандартные по форме объекты архитектуры и штучные «произведения». Архитектор, создавая форму объекта, не может одновременно заниматься творческими поисками в рамках всех подпроцессов АФ, а выделяет какой-то ведущий процесс. При этом он обязательно учитывает «пограничные» условия смежных подпроцессов. На практике это выражается в учете комплекса требований, предъявляемых к основному в данный момент деятельности подпроцессу, а также соотнесению и сопоставлению их с требованиями двух других.

Изучение особенностей архитектурного формообразования целесообразно проводить без учета смежных подпроцессов, используя принцип абстрактно-формального моделирования, соединяющего знания теории формальной композиции и геометрии, изучающей метрическое пространство, пространственные отношения и формы тел.

Системный подход в исследовании позволяет детально проанализировать архитектурную форму в пределах одного подпроцесса, выявить ее основные объективные признаки, свойства, а через них законы и закономерности приемы и способы формообразования.

В традиционной архитектуре основой обучения композиции были элементы стиля и их сочетания, с начала XX века – геометрия и формальные геометрические основания композиции, со второй половины XX века – философские концепции как основа поисков формально-геометрических закономерностей построения формы.

 Важнейшим комплексным свойством архитектурной формы является ее идейная, образная, семантическая, знаковая насыщенность, как совокупность визуальных характеристик, отражающих в изобразительном или беспредметном ключе общественное мировоззрение, подчеркивающих определенные социальные и культурные ценности. Важность данного свойства свидетельствует о преобладающей роли структурно- композиционного формообразования в процессе архитектурного формообразования и определяет его как процесс проектирования идеологического характера формы. Правильность данного положения подтверждается также особенностями зрительного восприятия человека, заключающимися в приоритете фиксации композиционных параметров формы архитектурных объектов.

Объекты предметно-пространственного мира обладают рядом основополагающих свойств, рассмотрение которых необходимо для анализа процесса структурно-композиционного формообразования. В материальном мире форме, как структуре, соответствует определенное содержание в виде сущности – внутренней основы, содержания, смысла, сути, как самого главного и существенного, что и определяет ее внутреннее строение, устройство и содержание. В философском смысле форма определяется как способ существования и способ выражения содержания. Символ (от греч. «симболон») некая узнаваемая или упрощенная, схематизированная часть отсутствующего целого, способная напомнить о нем. Форма любого объекта предметно-материального мира может быть аппроксимирована (заменена с упрощением) структурой-композицией  геометрических тел различной мерности (ГТРМ) для проведения полноценного изучения их признаков, свойств и качеств. Это аналитическое расчленение и обратный синтез – основа современной архитектурной комбинаторики.

Геометрическая модель формы (ГМФ) является аналогом формы объекта материального мира в идеально-абстрагированном виде и носителем его содержания. Геометричность – объективное структурно-композиционное формоопределяющее свойство объектов реального мира, в котором проявляется закон единства и борьбы противоположностей. Он выражается в соответствии и обратимости ГМФ и оригинала, их симметрии подобия, хотя степень этой симметрии может быть разной, возможна квазисимметрия, квазиподобие.

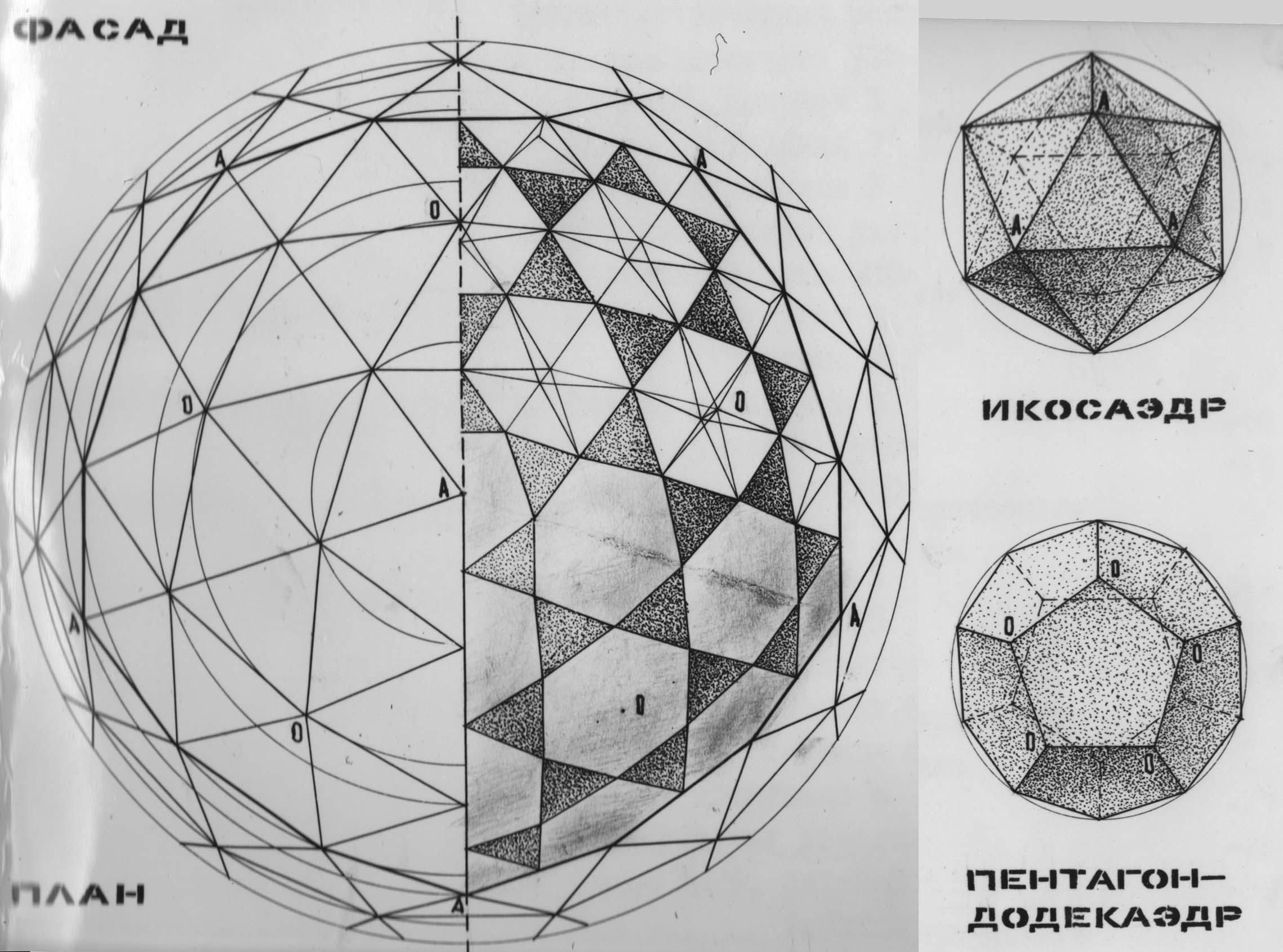
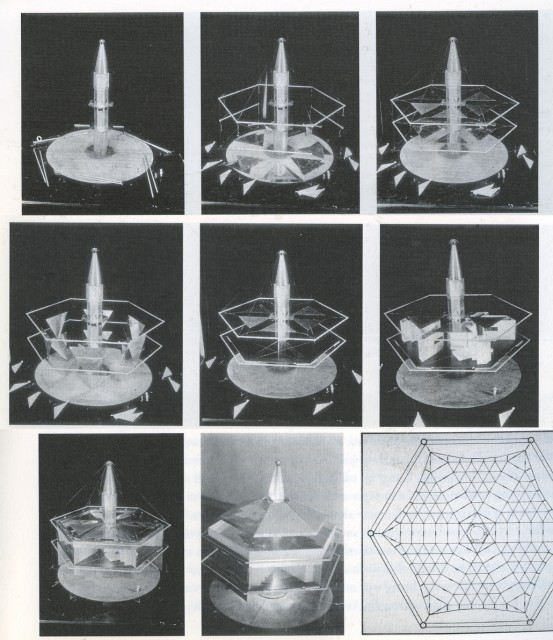
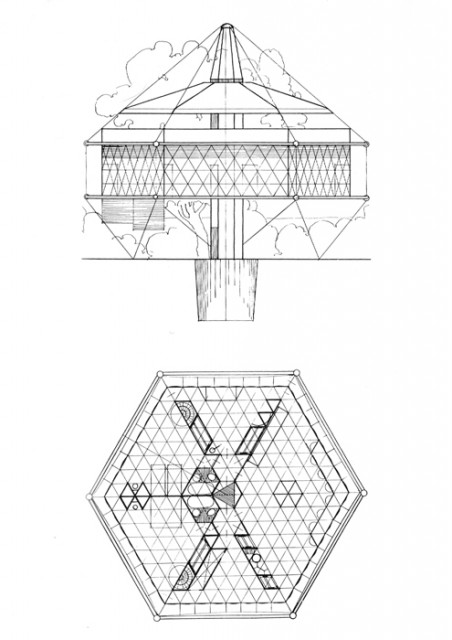
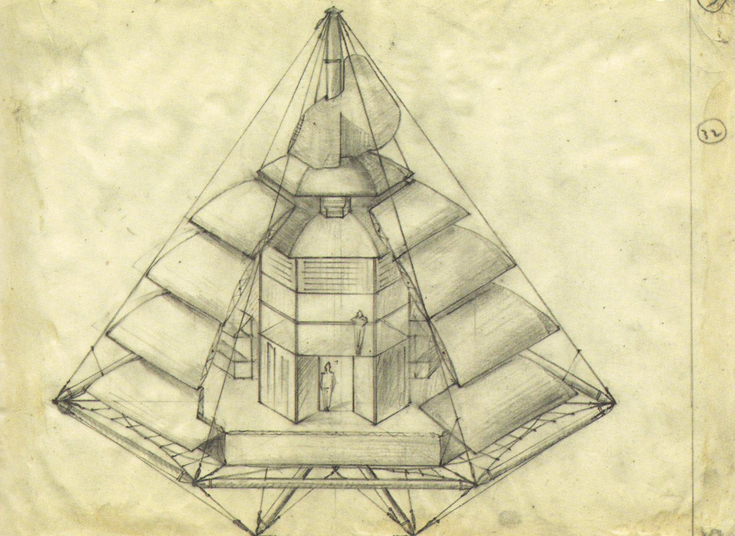
Чертежи генпланов фасадов, планов, разрезов являются простейшими проекционными ГМФ в архитектуре, исторически они могли иметь разную степень точности (см. рис). Изготовление каменных и глиняных геометрических моделей (макетов) наиболее сложных фрагментов храмов в эпоху античности подтверждено археологическими данными, как и т.н. «парадигм» - деревянных моделей ордера (ствол колонны, база, капитель и фрагмент антаблемента) для доставки на место строительства в качестве образца каменотесам и резчикам.

Рис.15. Старинный чертеж - приближенная геометрическая модель формы. Вершина Спасской горы в Павлове, Нижегородской области. Чертеж 1797 г.
РГИА. Ф. 1088. Оп. 10. Д. 533. Дело о постройке в селе Павлове каменной церкви взамен деревянной; переписка графа Н.П. Шереметева с епископом Нижегородским о состоянии церковных сумм и о постройке в вотчине каменной церкви, 1797-1803.

Современное компьютерное моделирование геометрических параметров формы позволяет получить ГМФ высокой степени точности, но идейное семантическое наполнение ГМФ моделируется сознанием проектировщика. ГМФ может быть представлена как одно геометрическое тело (ГТ) или как совокупность геометрических тел различной мерности (далее ∑ГТРМ)* – точек, линий, поверхностей и объемов в любых сочетаниях. Любая ГМФ, следовательно, может быть фиксирована как состоящая из отдельных геометрических элементов (ГЭ), являющихся в каждом конкретном случае ее исходными, первичными элементами. Если ГМФ обозначена в виде ГТРМ, то она также раскладывается на составляющие ее компоненты.  Все ГМФ имеют явно или неявно выраженную полиэлементность. Так даже в точке, как абсолютно малой ГМФ, выделяются при ее графическом изображении такие компоненты как:

- линейный контур, той или иной конфигурации;

- срединная зона, в виде плоского пятна (двухмерное изображение) или    тела с очертанием той или иной сложности.

В линейной ГМФ вычленяются ее начало, конец и середина. В поверхностной ГМФ можно увидеть линейный контур и срединную часть. В объемной ГМФ имеется множество составляющих: поверхности и их границы, линии пересечения поверхностей, линии ребер, точки пересечения ребер. ГМФ с явно выраженной полиэлементностью характеризуются дискретным (прерывистым, скачкообразным) изменением границ, а с неявно выраженной полиэлементностью – синкретным (непрерывным) изменением. Представителями последних являются: точка, прямая линия, линия постоянной кривизны и шар – единственная из трехмерных форм. Согласно вышеизложенному полиэлементность является достаточно широким понятием и выступает как объективное композиционное и формообразующее свойство объектов реального мира и выражает закон меры. Этот закон проявляется в количественно-качественных отношениях элементов, объединяемых в ГМФ через соответствие меры элемента мере всей формы. Дифференцированность ГМФ, проявляющаяся в полиэлементности, предопределяет сущность организации элементов формы в целое – сложную интеграцию или элементарное объединение, группировку, простую сумму компонент формы. Любая форма в геометрическом аспекте является синтезом n-го количества взаимосвязанных определенным образом ГЭ. Среди приемов объединения можно выделить следующие: блокировка, наложение, вложение, охватывание, группировка.

Совместное использование данных приемов характеризует способы образования новых форм. Объединение элементов ГМФ может быть контактным, бесконтактным и комбинированным.

Композиции масс по степени мерности подразделяют на фронтальные (двухмерные) и объемные (трехмерные). В случае преобладания пространства над массой или существенной роли пространства в композиции ее определяют как глубинно-пространственную. Однако, и в объемной, и в глубинно-пространственной композиции характерно организующее ее начало – наличие определенной геометрии форм-масс, организованных композиционно при помощи их геометрического построения. Контактное объединение характерно для организации форм-масс из компонент также в виде форм-масс. Здесь определяющим фактором (архетипом мышления зодчего) является масса и ее геометрия как антитеза пространству, которое осваивает зодчий и которое является основным функциональным наполнением архитектурной формы.

Бесконтактное объединение предполагает интеграцию исходных элементов, представляющих собой формы-массы и формы-пространства. При этом, элементы первого типа взаимодействуют между собой через составляющие 2-го типа, что характерно для градостроительных объектов.

*Σ Сумма. Л.Эйлер (1755).

Сумма – результат сложения величин (чисел, функций, векторов, матриц и т. д.). Для обозначения суммы n чисел a1, a2, ..., an применяется греческая буква "сигма" Σ: a1 + a2 + ... + an = Σni=1 ai = Σn1 ai. Знак Σ для суммы ввёл Леонард Эйлер в 1755 году.

Комбинированное объединение является ведущим и наиболее применяемым. Оно заключается в совместном использовании контактного и бесконтактного объединения, что используется при создании отдельных объектов и объектно-пространственных систем.

Таким образом, полиэлементность, как формообразующее свойство позволяет выделить интегрируемость (Возможно, термин образован от латинского integer – целый)  в качестве основы метода синтезации ** новых форм.

** от Synthèse

По-гречески слово synthesis означает союз, состав, соединение. Синтезировать означает составлять (tithenai) вместе (sun). Тем самым синтез противостоит анализу, то есть расчленению, разложению. Современная теор ия композиции, в основном, подвергает имеющиеся произведения архитектуры и градостроительства анализу. Формообразование, как творческий процесс, противостоит анализу, но является его закономерным продолжением. Синтез идет от простого к сложному по Лейбницу. По части имеющихся элементов он составляет (или восстанавливает) целое. Анализ идет от сложного к простому. Он разделяет целое на элементы. Примером тому могут служить химические процессы. Соединяя атомы кислорода и водорода, можно синтезировать воду. И наоборот, подвергнув ее анализу, можно получить атомы кислорода и водорода. Однако в философии слово «синтез» используется в основном для обозначения умственного процесса, состоящего только из идей. Именно так понимает синтез Декарт. Синтез является третьим, после очевидности и анализа, правилом его метода: «Располагать свои мысли в определенном порядке, начиная с предметов простейших и легко познаваемых, и восходить мало-помалу, как по ступеням, до познания наиболее сложных» («Рассуждение о методе», часть II). Из этого следует, что анализ – первый (простое не дано изначально; его еще надо завоевать) и ближайший из истинных путей, благодаря которым была методически изобретена каждая вещь (см. «Возражения…»). Синтез в основном служит доказательству того, что уже известно. Достаточно сравнить, например, «Размышления о первой философии» того же Декарта, написанные в аналитическом ключе, и его же «Первоначала философии», выстроенные по принципу синтеза. Но синтез – не только порядок или метод. У Гегеля и Маркса это также один из аспектов диалектики. Две противоположности соединяются, образуя третий, превосходящий термин (то есть уничтожающий и одновременно сохраняющий обе), – это и есть синтез. Таково становление как синтез бытия и ничто (Гегель. «Наука логики», раздел I, глава 1). Таков плод как синтез семени и растения (Энгельс. «Анти-Дюринг», отдел I, глава 13).

Анализ ГМФ на различных этапах существования их оригиналов указывает на изменяемость характеристик формы во времени в зависимости от различных факторов и условий. Эта изменяемость носит всеобщий характер и выступает как трансформируемость формы, - еще одно объективное композиционное формообразующее свойство объектов реального мира, в котором выражается закон развития. Трансформируемость проявляется в модификации ГФ, ГМФ через изменение габаритов и мерности формы, позволяя тем самым организацию новых форм по методу трансформации. Для данного метода характерны следующие приемы создания новых форм: отсечение, расчленение, изгиб, скручивание, растяжение, смятие, складывание и др. Прием в данном случае понимается как аналог физического воздействия, предшествующего определенному качественному изменению формы.

Трасформация может быть по аналогии с полиморфизмом в неживой природе динамическим качеством формы объекта, осуществляющимся за счет перестроения ее элементов (полиморфизм кристаллов — в физике, минералогии, химии существование кристаллических веществ с одинаковым составом, но разной структурой).

Тема 2.2. Базовые положения процесса неоптимизированного формообразования.

 

Прямое использование методов синтезации и трансформации позволяет получать новые ГМФ, имеющие случайный характер и не обладающие, эстетическими композиционными характеристиками. Это происходит в силу определенной «механистичности» процесса образования форм без ориентации на получение определенного конкретного результата и без комплекса требований, предъявляемых к нему и создаваемым формам. Процесс организации формы, при этом, определяется как неоптимизированное формообразование. Он абстрактен и формы, получаемые на его основе, следует рассматривать как схематичные. При рассмотрении, они определяют только геометрический вид формы (ГВФ) и представляют собой простую совокупность ГТРМ. Доминирующий здесь принцип случайности во многом оправдывает получение таких результатов, как иррациональность форм, свидетельствующая об отсутствии разумного, логического начала. Эффект отключения мышления при организации данных форм свидетельствует об определенной «природности» неоптимизированного формообразования, его физиомиметической сущности, т.к. его начала лежат в закономерностях живой и неживой природы, и свойствах человеческого сознания к невольному бессознательному и волевому копированию, отображению и модификациям этих природных методов формообразования. В природном окружении можно найти множество примеров проявления процесса неоптимизированного формообразования. Осенние листья, падающие с деревьев, выстилают на земле своеобразный мозаичный ковер и свидетельствуют о существовании приема наложения в рамках метода синтезации. Сосульки, свисающие с обреза крыш зданий, с веток деревьев во время оттепели, также подтверждают природность данного формообразования и являются проявлением метода трансформации, в частности, приема гравитационного формования. Природное, иррациональное формообразование является источником всех знаний о построении новых форм, так как предоставляет весь необходимый материал для исследования.

Данный метод изучения возможностей архитектурного формообразования имеет сущностные отличия от бионики Лебедева, биомиметики, т.к. исследует весь спектр процессов формообразования, встречающихся в природе (см. рис. 16).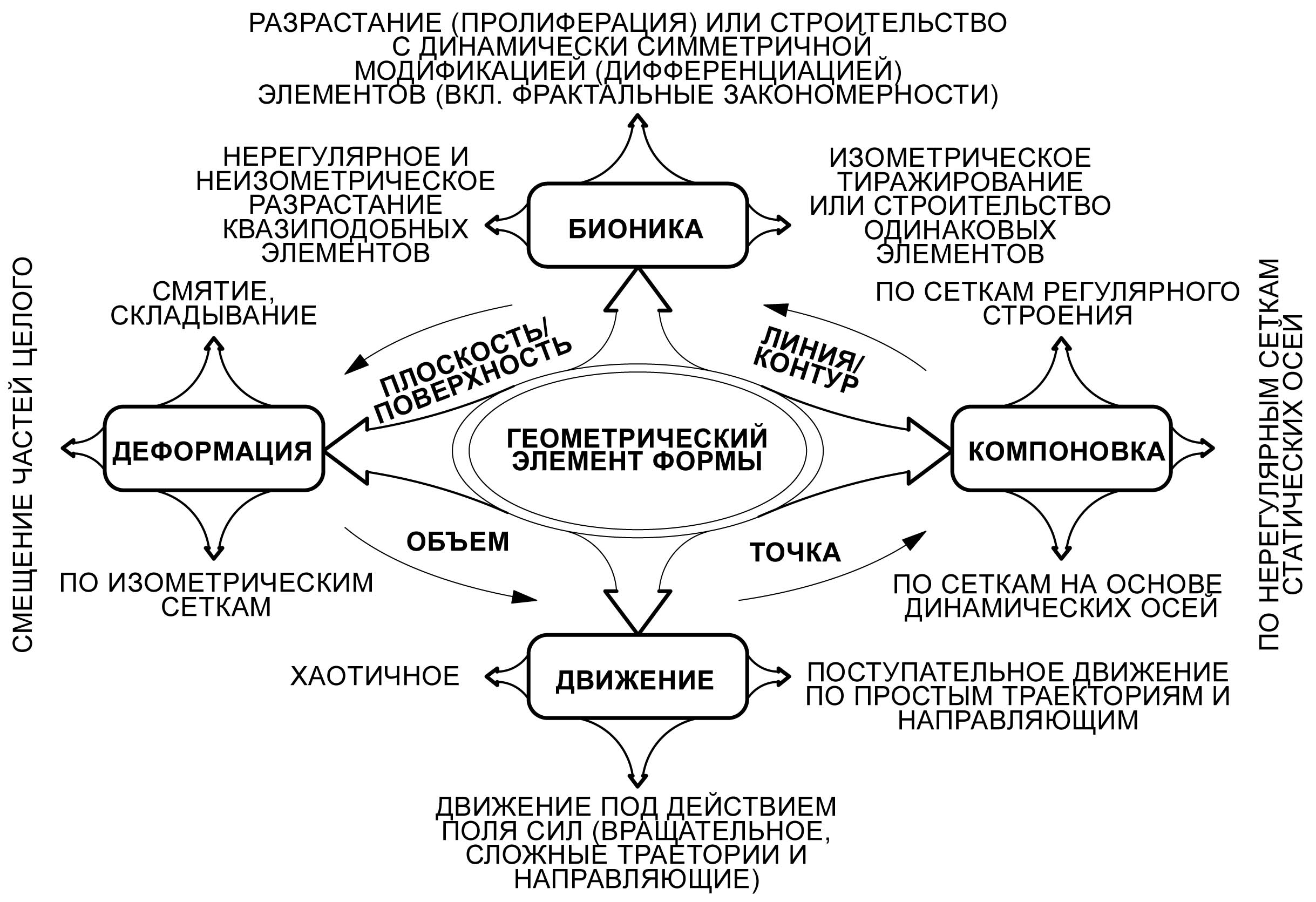

Рис. 16. Схема круговорота природных процессов формообразования.

 

 Рис.17. Цикличность природных моделей формообразования: национальный парк Ленские столбы, Россия.

Продукты природного формообразования можно условно подразделить на регрессивные (в результате деформаций) и прогрессивные (результат роста и упорядоченной компоновки). Первые являются, как бы своеобразным конечным результатом, а вторые – промежуточным состоянием и исходным материалом для продолжения процесса формообразования. Так, листья, упавшие с дерева являются в своей совокупности окончательной формой после трансформации при разложении, что и свидетельствует о регрессивном начале формообразования. Семена, также упавшие с дерева, являются исходным материалом для следующего формообразующего процесса. При этом следует отметить, что структура формы дерева практически повторяется, хотя это не то же самое дерево. Семечко, как результат природного формообразования, благодаря заложенному в него генетическому коду повторяет процесс « построения» новой формы в соответствии с новыми условиями роста. Это говорит о цикличности формообразования и его прогрессивном начале в данном случае. Рассмотренные особенности природного построения форм могут быть переложены на язык архитектурного неоптимизированного формообразования.

Два основных метода архитектурного формообразования графически представляются в виде алгоритмов синтезации и трансформации.

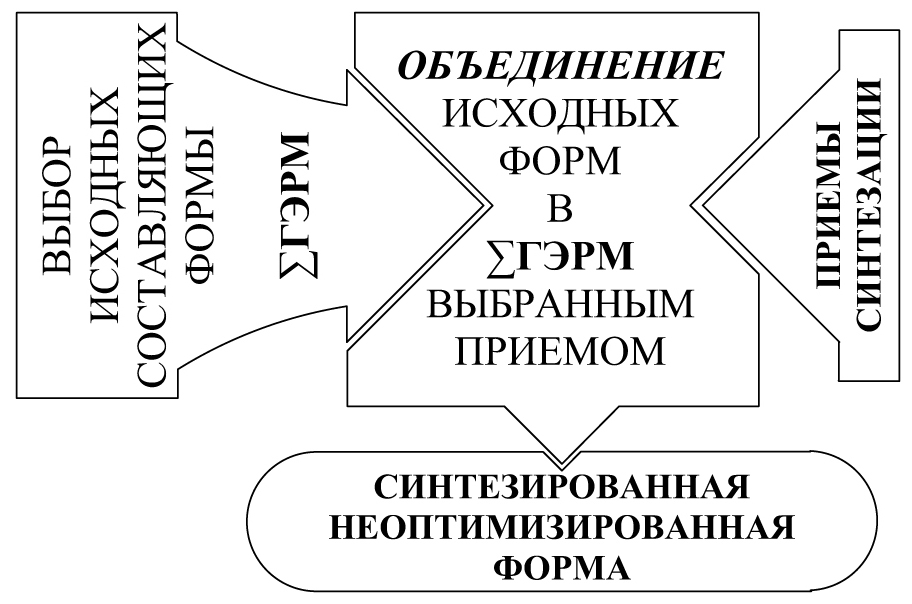
Рис. 18. Алгоритм метода синтезации.

 

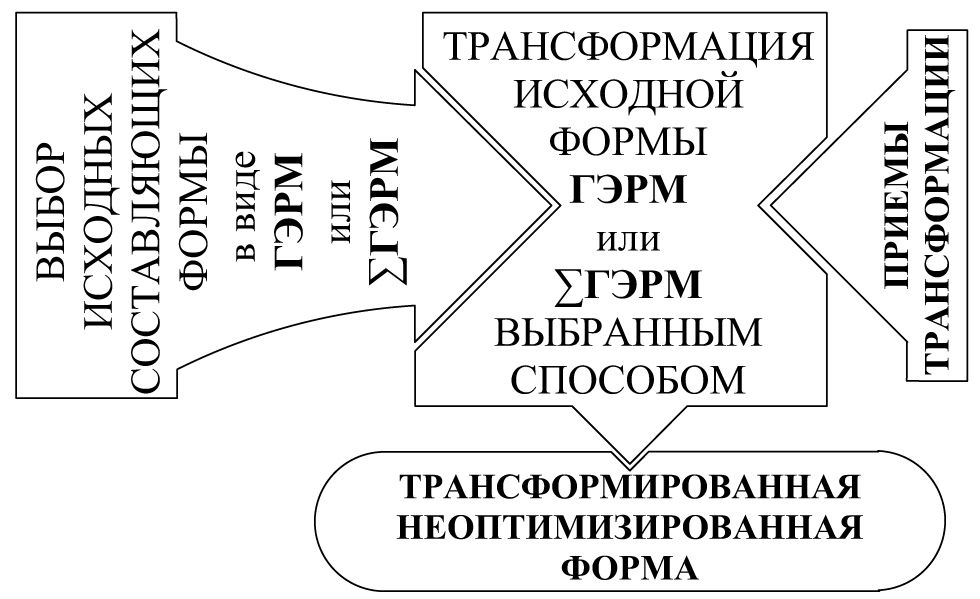
Рис. 19. Алгоритм метода трансформации.

Выполнение первой операции в алгоритме метода синтезации осуществляется произвольно, согласно предпочтениям архитектора или случайно из определенного набора визуализированных геометрических элементов. Принцип цикличности, выявленный в природном формообразовании, происходящий от первоэлемента до целого и в обратной последовательности, позволяет выразить метод синтезации в матричной форме в виде морфера с определенной кодировкой потенциальных форм. Кодировка форм заимствована из тех первоэлементов формальной композиции, беспредметные ассоциации на основе композиций которых изучались в Баухаузе, Вхутемасе и ИнХУКе Иттеном, Гропиусом, Кандинским, Ладовским, Малевичем и другими. Это точка, линия, контур, плоскость, объем. Матрица - морфер позволяет конструировать варианты их формально-композиционных отношений и структур на основе этих отношений. Стоит заметить, что первоэлементы формальной композиции не случайно являются в одно и тоже время концептами математики - геометрии. Сами концепты геометрии, о чем свидетельствуют их научные определения, в свою очередь, являются конструктами - абстракциями, то есть обобщениями на основе рефлексогенной природы представления человека о пространстве, времени и явлениях, происходящих в пространственно-временном континууме.

То есть и в отношении познания природной среды, и в отношении композиционного архитектурного моделирования искусственной среды, понятия точки, линии, контура, плоскости (поверхности), объема являются не абсолютными величинами, но лишь инструментами, в одном случае, анализа, в другом конструирования и художественного синтеза.

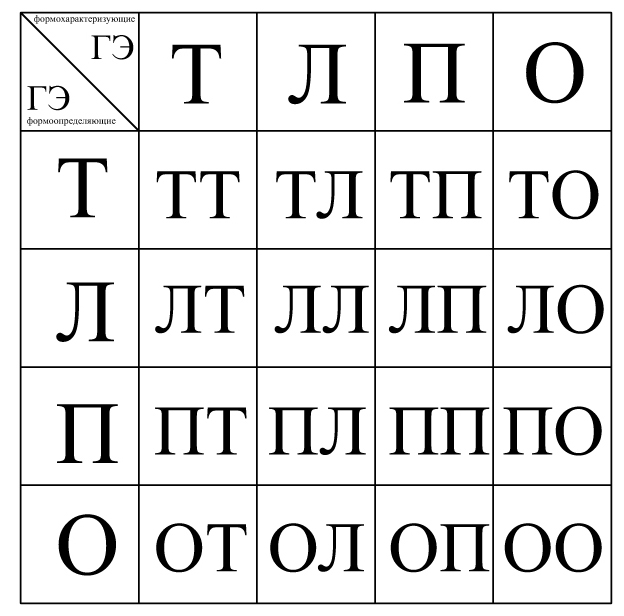
    Рис. 20. Матричная форма морфера 1-го порядка.

 

Верхняя строка и левая колонка данной матрицы содержат перечень первичных элементов предполагаемых ГМФ. В кодированной форме они обозначаются начальными буквами слов: точка, линия, поверхность и объем. В остальных ячейках матрицы спаренными буквами обозначаются возможные ГМФ, причем в каждой строке располагаются формы, производные от исходных элементов левой колонки, являющихся формообразующими. Элементы верхней строки выступают как формохарактеризующие. Таким образом, ГМФ производные, например, от точки обозначаются как точечно-точечные, точечно-линейные, точечно-поверхностные и точечно-объемные.

Морферы следующих порядков образуются на базе использования ГМФ предыдущего порядка в качестве формообразующих совокупностей. Матрица морфера 2-го порядка содержит, при этом, в четыре раза большее число производных ГМФ по сравнению с предыдущей системой. Они рассматриваются в случае ТТ-ной совокупности как точечно-точечные точки и т.д.

Таким образом, рассмотренные особенности и возможности неоптимизированного формообразования в природе и архитектуре существенно расширяют познания в этой области и свидетельствуют о ее неполной изученности.

Комбинаторика, как наука, возникла из теории игр, т.е. в общем берет начало в игре в кости, как и теория вероятности. Поэтому к архитектурной комбинаторике следует относиться, с одной стороны, как к науке, т.к. профессиональный рост без научной базы немыслим, а с другой стороны -как к увлекательной интеллектуальной и, одновременно, интуитивной игре, своеобразной разновидности «игры в бисер» Г.Гессе.

Рис.21. Ченьжень, Китай, Отель и апартаменты Мэйллен, 2011, Urbanus : фасад, созданный на основе применения приемов синтезации.

 

Лекция 3.

Таблица 2.

Доказательство того, что существует ровно пять правильных выпуклых многогранников через рассмотрение развертки вершины такого многогранника.
1	2
Каждая вершина может принадлежать трем и более граням. Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол такого треугольника равен 60°, три таких угла дадут в развертке 180°. Если склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.	Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.
	Три пятиугольные грани дают угол развертки 3*72°=216 - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360° - поэтому останавливаемся.
	Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует. Таким образом, можно убедиться, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.

Платоновыми телами называются правильные однородные выпуклые многогранники, выпуклые многогранники, все грани и углы которых равные правильные многоугольники.

Рис. 23а. Призмы.	Рис.23б. Антипризмы.

 

Равные многогранные углы и правильные грани нескольких типов имеют тела из двух бесконечных семейств - призмы и антипризмы (последние также называют скошенными призмами).

Формы, на основе правильных многогранников и призм активно применялись в архитектуре на протяжении тысяч лет.

Рис. 24а. Идеальный город эпохи Возрождения.	Рис. 24б. Вид сбоку, план, монтаж жилого дома «Димаксион» 1940 е гг. XX века.		Рис. 24в. Эскиз жилья «Димаксион» на 20 рабочих для русского колхоза, 1931 год.

 

Примером здания на основе многогранной призмы в 1940-х годах стал дом из серии «Димаксион» Р.Б. Фуллера. Здание обеспечивало комфорт, оставаясь изолированным от внешних источников энергии и опасностей внешней среды. Основная часть требований была решена за счёт конфигурации здания: по форме походило на юрту. Каркас пола, сделанный из спиц наподобие велосипедного колеса укреплен  на вертикальной оси над землей. Дом был неподвижной конструкцией, вращалась только ветряная турбина на крыше - источник энергии. Образец был построен в 1946 году в Уичито,  Канзас, но автор наотрез отказался от массового производства, хотя один экземпляр стоил бы как автомобиль. В 1998 году в музее Генри Форда в штате Мичиган постоянное место заняла копия дома Dymaxion Фуллера. Небольшой вес домов Фуллера стал легендой. Когда он познакомился в 1970-е годы с Н. Фостером, то спросил: «Сколько весят ваши дома?»

 

Рис.254а. Семейство архимедовых тел: полуправильных выпуклых многогранники (родственны платоновым телам архимедовы тела)	Рис.25б. Правильные однородные звездчатые звездчатые многогранники тела Кеплера-Пуансо
Рис. 26в. Правильный неоднородный выпуклый многогранник в качестве малой архитектурной формы: преобразованный архимедов усеченный кубооктаэдр.	Рис. 26г. Мозаика в соборе Св. Марка в Венеции, иногда приписывается Раоло Уччелло.

 

Существует 13 или 14 архимедовых тел (псевдоромбокубоктаэдр иногда не причисляют к этому семейству). У них все многогранные углы равны, все грани - правильные многоугольники, но нескольких различных типов. Платоновым телам близки тела Кеплера-Пуансо, или правильные однородные невыпуклые многогранники.

У правильных многогранников все грани — равные правильные мно­гоугольники, и все многогранные углы равны. У полуправильных многогран­ников многогранные углы тоже равны, грани являются правильными не равными многоугольниками. Пер­вые 5 тел получаются из правильных многогранни­ков отсечением плоскостями углов многогранника: усеченный тет­раэдр, усеченный икосаэдр и т.д. Дру­гие тела Архимеда носят более слож­ные названия: кубооктаэдр , икосо-додекаэдр , усеченный кубооктаэдр , усеченный икосододэкаэдр , ромбокубооктаэдр , ромбоикосодо-дэкаэдр , «курносый куб» , «курносый додэкаэдр» .

 

 

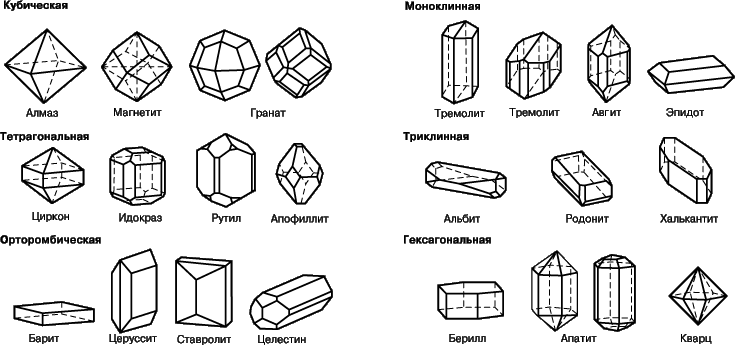
Рис.27. Структуры решеток кристаллов, схожие со структурами полуправильных выпуклых многогранников: «природа не пользуется декартовой системой координат.

 

Широкому внедрению в архитектуру выпуклые многогранники обязаны Р.Б. Фулеру, называвшему свои изобретения артефактами,  явлениями "второй природы".
Самый известный его "артефакт" - геодезический купол (Geodesic Dome). - это сфера или ее сегмент с несущей конструкцией, образованной решеткой из треугольных (или, в более общем случае, многоугольных) элементов. Такая структура позволяет перекрыть огромные площади без использования внутренних опор, обеспечивает максимальную прочность и жесткость при минимальных материальных затратах, причем с увеличением размера сооружения удельные затраты сокращаются.
В настоящее время в мире сооружено более трехсот тысяч "геодезических куполов", не считая игровых конструкций, которые можно часто видеть на детских площадках. К числу наиболее знаменитых относятся купол, установленный на Южном полюсе, великолепный "Золотой купол" Американской выставки в Сокольниках в Москве в 1959 году, ажурный павильон США на Всемирной выставке в Монреале 1967 года высотой более 60 метров и диаметром 75 метров.
Один из проектов Фуллера предусматривал перекрытие огромным куполом всего "даунтауна" нью-йоркского Манхеттена; по прикидкам, стоимость сооружения купола должна была окупиться за несколько лет только за счет сокращения затрат на уборку снега.

"Геодезические купола" достаточно дешевы, легки в сборке, на практике доказали способность выдерживать порывы ураганного ветра скоростью до 210 миль в час, в собранном виде легко перебрасываются по воздуху; их охотно используют в труднодоступных районах. По мнению многих ученых, первые складские и жилые сооружения на поверхности Луны, Марса должны будут сооружаться именно в виде "геодезических куполов". Принцип "геодезического купола" широко используется в современной архитектуре. Прямые цитаты из Фуллера можно найти во многих наимоднейших проектах, в т.ч. в проектах Н. Фостера, сотрудичавшего с Фулером.

Идея "геодезических куполов" явилась результатом интереса Фуллера к картографии, переносу контуров с элипсоидальной поверхности глобуса на плоскость карты с минимальными искажениями. В 1942 г. Фуллер получил первый в истории патент на способ переноса с минимальными искажениями полного изображения с шаровидной поверхности на плоскость.

Идея оказалась в такой степени классически простой, что могла быть предложена в эпоху Возрождения: глобус представал в виде правильного многогранника, одного из пяти платоновских простых тел, а именно в виде икосаэдра, то есть двадцатигранника с гранями в виде правильных, равносторонних треугольников. Эти грани затем разворачиваются на плоскости, давая изображение всей поверхности в целом. Недостатком изображения является невозможность наложить на него привычную координационную сетку; геодезические линии кратчайшего расстояния между точками на поверхности превращаются в ломаные, искажаясь. Поэтому столь невелика была вероятность изобретения подобной картографической проекции в прошлом, когда от карты требовалась в первую очередь возможность ее использования для конкретных задач навигации - на море, на суше или в воздухе. Проекция Фуллера преследует иные цели - она дает возможность "глобального" обозрения поверхности Земли с близким к истинному изображением архипелага суши, позволяет лучше представить глобальную циркуляцию океанских и воздушных течений. Именно такое изображение Земли позволило Фуллеру сформировать, а затем и обосновать гипотезу о вероятных кругосветных путешествиях древних, корабли которых подгонялись морскими и воздушными течениями.
Вслед за Платоном и Эйлером Фуллер увлекся общей теорией многогранников. Результатом этой работы явилось появление своего рода их "периодической таблицы". Через теорию многогранников Фуллер, в частности, обосновывал и периодичность таблицы элементов Менделеева, связывая ее "восьмеричную" структуру с октаэдром и его производными формами.

 

Рис.28а. Купол «Климатрон» в Сент-Луисе в Миссури, 1960 год.	Рис.28б. Геодезический купол на Голливудских холмах - повторение купола, построенного в Монреале в 1950 году.
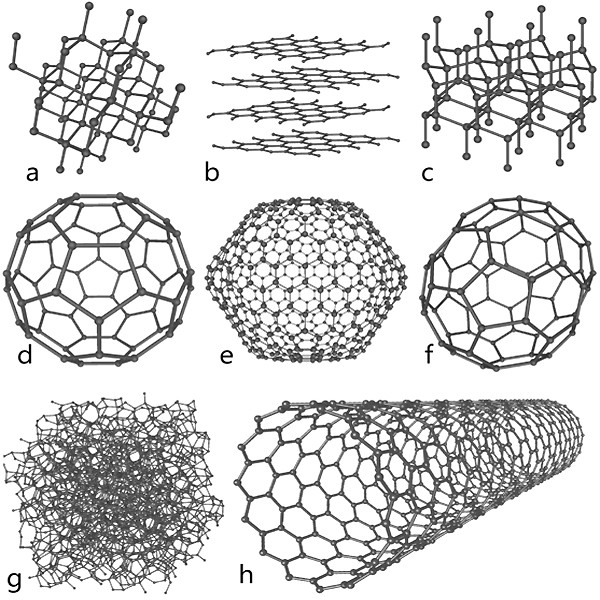
Рис.28в. Аллотропные формы углерода: a: алмаз, b: графит, c: лонсдейлит d: фуллерен — бакибол C60, e: фуллерен C540, f: фуллерен C70 g: аморфный углерод, h: углеродная нанотрубка.	Рис.28г. Биосфера Фуллера (Павильон США на Экспо-67, ныне музей «Биосфера» в Монреале, Канада) Климатрон" (оранжерея) в Ботаническом саду Сент-Луиса (штат Миссури, США)

 

Ричард Бакминстер (Баки) Фуллер - философ, математик, инженер, историк и поэт (дважды отчисленный из Гарварда "за недостаточную тягу к знаниям") изобрел и запатентовал геодезический купол в 1951 году. Предвидя строительный бум, и истощение земных ресурсов по причине увеличения популяции Землян он изобретал пути достижения наибольших результатов, с наименьшими затратами труда и материалов. Фуллер утверждал, что открытая им модель показывает механизмы работы самой природы, которая не пользуется декартовой системой координат, и предложенная им модель может быть моделью расположения атомов в молекуле, которые не вращаются вокруг центра равномерно, а совершают квантовые скачки от одной вершины многогранника к другой. Он оказался отчасти прав: в 1985 г., через два года после смерти Фуллера, ученые Р. Кёрл, Х. Крото и Р. Смоли действительно открыли молекулу углерода предсказанного Фуллером строения. Молекулу назвали фуллерен в его честь, а открывшие ее исследователи в 1996 году получили Нобелевскую премию по химии.

Запатентовав геодезические купола, Фуллер стал продавать лицензии на строительство за 5%, за 30 лет в мире было выстроено около 50 тыс. куполов. Став в конце 60-х наставником новых поколенийон вошел в историю как гуру хай-тека. Ренцо Пиано, автор Центра Помпиду, испытал сильнейшее влияние Фуллера, особенно заметное в ранних его работах, где мысль, фонтанирующая необычными идеями, подчиняет себе инженерные расчеты. Около 15 лет работал вместе с Фуллером Норман Фостер, один из видных архитекторов наших дней.
Еще одним важным вкладом Фуллера в архитектуру и строительство явилась теория так называемых тенсегритных структур. В их основу заложено понятие, которое может быть приблизительно переведено как "напряженная целостность", когда элементы, подверженные сжатию, не соприкасаясь, формируют общую структуру, соединенные между собой тонкими растяжками, которые несут стягивающие "синтропические" (направленные внутрь) силы. На этом принципе Фуллером был разработан проект телетрансляционной башни высотой 3736 метров для японской телевизионной компании - выше горы Фудзияма (высота существующих телебашен не превышает 600 метров).
"Геодезические купола" и "тенсегритные конструкции" явились частным случаем применения геометрической теории многогранников, которые были любимым объектом исследований Фуллера. 

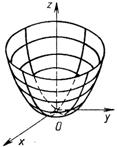
2 группа - включает все тела вращения и формы, образованные криволинейными поверхностями (шар, цилиндр, конус, формы с параболическими и гиперболическими поверхностями и т.д., см. таб. 3).

Примерами использования геометрических тел этой группы в архитектуре являются работы инженеров Владимира Шухова и Бакминстера Фуллера, Фрай Отто, С. Калатравы, З. Хадид.

 

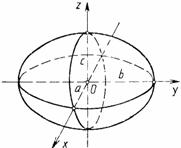
Таблица 3.

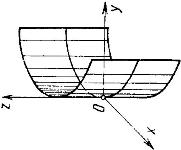
Эллипсоид	Эллиптический параболоид
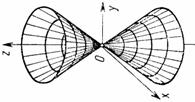
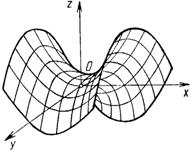
Конус второй степени	Гиперболический параболоид
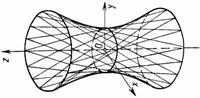
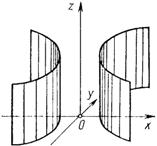
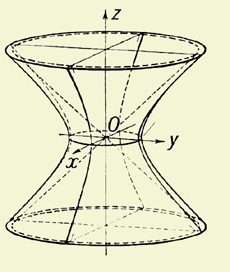
Однополостный гиперболоид	Эллиптический цилиндр
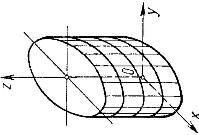
Двуполостный гиперболоид	Гиперболический цилиндр Параболический цилиндр

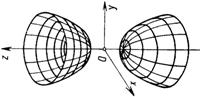
Рис.29.. Пример использования геометрических тел 3 группы в архитектуре – Башня на Шаболовке по проекту инженера Владимира Шухова.

 Башня для радиостанции в Москве на Шаболовке, построенная по проекту русского инженера, почётного академика В. Г. Шухова, состоит из звеньев - гиперболоидов вращения. Каждый из них изготовлен из прямолинейных металлических стержней, соединяющих соседние окружности.

Рис.30а. Дом Димаксион закончен в 1929 г. и был пересмотрен в 1945 г., хотя разработки начались в 1927 г.
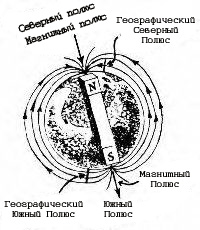
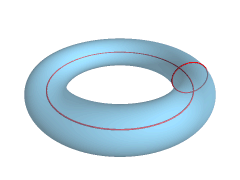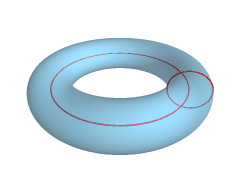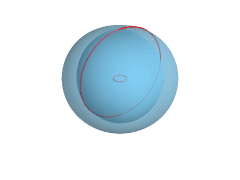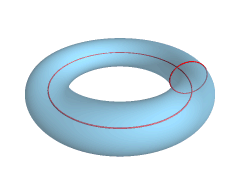
Рис.31б. Тор - поверхность, образованная вращением окружности вокруг оси, принадлежащей плоскости окружности, но не проходящей через ее центр. Ось вращения может пересекать окружность, касаться ее и располагаться вне окружности. В первых двух случаях тор называется закрытым, в последнем - открытым, или кольцом.		Рис.31в. Тор (тороид) образуется магнитными линиями Земли, которая, в свою очередь является эллипсоидом.
Рис. 32. Геометрический вид структур, возникших в результате падения на Луну астероида, близок в эллипсу: природоподобной структуре.
Ударный кратер на территории Моря Дождей на Луне, включающий первичные (исходящие от кратера) и вторичные канавы. D территории кратера и канав достигает 1250 км, d  столкнувшегося с Луной объекта - 80 км. Геофизики полагают, что на ранних этапах развития Солнечной системы окрестности Венеры, Земли и Марса содержали множество протопланет (крупных астероидов).

 4 группа – бесчисленное количество сложных стереометрических фигур, имеющих прямолинейные и криволинейные поверхности.

Рис. 33. Поверхности вращения третьего и более порядка: зачастую симметрия касается только отдельных частей: начинает активно проявляться свойство нелинейности уравнений таких поверхностей.

Поверхности такого порядка используют в архитектуре З. Хадид и Френк Гери, хотя поверхности архитектурных форм Гери не генерируются, а только просчитываются дигитально, их конфигурация задается параметрически.

Архитектурная математикаВ Лондоне, Англия, открыла двери для посетителей Галерея Уинтон: Математика, являющаяся частью Музея науки. Это первый на территории Великобритании проект, осуществлённый студией Zaha Hadid Architects после смерти главы компании. Сама Заха Хадид до начала своей архитектурной карьеры изучала математику в Американском университете Бейрута. Поэтому не случайно работы её фирмы отличаются сильными геометрическими формами, основанными на глубоком понимании математических законов.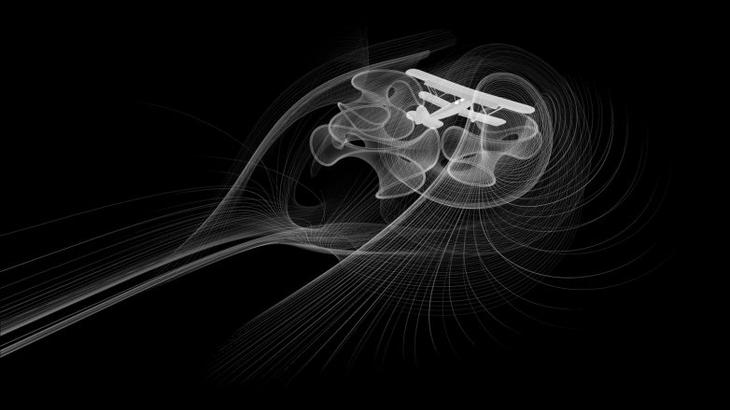

 

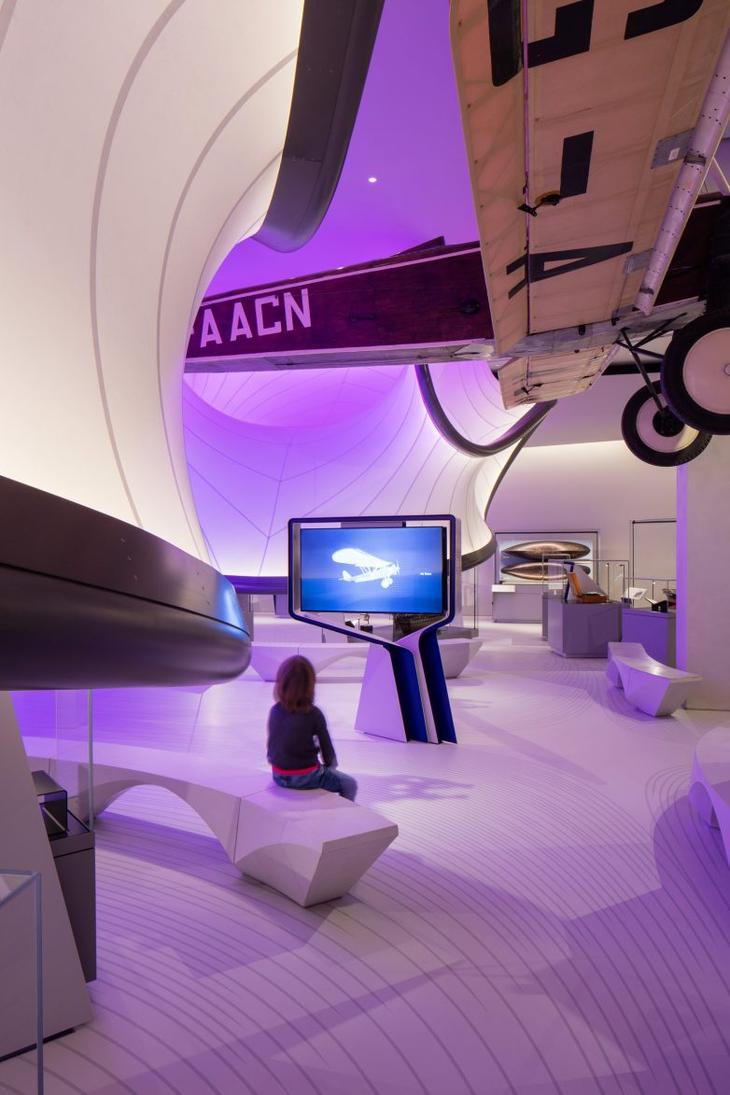
«Когда я росла в Ираке, математика была для меня частью повседневной жизни. Мы играли с математическими задачами так же, как мы играли с ручками и бумагой, когда рисовали. Математика была как рисование», — рассказывала Хадид о своём детстве. Так же и куратор галереи Дэвид Руни стремился представить математику не как академическую дисциплину, но как практику, влияющую на окружающую нас технику и трансформирующую жизненную среду человека. Текучие поверхности, формирующие пространство галереи, визуализируют аэродинамическое турбулентное векторное поле, создаваемое самолётом, помещённым в центр экспозиции. Аэроплан авиаконструктора Хэндли Пейджа, отличившийся в конкурсе 1929 года Guggenheim Safe Aircraft Competition, стал знаковой вехой в развитии гражданского воздухоплавания, сделав этот вид транспорта доступным для простых людей. Среди экспонатов также представлены исламская астролябия XVII века, машина Энигма и ранний образец системы искусственного интеллекта — всего более 100 исторических объектов. Само пространство галереи, его наполнение, включая произведённые с помощью роботов крепкие арочные скамьи — всё воплощает математический дух. Полученный в результате посещения выставки опыт позволяет людям увидеть лишь некоторые из множества реальных и осязаемых способов, которыми математика соприкасается с нашей жизнью. https://udivitelnoe.temaretik.com/1075857306419202584/arhitekturnaya-matematika/

Хотя сложные криволинейные поверхности использовали исторические стихи барокко и рококо, однако это были поверхности архитектурных деталей, которые моделировались в скульптурной пластике в масштабе 1:1,  а затем отливались или изготавливались в мраморе, конфигурация поверхности переносилась по точкам, методом триангуляции.

Огромный вклад в архитектурное формообразование внес русский инженер Владимир Шухов - создатель сетчатых мембран – перекрытий (см. рис 34).

Рис.34. Первая в мире стальная мембрана-перекрытие: ротонда по проекту инженера Владимира Григорьевича Шухова на Всероссийской промышленной и художественной выставки 1896 года в Нижнем Новгороде
Рис.35. Моделирование форм и структур «тенсегрити», по Б. Фулеру.

 

В архитектурной деятельности наиболее употребительна первая группа фигур – кубы и параллелепипеды.

Каменное строительство и протоархитектура зародились в неолите, при переходе к оседлому земледельческому образу жизни в VII-VI тыс. до н.э.. Первые сооружения жилого и культово-астрономического из мелкоразмерного камня имели форму, близкую к круглой (Руджим эль Хири и др.), планировки поселений -  нерегулярную структуру, базирующуюся на центрической радиальной (эль Хири) либо свободной композиции близких к окружностям структур (Хирокития, таб.4).

Возросшая плотность поселений и потребность деления круга на сектора для получения плотных «упаковок» пространства определила эмпирический процесс приближения к прямому углу в отдельных сооружениях (пос. на Оркнейских о., таб 4.), а затем и его преобладание в структуре протогородов (Чатал Куюк- таб.4).

 

Таблица.4. Геометрия архитектуры неолита.

Неолит. Хирокития. Кипр. VII-VI тыс. до нашей эры: постройки поселения не имеют ни одного прямого угла.	Шотландский остров Мейнленд. В западной части острова памятники неолита Оркнейских островов: руины, включающие погребальную камеру и хорошо сохранившееся поселение эпохи неолита : план поселения в основе круг, разделенный «секторами».	Чатал-Гуюк крупнейшее поселение эпохи керамического неолита и энеолита в Гамирке. Культурные слои  7400 г. до н. э. - 5600 г. до н. э. Жители покинули поселение до наступления Бронзового века: упаковка из прямоугольных домов без улиц.

Прямоугольные структуры обладают следующими уникальными для применения в архитектуре свойствами (рис.35):

- прямоугольные структуры наиболее удобны для организации жизненных процессов и ориентации человека в пространстве;

- прямоугольные элементы легко объединяются в группы;

- внутреннее пространство ортогональных форм нетрудно разделить на подобные им пространства меньших размеров;

-вертикальные и горизонтальные плоскости таких форм соответствуют наиболее развитой стоечно-балочной конструктивной системе. 

Формы других стереометрических тел весьма трудно сочетаются между собой.

Их применение эффективно лишь в особых случаях, при создании формы крупных единичных объектов.

 

Лекция 4.

Таблица.6.

1.	Принцип целесообразности	эстетическая, функциональная, конструктивная)
2.	Принцип единства сложного	целостность произведения, архитектоника
3.	Принцип доминанты	наличие главного, ведущего начала
4.	Принцип иерархии	соподчинения частей в целом
5.	Принцип динамизма	движение — основа жизни и искусства
6.	Принцип равновесия	уравновешенности частей целого
7.	Принцип гармонии	гармоническое единство элементов формы между собой и единство формы и содержания в композиции на основе диалектического единства противоположностей

Цельность – эмоциональная оценка формы, зависящая от соподчиненности признаков всех ее элементов, из которых состоит целое. При членении квадрата на две равные части его форма теряет цельность из-за крупности элементов и их значительной  самостоятельности. При этом, элемент членения динамичен, тогда как исходный квадрат статичен.

Эмоциональная оценка первичного признака формы ее геометрического вида дает такие вторичные признаки как динамичность, статичность и мерность.

Динамичность – эмоциональная оценка изменения, точнее нарастания массы или пространства внутри границ формы, преобладающего в каком либо направлении ее развития. Динамичность может иметь разный характер: композиционно-визуальный и композиционно-технологический.

Степень динамичности – вторичный признак формы, выражающий степень изменения визуальной массы, а также степень ее концентрации в каком либо направлении. Степень динамичности и степень статичности – обратно пропорциональные величины. Их значения рассчитываются с помощью технических и программных средств машинной графики. Границы любой формы можно представить как результат действия сил сжатия и растяжения. Направления действия этих сил, в которых степень динамичности достигает экстремальных значений, называются динамическими осями. Динамическая ось, по линии которой степень динамичности максимальна, называется главной динамической осью. В случае, если форма имеет несколько динамических осей с максимальной степенью динамичности, то за главную ось зрительная система человека принимает горизонтальную, а при ее отсутствии вертикальную ось. Следует отметить, что окружность и шар обладают бесконечным множеством динамических осей, а степень динамичности их в любом направлении является постоянной. Точки пересечения динамических осей называются композиционными центрами. Точки изменения направления движения глаз наблюдателя по контуру плоских фигур называются информативными точками.

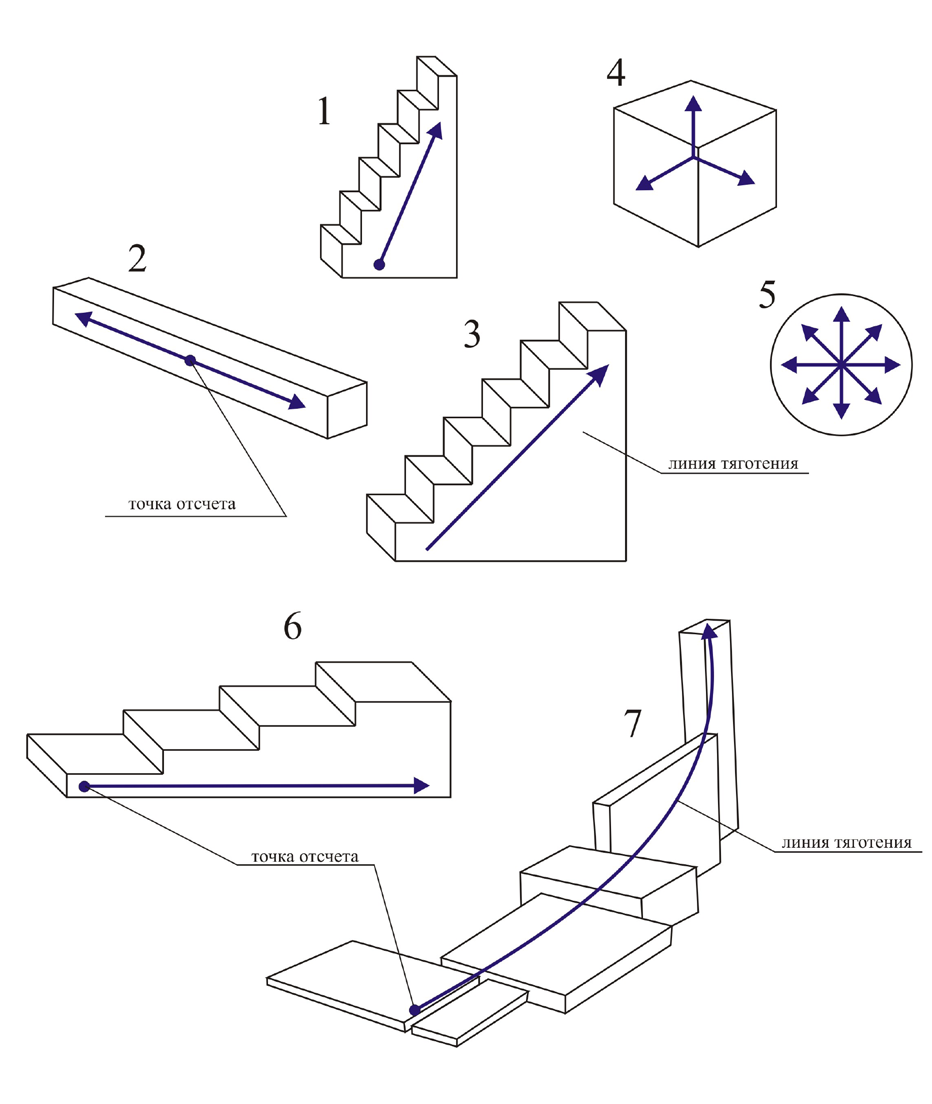
Рис. 51. Суммарные векторы динамичности элементов архитектурной формы, архитектурных форм, городского пространства. 

Статичность – эмоциональная оценка неизменяемости массы или пространства внутри границ формы по всем направлениям ее развития.

Величина – рассматривается как соотношение протяженностей формы по трем координатам, как соотнесение двух или более форм между собой (большая - меньшая) и по отношению к человеку. Пределами ряда форм по величине будут равенство сопоставляемых форм или минимальные размеры одной формы по отношению к другой, когда обе формы ясно воспринимаются. Величина формы является продуктом ее относительной оценки и возникает в процессе восприятия благодаря его целостности и соотносительности. Целостность означает единство процесса восприятия, как целого, так и его частей одновременно. Соотносительность – особенность восприятия, выражающаяся в том, что все признаки одних объектов воспринимаются в сравнении с такими же признаками других объектов.

Масштаб – эмоциональная оценка членения формы, выражающая степень крупности элементов формы по отношению к форме в целом, а также между совокупностью форм. В соответствии с этим формы бывают крупномасштабные, среднемасштабные и мелкомасштабные.

Визуальная масса – эмоциональная оценка тяжести формы, которая прямо пропорциональна количеству материала и его плотности. Она характеризует силу воздействия формы на зрительный анализатор и зависит от соотношения ее периметра и площади, от ориентации, размеров и ряда других первичных признаков. Элемент формы, имеющий наибольшую визуальную массу, является, как правило, ее главным элементом.

Мерность – эмоциональная оценка соотношения параметров формы, ее объемности, поверхностности, линейности и точечности.

Формы согласно мерности. Формы согласно мерности называются трехмерными, двухмерными, одномерными и нольмерными.

 Отношения – количественное выражение первичного признака формы – геометрического вида в числовых соотношениях. Они определяют параметрическую заданность формы, как своеобразный числовой код. Так, например, отношение 2:3 определяет получение прямоугольной формы и предполагает ее мысленное расчленение на шесть квадратов. Отношения представляются как целыми рациональными, так и иррациональными числами. Иррациональное отношение 1:√2 характеризует построение прямоугольника с одной из сторон в виде диагонали квадрата.

В математической равенство двух отношений выражается формулой a:b=с:d, и каждый член ее может быть определен через остальные три. В гармонической пропорции - 3 элемента. Они являются или попарными разностями некоторой тройки элементов, или самими этими элементами, например:

а:с=(а - в): (в - с)

В геометрической пропорции тоже всего 3 элемента, но один из них общий, а:в=в:с. Разновидностью геометрической пропорции является пропорция так называемого "золотого сечения", имеющая всего два члена - "а" и "в" - излюбленная пропорция художников, которую в эпоху Возрождения называли "божественной пропорцией".

Золотое сечение (з. с.)

Особенностью пропорции золотого сечения является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т. е.

а:в=в: (а -в)

§ Отношение «золотого сечения» выражается числом 0,618.

§ Пропорция «золотого сечения» 1:0,618=0,618:0,382.

Если отрезок прямой выразить через единицу, а затем разделить его на два отрезка по соотношению «золотого сечения», то больший отрезок будет равен 0,618, а меньший 0,382.

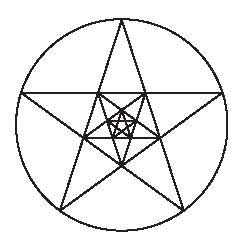
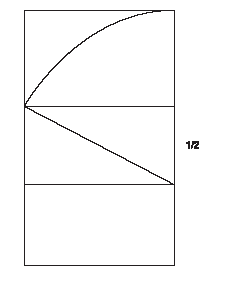
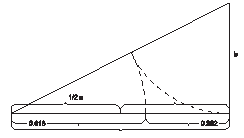
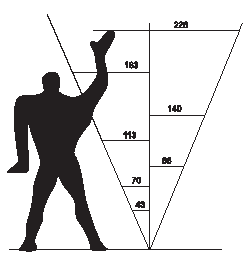
Рис.53. Схемы построения отношений золотого сечения.

Пропорционирование - приведение частей целого к единому пропорциональному строю. исследование использования золотого сечения нес свой вклад Джей Хэмбидж. В 1920-м г. в Нью-Йорке вышла его книга "Элементы динамической симметрии". Хэмбидж исследовал динамическую симметрию, которую он обнаружил в ряде прямоугольников, с целью ее практического применения художниками в композиционном построении. Он делает попытку раскрыть секреты, которыми пользовались древние греки, добиваясь гармонического решения формы. Его внимание привлекли свойства прямоугольников, составляющих ряд, где каждый последующий прямоугольник строится на диагонали предыдущего, начиная с диагонали квадрата Ц2. Это прямоугольники Ц4, Ц5 (с меньшей стороной равной стороне квадрата, принятой за единицу). (Рис. 17). Кульминацией ряда является прямоугольник Ц5, обладающий особыми гармоническими свойствами и "родственный" прямоугольнику золотого сечения, (о нем будет сказано ниже).

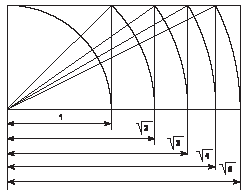
Рис. 54. Ряд динамических прямоугольников Хэмбиджа – аналог последовательности русских саженных мер длины в архитетектуре домонгольского периода.

Хэмбидж рассматривает также площади квадратов, построенных на сторонах этих прямоугольников и обнаруживает следующую динамику: в прямоугольнике  со стороной корень квадратный из 2 квадрат, построенный на большей стороне, имеет площадь в 2 раза большую, чем квадрат, построенный на меньшей стороне. В прямоугольнике Ц3 квадрат на большей стороне в 3 раза больше квадрата на меньшей стороне и так далее. Таким образом образуются динамические ряды площадей, состоящие из целых чисел. Хэмбидж утверждает, что древние греки использовали этот принцип в своих композиционных решениях. Прямоугольники динамического ряда, о котором мы говорили, являются первичными площадями в композиционной системе Хэмбиджа. Каждый из этих прямоугольников может быть разбит на отдельные части и порождать новые композиционные решения, новые темы. Например, прямоугольник Ц5 можно разбить на квадрат и два прямоугольника золотого сечения. Прямоугольник золотого сечения может быть разбит на квадрат и прямоугольник золотого сечения, а также может быть разбит на равные части, при этом обнаруживается следующая закономерность: при делении пополам он даст два прямоугольника, в каждом из которых будет по два прямоугольника золотого сечения. При делении на три части - по три прямоугольника золотого сечения в каждой трети. При делении на 4 части - по четыре прямоугольника «золотого сечения» в каждой четверти основного прямоугольника.

Среди систем пропорционирования, используемых в архитектуре, дизайне, в прикладной графике следует упомянуть системы "предпочтительных чисел" и различные модульные системы.

"Предпочтительные числа" - ряд чисел геометрической прогрессии, где каждое последующее число образуется умножением предыдущего числа на какую-нибудь постоянную величину. Числа из предпочтительных рядов используются при конструировании упаковок, в композиции рекламных плакатов. Они обеспечивают ритмическое развитие формы, их можно встретить и в построении формы античной вазы и в современном станке.

Известна система пропорционирования - так называемые "итальянские ряды", в основе которых лежат первые числа ряда Фибоначчи - 2, 3, 5. Каждое из этих чисел, удваиваясь, составляет ряд чисел, гармонически связанных между собой:

· 2 - 4, 8, 16, 32, 64, и т. д.

· 3 - 6, 12, 24 48, 96

· 5 - 10, 20, 40, 80, 160

Пропорционирование связано с понятиями соразмерности и меры. Одним из способов соизмерения целого и его частей является модуль. Модуль - размер или элемент, повторяющийся неоднократно в целом и его частях. Модуль (лат.) означает - мера. Любая мера длины может являться модулем. При строительстве греческих храмов, чтобы добиться соразмерности использовали также и модуль. Модулем мог служить радиус или диаметр колонны, расстояние между колоннами.

Витрувий, римский зодчий 1 в. до н. э., в своем трактате об архитектуре писал, что пропорция есть соответствие между членами всего произведения и его целым - по отношению к части, принятой за исходную, на чем и основана вся соразмерность, и соразмерность есть строгая гармония отдельных частей самого сооружения и соответствие отдельных частей и всего целого одной определенной части, принятой за исходную.

В прикладной графике модуль широко используется при графическом дизайне, дизайне предметной и архитектурной среды, архитектуре. Применение модульных сеток помогает упорядочить расположение элементов формы, способствует созданию композиционного единства. В основе модульного конструирования лежит комбинация пересекающихся линий, образующих сетку, делящих целое на элементы, предназначенные для распределения текста, геометрических, функциональных и конструктивных элементов формы. Прямоугольный модуль наиболее употребим, один или несколько  определяют ритмически организованное распределение элементов формы.

Светотень – эмоциональная оценка светлоты, выражающаяся в понятиях светлых и темных оттенков в ахроматических отношениях. Светлые оттенки иллюзорно увеличивают и приближают формы к наблюдателю, а темные – наоборот.

Рис. 54. Светотень. 

Лекция 5.

Композиция - некоторое множество элементов, обладающих определенными признаками и находящихся во взаимодействии, характеризующемся субъективно воспринимаемой, но статистически подтвержденной структурной целостностью и эмоциональной выразительностью.

На изучении принципов организации структурно-целостных при субъективном восприятии большинства людей композиций занимается теория формальной композиции. Активная дигитализация архитектурно-проектной и дизайнерской деятельности дала дополнительный толчок развитию теории формально - композиционного формообразования и совершенствованию ее научных методов. Задачей этой научной дисциплины является анализ и разработка общих принципиальных основ гармонически оптимального построения формы архитектурных объектов. Научную основу теории формально – композиционных построений составляет экспериментальная психофизиология зрительного восприятия человека и психология.  Психология определяет совокупность психических процессов человека, обуславливающих его архитектурно – композиционную деятельность.   Психофизиология как раздел физиологии и психологии определяет физиологические механизмы, обеспечивающие реализацию психических процессов и явлений в процессе структурно-композиционного формообразования и восприятия.

Данные этих наук свидетельствуют о том, что восприятие человеком предметно – пространственной среды определяется двумя основными факторами. Первый из них – сенсорный, зависящий от физических параметров стимула, названный еще  В. Фехнером (1876 г.) «объективным фактором эстетического впечатления». Второй фактор определяется как  ассоциативный. Он зависит от мотивов, предыдущего опыта познания и восприятия, установок воспринимающего субъекта. Положение о двухмерности зрительной информации определяет эстетическую оценку в качестве производной меры соответствия состава и структуры воспринимаемого информационного потока анатомическим и психофизиологическим особенностям анализаторам человека и производной соотношения смыслового содержания воспринимаемой информации с эталонами  памяти субъекта восприятия. Первое слагаемое эстетической оценки, приближенно одинаково у различных наблюдателей с нормально функционирующими анализаторами. Второе слагаемое, напротив, всецело обуславливается накопленным опытом человека, его интересами, желаниями, и поэтому оно индивидуально, но область эталонных значений композиции здесь находится в сфере общей культуры общества.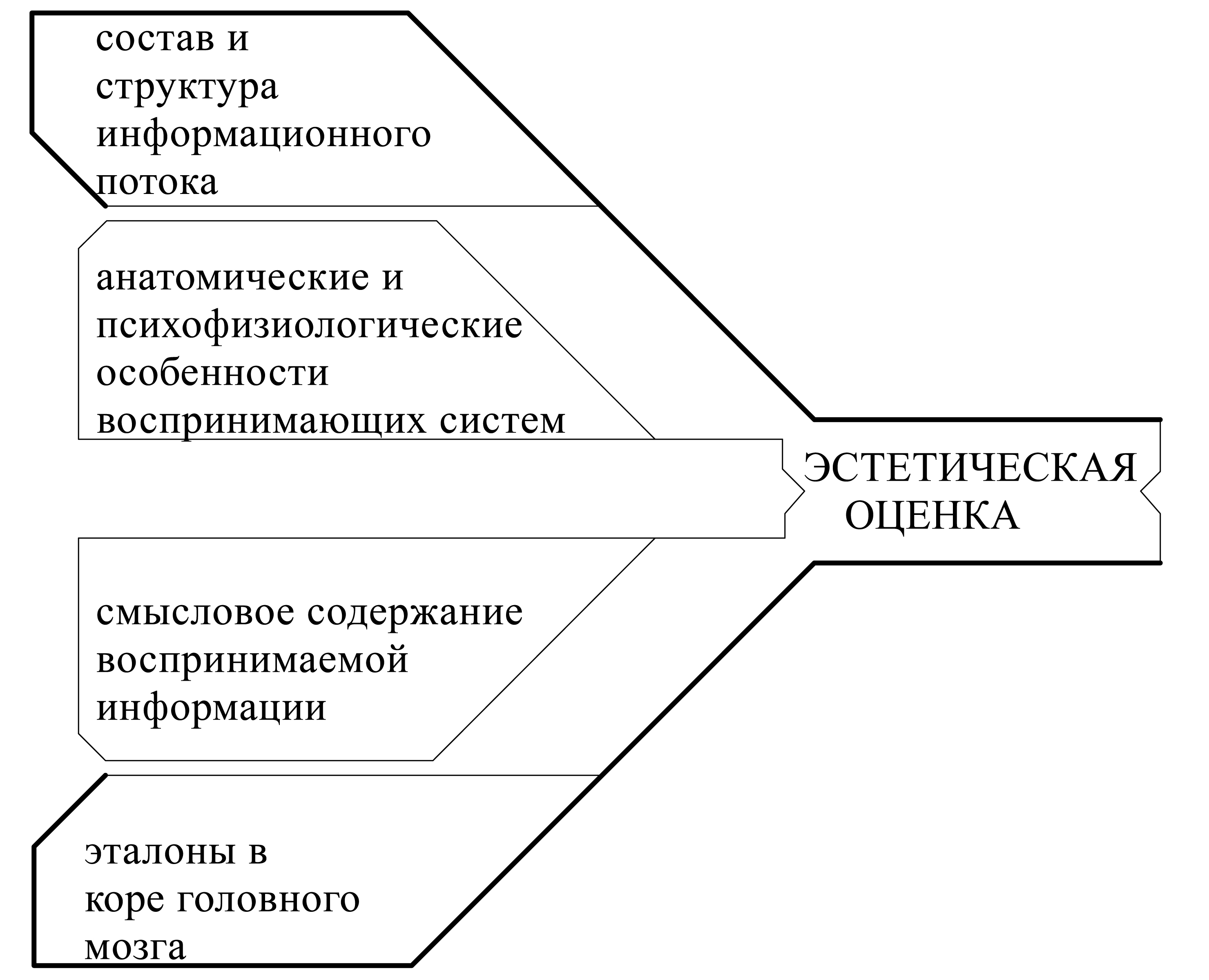

 Рис. 58. Слагаемые эстетической оценки (по А.В. Шаповалу).

 

Первое – формальное, а второе – ассоциативное, опирающееся на особенности функционирования глубинных отделов коры головного мозга человека, определяемое  задачей разработки способов достижения выразительности формы, поиск путей совершенствования смысловой, содержательной стороны композиционных структур, нахождение концептуального начала для создания эксклюзивных форм. В современной теории композиции, согласно исследованиям А.В. Шаповала, определяются два направления: теория формальной композиции и теория ассоциативной композиции. Такой подход к пониманию эстетической оценки позволил выделить и главные направления развития теории формально-композиционного формообразования.

 Многие проблемы теории формально-композиционного формообразования решаются в тесном контакте с психофизиологией зрительного восприятия. Здесь частично используются методы граничащих с ней областей применения средств вычислительной техники – машинной графики, распознавания образов, в перспективе - теории систем.   

Таким образом, эстетическая оценка архитектурной формы наблюдателем – непосредственное следствие степени структурно-композиционного осмысления формы архитектором, дизайнером архитектурной среды. В теории архитектурного формообразования форма понимается как структурно и композиционно осмысленное конечное множество элементов, обладающих определенными признаками и свойствами, «Относительно признака свойство представляет собой более сложную характеристику (по А. В. Шаповалу, свойство есть отношение признаков)». Элемент, при этом, представляет собой составную часть формы, ограниченную одним или несколькими замкнутыми контурами, поскольку все элементы архитектурной формы объемны, либо имеют толщину.

Е. Синицын, О.Синицына

Таблица.9.

Архитектурно-планировочный уровень реализации группы функций		Соответствие уровню визуальной метрической организации
Система город- градостроительный кластер	[0]	шестой «F»	от 100м до 1км
Система – градостроительный кластер	[-1]
Группа подразделений внутри кластера	[-2]
Уровень подразделения	[-3]	пятый «E»	от 10м до 100м
Уровень функционально-планировочной группы	[-4]
Уровень планировочной ячейки	[-5]	четвертый «D»	от 1 м до 10м
Эргономический уровень	[-6]	третий «C»	от 100мм до 1000мм

 

Раздел II. Теоретический.

Лекция 6.

Тема 6.1. Базовые принципы формально - композиционного формообразования.

Среда обитания

Четыре материала будущего: от нанотрубок до паутины

archspeech разбирается в пользе для архитектуры четырех материалов, чей потенциал давно привлекает мировое сообщество.

Кевлар, углеродные нанотрубки, карбонат кальция и синтетическая паутина — четыре очень прочных материала, за которыми с интересом следят профессионалы самых разных сфер деятельности. Их уже активно используют в медицинской и военных целях, и все идёт к тому, что эти материалы в будущем на постоянной основе смогут быть применены и в строительстве.

Вслед за коллегами с портала Archdaily мы изучили документальный фильм «Самые прочные материалы» (World’s Strongest Materials), созданный на одном из самых известных научно-популярных каналов США NOVΛ, и подробнее рассмотрели все четыре материала.

 

Кевлар

Кевлар — ткань из волокна синтетического происхождения, которая в пять раз прочнее стали. Материал был получен еще 50 лет назад и разрабатывался изначально для армирования автомобильных шин. Самое большое применение кевлар пока нашел в бронежилетах, но постепенно захватывает, например, судостроительный рынок, где производители яхт переходят на строительство корпусов полностью из кевлара.

Благодаря особой молекулярной жестокости кевлар на текущий момент считается самым прочным синтетическим волокном в мире. В архитектуре и строительстве прежде всего привлекает его высокий предел прочности на растяжение и долговечность. Применение этой технологии дает возможность снижения веса гибких конструкций вдвое без ущерба для их несущих способностей.

Одним из первых примеров использования кевлара в архитектуре стал Олимпийский стадион в Монреале, открытый в 1976 году. Хотя ничего хорошего тогда из этого не вышло. Из-за сложности технологий сворачиваемая кровля на основе кевлара и башня, поддерживающая ее на тросах, были введены в эксплуатацию только в 1987 году, но уже 11 лет спустя конструкция была заменена из-за множественных повреждений, не выдержав сильных ветров.

Тем не менее, в последнее десятилетие кевлар снова начинает набирать популярность в архитектурной среде. Питер Теста (Peter Testa) разработал прототип 40-этажного небоскреба без единой несущей колонны, который полностью состоит из композитных материалов, закрученных в плотную структуру. Проект успешно выдержал первоначальные расчеты, в том числе с участием инженеров из Arup, а сам автор утверждал, что в ближайшие 5-10 лет постройка таких зданий станет вполне реальной. Пока прогнозы не оправдываются, но с каждым годом кевларовые технологии становятся все доступнее на рынке.

 

Углеродные нанотрубки

В общем виде такие нанотрубки представляют собой мельчайшие цилиндры (хотя длина трубок может достигать нескольких сантиметров), выложенные правильными шестиугольниками, в вершинах которых расположены атомы углерода. Такая структура позволяет им в 100 раз превосходить прочность стали, обладая при этом еще множеством полезных свойств для целого ряда областей науки.

Например, из нанотрубок получилось создать искусственную мышцу, которая в 85 раз сильнее человеческой. Также технологию используют для разработки по-настоящему невидимых объектов. В строительный сфере углеродные нанотрубки видится прежде всего как альтернатива и скорая замена арматуре в составе железобетонных конструкций.

Например, профессор казанского Института физики Ленар Тагиров подтверждает, что прочность пенобетона с добавлением нанотрубок возрастает в два раза, а кирпича — на 40%. К тому же трубки чрезвычайно устойчивы к проявлениям коррозии, так что в будущем бетон, который сам себя ремонтирует, может уже и не пригодиться.

О значительном прорыве для строительной сферы заявляли ученые из австралийского Перта еще год назад. Компания Eden Energy Limited предлагает производить углеродные нанотрубки из газа, что позволит им выйти на действительно массовый рынок. Ученые даже нашли решение проблемы токсичности материала, вызывающей аналогичные асбестовым волокнам последствия. Но пока разработка все еще находится на этапе тестов.

 

Карбонат кальция

Карбонат кальция является составной частью известняка, мрамора и мела, поэтому обычно и не рассматривается в качестве несущего материала. Но природа и процессы эволюции показывают, что у этого вещества и его производных есть перспективы не только для применения в отделке. Особенность материалов, в состав которых входит карбонат кальция, в том, то они способны переносить высокие нагрузки на сжатие, но при этом остаются очень хрупкими. Например, поставленные вертикально несколько пачек мелков или пара бокалов из хрусталя без проблем выдерживают вес человека.

Особый интерес для изучения представляет строение раковины моллюсков, а именно деликатесного вида Abalone. Его раковина больше напоминает и с виду, и на ощупь камень, неподдающийся никакому внешнему воздействию, хотя на 95% повторяет состав мела. Такие свойства стали возможны благодаря уникальному многослойному строению раковины, где атомы кальция, углерода и кислорода находятся в неподвижности благодаря перекрывающим их слоям протеина.

Здания теперь вряд ли начнут строить из ракушек, но их уникальное строение стало поводом для ученых попытаться повторить структуру, которая сможет соперничать по прочности на сжатие с кирпичом, цементом и бетоном. Если все получится, то в бущущем вполне можно ожидать появления настоящих стеклянных небоскребов и подводных городов с обзорными потолками.

 

Паутина

Удивительно, но по прочности на разрыв обычная паутина превышает показатели стали и кевлара, при этом еще и способна растягиваться на 140% от первоначальной длины, не деформируясь и оставаясь подвижной даже в условиях экстремального холода. Понятно, что такой материал пригодится в любой сфере, в том числе и в архитектуре. Вопрос только, как наладить его промышленный выпуск.

Самое большое полотно из паутины, известное миру, находится в Американском музее естествознания в Нью-Йорке. Для изготовления этого трехметрового произведения искусства потребовалось более 1 миллиона пауков и труд 70 рабочих. Более коротким путем пошли ученые из Университета Вайоминга. Благодаря генетической модификации коз удалось получить молоко, в котором присутствуют те же молекулярные структуры, что и в паучьем шелке.

В июне 2015 года стало известно о еще одном новом прорыве. Стартап Bolt Threads путем сбраживания дрожжей создал микроорганизмы, способные вырабатывать в большом количестве протеины, входящие в основу паучьего шелка. Полученную субстанцию ученые пропускают через сложную механическую систему, которая сжимает ее, превращая в твердые волокна. Уже в 2016 году в компании обещают выход технологии на рынок, а значит, очередная хорошая новость уже не за горами.

Изображения © gizmodo.com, blog.arkive.org, news.rice.edu, geo.ru, npr.org, arquitecturacarbono.wordpress.com

http://archspeech.com/article/chetyre-materiala-budushhego-ot-nanotrubok-do-pautiny

 

Эстетическое совершенство создаваемых форм во многом зависит от соответствия реальных стратегий их осмотра независимым наблюдателем априорным (непроверенным) стратегиям, стратегиям на которые ориентировался автор композиций. При этом под стратегией понимается проявление определенной устойчивой тенденции (регулярности) при выборе способов оценки изображений и принятия решений.    Проектирование композиций должно опираться на изученные  объективные стратегии зрительного восприятия (см. таб. 10).

 

Таблица.10. Стратегии зрительного восприятия.

Стратегия 1	уровневое восприятие
Стратегия 2	считывание изображения в направлении «слева - направо» и «сверху - вниз». Эта стратегия формируется к одиннадцати годам жизни человека. При этом необходимо указать на то, что стратегия считывания «слева – направо» является главной, более значимой. Стратегия «сверху – вниз» - менее значима.
Стратегия 3	объединение элементов композиций в визуальные группы по их признакам
Стратегия 4	переключение внимания наблюдателя от элементов с большей визуальной массой к элементам с меньшей визуальной массой.
Стратегия 5	движение глаз наблюдателя детерминируется (определяется) динамическими осями
Стратегия 6	фиксирование внимания наблюдателя в информативных точках контура и композиционных центрах: информативные точки (точки изменения направления линии контура), лежащие на выпуклых участках контура – являются главными, а на вогнутых участках – второстепенными.
Стратегия 7	наиболее быстрое и наиболее точное движение глаз по горизонтальным и вертикальным динамическим осям. Значимость динамических осей убывает в следующей последовательности: горизонтальная ось, вертикальная ось, все прочие оси.
Стратегия 8	уменьшение различительной способности около границы элемента и фона. Чем больше контраст, тем в большей степени имеет место понижение различительной чувствительности.

 

Процесс управляемого формально – композиционного построения формы должен начинаться по стратегии от общего к частному, т.е. с самого высокого уровня выделяемых элементов, соответствующего наибольшей абсолютной мерности будущего пространства, массы. Так, разработка интерьера начинается с построения композиции уровня «D» (как правило, соответствует мерности интерьерного пространства) в последовательности действий по таб. 11.

 

 

Таблица11.

1	Выбор состава ГЭ (геометрических элементов) композиции уровня «D» (1м-10м)
2.	строятся композиции визуальных групп выбранного уровня
3.	оценка эстетического совершенства композиций визуальных групп по критериям гармонической оптимальности (в случае низкого качества, делается возврат к первому этапу)
4.	организация общей композиции уровня «D»
5.	оценка эстетического совершенства общей композиции уровня по критериям гармонической оптимальности (при неудовлетворительном результате делается возврат к четвертому этапу)
6.	выбор окончательного варианта состава и структуры композиции уровня «D»
7.	переход к разработке формы на уровне «C», затем на уровне «B» и т.д.

 

При этом выполняются следующие действия: 2 и 5. Все части организуемой композиции должны объединяться определенной системой эстетически оправданных соотношений признаков. Для достижения этой цели необходимо использовать арифметические, геометрические и гармонические пропорциональные отношения числовых значений признаков, как наиболее подходящие для достижения визуальной связности (соразмерности) элементов. Выбирая количественные значения признаков и осуществляя их оптимизацию, следует использовать общие меры – модули, с которыми должны соотноситься величины признаков.

Так как зрительная система не способна одновременно отчетливо воспринимать элементы, относящиеся к центральным областям различных уровней (стратегия 1), задача оптимального структурирования внешнего вида объектов существенно упрощается. Разработчик вправе выбрать для различных уровней не связанные, каким либо образом значения модулей, с которыми должны соотноситься величины признаков. Важно указать и на то, что значения линейных модулей и координируемых с их помощью параметров должны быть одного порядка. Например, для координации линейных параметров элементов, габариты которых находятся в пределах 1 – 10 мм, не может быть выбрано значение модуля меньше одного миллиметра или более десяти миллиметров.

Основное правило модульной координации можно сформулировать следующим образом: параметры элементов, составляющих уровень, должны быть кратными выбранным для этого уровня линейному, угловому и цветовому модулям.

Допускается использовать различные (не кратные друг другу) модули для следующих действий:

· координации линейных параметров элементов уровня, если эти элементы расположены в различных плоскостях, сориентированы в разных направлениях, имеют различную форму и цвет;

· координации коэффициентов отражения поверхностей элементов, лежащих в различных плоскостях, сориентированных в различных направлениях, разной формы и размеров;

· координации угловых параметров элементов, если эти элементы расположены в различных плоскостях, имеют различную форму, разные размеры и цвет.

Организуя композиции уровней предметно-пространственной среды, а также визуальных групп внутри уровней архитектор должен добиваться визуально воспринимаемой целостности, упорядоченности и соподчиненности элементов. Необходимо помнить, что именно от этих сложных формальных свойств во многом зависит первое слагаемое эстетической оценки – красота.

Формальная целостность композиций достигается следующими приемами:

1. Соединением, пересечением или наложением друг на друга контуров визуальных групп, а в ряде случаев, контуров элементов;

2.  Введением дополнительных охватывающих элементов;

3. Сокращением разнообразия признаков до их оптимального количества.

Формальная упорядоченность обеспечивается путем размещения композиционных центров второстепенных элементов на динамических осях главных по отношению к ним элементов. Кроме того, путем построения композиций таким образом, чтобы участки контура, а также динамические оси ее главного и второстепенных элементов совпадали, были параллельны, перпендикулярны или располагались по определенному ясно прочитываемому закону.

Формальная соподчиненность достигается выбором в качестве главных, элементов с максимальной визуальной массой и размещением главных по функции элементов в ключевых точках композиции.

В ряде случаев, в качестве главного по смыслу элемента выступает элемент с относительно небольшой визуальной массой.

В архитектурно-проектной деятельности немаловажное значение имеет формальное единство элементов композиции. Единство элементов композиции достигается путем пересечения множеств признаков элементов визуальных групп, множеств признаков элементов различных визуальных уровней. В качестве общего признака, присущего всем элементам, подавляющему числу элементов или лишь главным элементам визуальных групп, как правило, выбирается идентичность геометрического вида формы (характер построения контура). В особо сложных композициях для достижения визуально воспринимаемого единства названный выше прием, основанный на использовании одного признака, оказывается малоэффективным. В таких случаях композиция строится на подобии контуров элементов, т.е. на равенстве как первичных, так и вторичных признаков.

Наряду с этим, необходимо следить за тем, чтобы в композициях визуальных групп не было встречных ритмов, а признаки элементов изменялись в соответствии с алгоритмом функциональной деятельности человека. Визуальное «сложение» различных по функциональному назначению элементов необходимо достигать путем нюансного отношения их признаков. Контраст признаков следует использовать как средство разделения элементов на визуальные группы.

 

 

Таблица 12.

методика	совокупность методов осуществления чего-либо
метод	представляется способом или их объединением и является составной частью методики
способ	совокупность приемов определяет тот или иной метод деятельности
прием	действие или совокупность действий
действие	проявление какой-либо силы, приводящей энергии

 

Рассмотренные ранее методы формально-композиционного формообразования, характеризующиеся как метод синтезации, трансформации и комбинированный метод в виде совокупности предыдущих, базируются на использовании свойственных им способах построения формы объектов.

Для метода синтезации определяющим и единственным способом является способ «сложение». Он представляет собой объединение в единую органичную систему энергетических потоков «поля» (или пространства)  композиции, образованных формами элементов, кластеров и контуров самой композиции. В результате возрастает визуально воспринимаемая целостность организуемой формы, усиливается ее общий энергетический потенциал. Как в физике, так и в теории композиции понятие «поле» является философским допущением, а именно названием вида материи, с которой связана действующая группа сил.

Рис.59.  Башня IFC , Хефей, Китай	Рис. 60. Боско Вертикаль, Милан, арх. Стефано Боери.
соприкосновение	группировка

 

Для способа «сложение» характерны приемы:

Наложения,

Вложения,

Охватывания,

5. сближения (группировки).

Реальное использование каждого приема предопределяется в зависимости от условий и задач по организации формы воображением автора, мысленной визуализацией будущей формы, наброском на бумаге. Условия организации формы, при этом, выступают как определенные, устанавливаемые автором или заказчиком правила по достижению задуманного эстетического и практического результата. В данном случае полезно не только представлять результат или эскизировать, но и вербализировать замысел и результат, составить его словесное описание в виде соотношений конкретных признаков и свойств будущей формы. Чаще всего, концепция формальной структурно-композиционной организации будущей формы является предметом предустановки, хотя результат творческого поиска может иметь отчасти эвристической происхождение.

Прием «соприкосновение» предполагает наличие контакта (касания) одних элементов формы другими. Границы (зоны) касания являются при этом общими частями элементов формы. Соприкосновение n – го количества элементов осуществляется через посредство точечного, линейного и поверхностного контакта. Сами элементы могут быть как одномерными, так и разномерными. Частный случай контактного объединения элементов - их блокировка как совокупность однотипных элементов.

Прием «наложение» определяет положение сверху одного элемента формы на другой. Уложение одного элемента формы на другой может быть полным (тождество), почти полным (нюанс) и частичным (контраст). В случае полного наложения тождественных элементов, новая форма отличается от исходных форм только геометрическими параметрами. Ее динамичность однонаправлена по вертикали. В других случаях динамичность форм может быть направлена раздельно как по вертикали, так и по горизонтали или совместно в обоих направлениях. При наложении элементов возникают зоны наложения, которые могут иметь точечный, линейный, поверхностный или комбинированный характер.

Прием «вложение» характеризуется размещением одного элемента формы в другом элементе. Следует подразделять вложение на скрытое и открытое. Скрытое вложение осуществляется по принципу «матрешка» и его результат визуализируется только при определенной «прозрачности» наружного элемента. Для открытого вложения, выполняемого по принципу «клетка», характерна прямая визуализация результата выполняемого действия. Прием вложения в реальной действительности, возможно, осуществить только совместно с приемом соприкосновения в силу воздействия гравитационных сил. Наиболее просто и наглядно данный прием можно визуализировать при использовании контуров разной степени сложности при выполнении матрицы вложений. Вкладываемые контуры, при этом, выступают как прямолинейные (Пк), криволинейные (Кк), ломаные (Лк) и комбинированные: ПКк, ПЛк, КЛк, и ПКЛк. Базовые контуры, определяющие строки матрицы, определяются, при этом, точно также, в последовательности сверху вниз. Межконтурная зона здесь может восприниматься как новая форма-масса. Возможно построение по данной матрице совокупностей вкладывающихся поверхностей, объемов и их комбинаций.

 

Рис. 61. Использование приемов «вложение», «охватывание» в специфическом решении оконных проемов.

 

Прием «охватывание» предопределяет заключение одного элемента в пределы другого элемента. Данный прием имеет много общего с приемом вложения и является как бы его частным случаем.

Рис. 62а. Арх. Бюро Аткинс, Бахрейн, деловой центр Шарк, 2007. Приемы контактной группировки (блокировки) геометрически сходных, но не одинаковых элементов, и «вложения» полученной группы геометрических элементов в контур.

Рис. 62б. Башни Этихад, Абу Даби, 305.3 м, 79 этажей, DBI Design's. Прием «охватывания», «вложения» бесконтактная группировка создают образ группы парусов, раковин, дополненный использованием первичных формально-композиционных признаков – текстуры, света и цвета серебристого и голубого архитектурного стекла и геометрического вида - криволинейных поверхностей и контуров.

 

В силу этого многие положения приема вложения могут быть транслированы на прием охватывания. Здесь выделяются охватывающий и охватываемый элемент (совокупность элементов). Также возможно построение матриц охватывания элементов.

Прием «сближение» являет собой группировку (объединение) элементов с расположением их близко, на малых расстояниях друг от друга. Это есть проявление, так называемого, бесконтактного синтеза с соотнесением элементов относительно друг друга или какого- то другого «мнимого» элемента, при этом действия не должны сводиться к простым механическим манипуляциям. Необходимо помнить, что любое сближение, путем изменения расстояний между объектами, усиливает в голове наблюдателя желание сравнить, сопоставить соседствующие объекты. При сближении человеку свойственно улавливать все большее количество признаков, и если среди них нет равенства, то все отчетливее ощущается отторжение, а не ожидаемое нами соединение объектов. Следовательно, сближаемые объекты должны иметь определенный набор качественно одинаковых признаков. Малый объект, попадая в область «поля» большего объекта, начинает как бы «пропитываться» его признаками. Чем дальше от центральной области композиции находится элемент, тем больше свободы в его решении получает проектировщик, тем более самостоятельным может быть пластическое решение удаленного элемента.

Кластер как явление, возникающее в результате синтезации, т.е. сближения признаков и расположения некоторого множества объектов, стал в настоящее время и термином теории систем и наименованием некоторой типологически однородной совокупности планировочных единиц, которые в теории формальной композиции могут рассматриваться как плоскостные, поверхностные структурно-композиционные образования.  Понятие «кластер» происходит от англ. cluster — скопление, кисть, рой) — объединение нескольких однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определёнными свойствами. Кластер в градостроительстве — территориальное образование внутри мегаполиса, представляющее собой относительно автономную единицу и обеспечивающее своим жителям полный набор городских функций (жилую, административно-деловую, торгово-развлекательную, рекреационную).

Вышеперечисленные приемы способа сложения обеспечиваются совокупностью правил такого построения новых форм. Эти правила учитываются в момент создания концепции, предустановки при определении использования того или иного приема и предполагают получение в результате более органичной формы объекта (таб.13.).

Таблица 13.

п/п	ФОРМУЛИРОВКА ПРАВИЛА
1.	· сокращение разнообразия признаков элементов и кластеров
2.	· соединение динамических осей элементов в общем композиционном центре
3.	· размещение второстепенных элементов на динамических осях главных по отношению к ним элементов;
4.	· расположение элементов на объединяющем их общем элементе
5.	· выбор симметричного или ассиметричного расположения элементов
6.	· назначение абсолютно одинаковых элементов в качестве главных элементов складываемых кластеров или композиций
7.	· выбор абсолютно одинаковых элементов в качестве ключей образуемых кластеров или композиций
8.	· неприменение встречных векторов динамичности
9.	· усиление целостности композиций уровня Ј (обозначение произвольного уровня), состоящей из двух и более обособленных кластеров, путем создания целостных кластеров из элементов уровня Ј – 1
10.	· усиление целостности композиции путем обеспечения равенства или пересечения множеств значений признаков элементов или кластеров

Использование в процессе предустановки всех этих правил не под силу человеку, возможно лишь при использовании дигитальных средств моделирования высокой мощности. Множество данных правил может выступать в качестве приемов трансформации при организации форм согласно комбинированному методу формально-композиционного формообразования.

 

Лекция 7.

Таблица14. Методы трансформации.

МЕТОД ТРАНСФОРМАЦИИ	ПРИНЦИПЫ	1. транспозиции, заключающийся в перестановке заданных элементов формы;
		2. модификации, представляющий собой видоизменение, преобразование исходных элементов формы, характеризующееся появлением новых признаков (свойств);
		3. модуляции, выступает как размеренное, закономерное изменение какого-нибудь признака формы без получения новых свойств;
		4. деструкции, предполагающий разрушение (нарушение) структуры формы;
		5. трансляции, состоящий в переносе на определенное расстояние элемента формы или их совокупностей;
		6. фрактальности, заключающийся в закономерной генерации самоподобных элементов являющихся исходными формами.

Envelope House Project Devercity Arhitects Иллюстрации вставить

В рамках метода трансформации организация оптимальной структуры формы осуществляется использованием способов «вычитания», «умножения», «деления», «акцентирования».

Способ «вычитание» представляет собой разъединение энергетических потоков, образованных геометрическими формами элементов композиции на самостоятельные подсистемы. В результате усиливается значимость, появляющихся при этом, новых ключей народившихся кластеров, также их главных элементов.

«Вычитание» достигается, как правило, действиями обратными сложению, но есть среди них приемы, на которые необходимо обратить особое внимание.

Рис. 64а. SHIBAURA HOUSE Architect: Kazuyo Sejima , Tokyo, Japan, 2011: способ вычитания, прием «перфорирования» за счет ограждающих конструкций с разной степенью прозрачности.	Рис. 64б. Тот же прием, использованный З. Хадид, с удалением фрагментов формы, башня Восхода Солнца (Sunrise Tower: «вертикальный лендморфный объект). Включает жилые, офисные, торговые, гостиничные помещения, паркинг. Куала Лумпур, Малазия. 2009 – TBC Sunrise Berhad Competition http://www.zaha-hadid.com/architecture/sunrise-tower/
Способ «вычитание».	Способ «вычитание».

 

ОСНОВЫ ТЕОРИИ АРХИТЕКТУРНОГО ФОРМООБРАЗОВАНИЯ

 

Учебно-методическое пособие

по подготовке к лекциям

 

 

для студентов ННГАСУ, обучающихся по дисциплине

 «Основы теории архитектурного формообразования»

по направлению подготовки 07.03.01 Архитектура,

профиль: Архитектурное проектирование

 

 

Нижний Новгород

ННГАСУ

2016

УДК 72. 011

 

Голов Г.М. Основы теории архитектурного формообразования: учебно-метод. пос. /Голов Г.М., Чеберева О.Н.; Нижегор. гос. архитектур.- строит. ун-т – Н.Новгород: ННГАСУ, 2016. - –157 с.– 1 электрон. опт. диск (CD-R).

 

 Учебно-методическое пособие для подготовки к лекциям построено в соответствии с авторской методикой Геннадия Михайловича Голова (1948-2015) с акцентом на формальном структурно-композиционном морфогенезе на основе формально-композиционной комбинаторики первоэлементов: точки, линии, контура, поверхности (плоскости), объема. Содержание процесса структурно-композиционного построения архитектурной формы раскрыто, как художественно-композиционная деятельность архитектора в соединении с математическими подходами к моделированию пространственных структур. Рассмотрены стратегии зрительного восприятия архитектурной формы, иерархия формально-композиционных простых и сложных признаков формы, основополагающие формально-композиционные свойства формы – первичные (простые) и вторичные (сложные комплексные), смоделированы алгоритмы неоптимизированного и оптимизированного формообразования. Определяется понятие геометрической модели формы (ГМФ), геометрического элемента (ГЭ) формы, вводится аналитический интеллектуальный инструмент формальной структурно-композиционной комбинаторики ГЭ формы (матрица - морфер). На основе аналогий природоподобия введены методы синтезации и трансформации, определяющие основную массу способов и приемов комбинаторно-геометрического построения формы. Раскрыты формально-композиционные и геометрические основы моделирования архитектурной формы, особенностей ее анализа и синтеза. Освещена типология и вопросы организации точечных, линейных, поверхностных (поверхностно-линейных, топологических) и объемных структур.

 

Предназначено для обучающихся в ННГАСУ по дисциплине «Основы теории архитектурного формообразования», направлению подготовки 07.03.01 Архитектура,

Профиль: Архитектурное проектирование

Учебно-методическое пособие ориентировано на обучение в соответствии с календарным учебным графиком и учебным планом ННГАСУ по основной профессиональной образовательной программе направления 07.03.01 Архитектура, профиль: Архитектурное проектирование

 

 

© ННГАСУ, 2016

©Г. М. Голов, О.Н. Чеберева, 2016

 

 

СОДЕРЖАНИЕ:

 

I.	Раздел 1: Архитектурно-исторический	5
	Лекция 1. 1.1 Введение. Исторический аспект художественно-композиционных закономерностей в архитектуре и других видах искусства. 1.2.   Проблема формы в древнерусском зодчестве.	5
	Лекция 2.  2.1. Структура архитектурной формы и её формально-композиционные свойства: 2.2. Базовые положения процесса неоптимизированного формообразования.	19
	Лекция 3. 3.1.Оптимизированное формообразование и его композиционные характеристики    3.2. Формально-композиционные первичные признаки формы.	32
	Лекция 4. 4.1. Формально-композиционные вторичные признаки формы. 4.2.Простые формально-композиционные свойства формы (средства гармонической оптимизации).	54
	Лекция 5. 5.1. Сложные формально-композиционные свойства формы (критерии гармонической оптимальности). 5.2. Формально-композиционный анализ признаков и свойств формы.	64
II	Раздел 2. Теоретический.	74
	Лекция 6. 6.1. Базовые принципы формально-композиционного формообразования.         6.2.Приемы формально-композиционной синтезации (интеграции) формообразующих элементов.	74
	Лекция 7. 7.1. Приемы формально-композиционной трансформации формообразующих элементов. 7.2. Геометрические закономерности формально-композиционного формообразования	83
	Лекция 8. 8.1. Особенности построения точечных формально-композиционных структур. 8.2. Особенности построения линейных формально-композиционных структур.	114
	Лекция 9. 9.1. Особенности построения поверхностных формально-композиционных структур. 9.2. Особенности построения объемных формально-композиционных структур.	133
	Библиография	155

                                                                                       

 

Раздел I. Архитектурно-исторический.

 

Эти правила, язык знаков и грамматика Игры, представляют собой некую разновидность высокоразвитого тайного языка, в котором участвуют самые разные науки и искусства, но прежде всего математика и музыка (или музыковедение), и который способен выразить и соотнести содержание и выводы чуть ли не всех наук. Игра в бисер – это, таким образом, игра со всем содержанием и всеми ценностями нашей культуры, она играет ими примерно так, как во времена расцвета искусств живописец играл красками своей палитры. Всем опытом, всеми высокими мыслями и произведениями искусства, рожденными человечеством в его творческие эпохи, всем, что последующие периоды ученого созерцания свели к понятиям и сделали интеллектуальным достоянием, всей этой огромной массой духовных ценностей умелец Игры играет как органист на органе, и совершенство этого органа трудно себе представить – его клавиши и педали охватывают весь духовный космос, его регистры почти бесчисленны, теоретически игрой на этом инструменте можно воспроизвести все духовное содержание мира.

Лауреат нобелевской премии

Г. Гессе, « Игра в бисер»

 

Лекция 1. Проблема формы древнерусском зодчестве.