Под деформированной задачей будем понимать задачу, в которой вместо числовых данных или ключевых слов стоят «окошки». В «окошки» нужно вставить недостающие числовые данные либо слова и решить полученную задачу.
Например:
1. Сын c отца на 25 лет. Сколько лет сыну, если отцу 45 лет?
2. В вазе стояло c белых роз и 14 красных. Сколько всего роз в вазе?
3. Мише надо решить 15 примеров. Он уже решил c примеров. Сколько примеров ему осталось решить?
Использовать деформированные задачи можно с различными целями: как подготовительную работу к чему-либо (введению составных задач и др.), для иллюстрации и закрепления свойств арифметических действий, как самостоятельный объект изучения, как творческую работу над задачей и т.д.
Работа над деформированными задачами содержит в себе большие возможности для учителя. П.М. Эрдниев и Б.П. Эрдниев отмечают, что «где выполняется деформированное упражнение, там срабатывает механизм обратной связи, а там, где есть непрерывная подсознательная коррекция и исправление ошибок, там и достигается прочность знаний» [22, с. 94].
Анализ условия деформированной задачи позволяет детям наиболее полно осмысливать связи в задачах, определение границ числа, которое можно подставить в «окошечко» или аргументация выбора соответствующего слова заставляет детей представлять реальную ситуацию, моделью которой является задача.
Рассмотрим функции деформированных задач.
Деформированные задачи можно использовать в качестве подготовительных для введения составных задач (М.И. Моро):
1. В одном цехе 10 станков, а в другом на 4 станка меньше. Сколько станков во втором цехе?
2. В одном цехе 10 станков, а в другом c станков. Сколько станков в двух цехах?
После решения первой задачи, учитель предлагает детям прочитать вторую задачу. Дети замечают, что вторую задачу решить нельзя, так как нет конкретного числа станков во втором цехе. Тогда учитель предлагает ответ первой задачи использовать в условии второй задачи вместо «окошечка». Дети формулируют новую задачу и решают ее.
При помощи деформированных задач также осуществляется функциональная пропедевтика в начальной школе (М.В. Богданович, М.И. Моро). Например: «На грядке росло 12 тюльпанов. Для букета срезали c тюльпанов. Сколько тюльпанов осталось на грядке?» (СНОСКА: [Б1, С.64.])
При работе над этой задачей дети должны подобрать числа, которые можно подставить в «окошко» (пропедевтика понятия переменной величины), а также определить границы данного числа (пропедевтика понятия области допустимых значений переменной). Через урок вводится понятие переменной (буквы) в выражении.
Однако, далее деформированные задачи в учебниках почти не встречаются, хотя их можно использовать как один из приемов насыщения урока задачами, а также в творческой работе над задачей.
На примере конкретной задачи рассмотрим методические проблемы и возможности, возникающие при деформации задач. Дано задание: «На одном тракторе работали в течение недели 60 ч, а на другом – 55 ч. На втором тракторе при одинаковой норме расхода за неделю израсходовали горючего на c, чем на первом. Сколько литров горючего израсходовали на каждом тракторе за неделю? Текст задачи испорчен, надо восстановить и решить задачу. Как вы думаете, какие данные в тексте испорчены?» В данной задаче пропущено не только число, но и отношение «меньше на». Пытаясь восстановить текст задачи, дети активно и самостоятельно анализируют ее содержание. Для того, чтобы подобрать нужные данные, они должны понять, о чем идет речь в задаче, установить смысловые, причинно-следственные связи, догадаться о наличии конкретной связи и проверить правильность предположения. Анализ содержания задачи становится активным и более быстрым, так как сознание детей направлено не на сам анализ, а на восстановление текста. Это значит, что большая часть работы по анализу содержания задачи проходит в блочных, свернутых формах (законы УДЕ). Для того, чтобы восстановить текст, ребенок должен рассуждать и делать выводы. Дети догадались, что пропущено число и слово. Но какое слово? Раз написано «на», то это слово либо «больше», либо «меньше». И тут самые догадливые понимают, что не может быть слова «больше», только «меньше». Почему? Потому, что второй трактор работал меньше времени, значит и горючего израсходовал меньше. А разве это правильное рассуждение? Ну и что, что он работал 55 часов, а не 60 часов. Ведь может у него такой мощный мотор, что он за это время горючего больше потратил. И дети должны заметить, что норма расхода горючего у обоих тракторов одинакова. Значит, действительно, второй трактор потратил горючего меньше. Нужное слово найдено «меньше». Что полезного в проделанной работе? Дети рассуждали, спорили, отстаивали свою правоту. Значит шел активный анализ связей в задаче. Дети выделили прямо пропорциональную зависимость между временем работы и расходом горючего при постоянной норме расхода горючего.
Теперь надо подобрать число. На сколько литров горючего меньше мог израсходовать за неделю второй трактор? Возникает проблема: для того, чтобы подобрать число, нужно иметь жизненный опыт, нужно хотя бы примерно знать нормы расхода горючего в неделю. Если дети подбирают большие числа, можно рассказать о цене литра горючего для трактора, что, допустим, если недельные расходы каждого трактора отличаются на 1000 л, то это очень дорого и т.д. Мальчишки, обычно, интересуются техникой, и могут знать приблизительно недельную норму расхода горючего для трактора. Если знатоком по нормам расхода окажется ученик, которого до этого в классе не замечали, то его заметят, а он, в свою очередь, поймет, что задачи – это интересно. Если никто так и не подберет числа, – предлагайте сами. Итак, дети предлагают числа, и решают задачи, которые получились. Можно использовать такие варианты краткой записи:
Таблицей
| Норма расхода | Время | Расход горючего | |
| I | ? | 60 ч | ? |
| Одинаковая | |||
| II | ? | 55 ч | ?, на … л меньше |
Отрезками

Дальше дети видят, что разница в расходе горючего приходится на 5 часов работы трактора, значит, для того, чтобы задача решалась, нужно подобрать число, которое делится на 5. В результате в неявном виде повторяется таблица деления на 5, подбираются внетабличные случаи деления на 5, таким образом, решается целая серия примеров. Если записывать решение задач выражением, то при различных данных будет получена серия задач и выражений к ним:
| 35 л | 35: (60–55)× 60=420 (л) | 420–35=385 (л) |
| 30 л | 30: (60–55)× 60=360 (л) | 360–30=330 (л) |
| 25 л | 35: (60–55)× 60=300 (л) | 300–25=275 (л) и т.д. |
Таким образом, решена не одна задача, а целая серия задач, на которую потрачено меньше времени, чем при решении каждой задачи отдельно на другом уроке.
Теперь можно предложить детям пронаблюдать, как изменялись ответы при изменении данного, предложить подобрать данные так, чтобы оба ответа увеличились (40 л.), чтобы оба ответа уменьшились (20 л) и т.д. таки образом проводится функциональная пропедевтика.
А если ребенок предложил число 28 л? Нужно объяснить детям, что задача будет решаться, но только числа будут дробными.
| 28 л | 28: (60–55)× 60=… (л) | …–28=… (л) и т.д. |
Например: «Если бы мы умели выполнять действия с дробями, то получили бы ответы 336 л и 308 л. Действия с дробями будут изучаться позже, но если кому-то интересно как они выполняются уже сейчас, пусть подойдут ко мне после уроков». Так вы заинтересовываете детей математикой и проводите опережающее обучение.
Деформированные задачи можно использовать в организации устного счета, в организации парной, групповой работы. Дети с удовольствием решают задачи, составленные их товарищами. При этом составляющий задачу должен подумать, будет ли данная задача решаться, т.е. еще и еще раз проанализировать связи в задаче.
Подведем некоторые итоги работы над данной конкретной деформированной задачей:
1. Деформация позволила сделать активным анализ содержания задачи.
2. Анализ связей в задаче также активен и происходит в неявных формах.
3. Осуществляется связь с практикой, с жизнью, опора на личный опыт.
4. Возникают возможности уплотнения материала, укрупнения дидактических единиц обучения, так как возникает серия примеров задач, решенных за короткое время.
5. Идет активное развитие мыслительных операций: сравнение, анализ, синтез и т.д.
6. Открываются возможности повторения материала на качественно новом уровне, а также пропедевтической работы к изучению математики в старших классах.
7. Обобщается способ решения задачи.
8. Детям интересно работать.
Рассмотрим другие возможные варианты методики работы над деформированными задачами.
Пусть дана задача: «У мальчика 5 серых кроликов и 4 черных. Сколько кроликов у мальчика?» (СНОСКА: [Б1, С.33]) Эта задача рассматривается при изучении табличного сложения и вычитания 4 без перехода через десяток. На доске записываем краткую запись:

Решение: 5+4=9 (к.)
После решения задачи можно провести следующую работу.
Видоизменить краткую запись всеми возможными способами:
1)
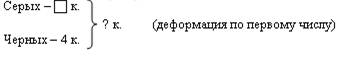
2)
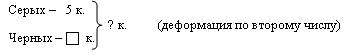
3)
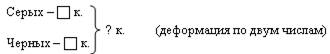
Первый вид деформации позволяет тут же закрепить только что составленную таблицу прибавления 4. (Какой ответ получится, если серых кроликов 1, 2, 3, 4? Ни одного?) При подстановке других чисел, если дети еще не умеют их складывать, можно использовать предметные действия. Деформация по второму числу позволяет повторить табличное сложение с 1,2, 3. Деформация по двум числам дает возможность вспомнить все возможные случаи табличного сложения (и не только), известные детям.
Если задачу такого вида рассмотреть после изучения табличного сложения, то можно работать с серией задач при фиксированном первом или втором слагаемом, еще раз пронаблюдать свойство монотонности суммы.
В задаче «Сын c отца на 25 лет. Сколько лет сыну, если отцу 45 лет?» детям вместо «окошка» (или многоточия) поставить подходящее слово. Для того чтобы выбрать требуемое слово (моложе), ребенок должен проанализировать условие задачи и жизненную ситуацию, о которой идет речь в задаче.
В случае, когда в задаче предлагается заменить ключевые слова, появляется возможность работать не только с разными числовыми данными, но и с разными видами задач.
Например: «Из одного пункта выехали две машины в противоположном направлении. Скорость одной машины 60 км/ч. Скорость второй – 80 км/ч. Какое расстояние будет между ними через 2 часа?»
Если эту задачу деформировать так: «Из одного пункта выехали две машины в c направлении. Скорость одной машины 60 км/ч. Скорость второй – 80 км/ч. Какое расстояние будет между ними через 2 часа?», появляется возможность решить две задачи (движение в одном и различных направлениях).
Если деформировать задачу так «Из одного пункта выехали две машины в противоположном направлении. Скорость одной машины 60 км/ч. Скорость второй – 80 км/ч. Какое расстояние будет между ними через c часа?», то будет возможность решить каскад задач.
Деформированные задачи можно рассматривать как частный случай задач обобщенного вида (вместо частных числовых данных вводятся символы переменных – «окошки», буквы или другие символы). Их можно использовать для проверки сформированности у учащихся умения решать задачи данного вида.
Например, рассмотрим деформированную задачу (фигурами Ñ, ∆, c обозначены числа): «На тарелке лежало c груш и Ñ яблок. Сколько фруктов осталось на тарелке, если с нее взяли ∆ фруктов?».
Задания по данной задаче могут быть такими:
1. Составьте выражение-схему для решения задачи, используя символы задачи.
2. Подставьте вместо символов числа, решите задачу. Какими должны быть числа Ñ, ∆, c, чтобы задачу можно было решить только одним способом, двумя способами, тремя способами? И т.д.
Данное задание покажет, сформированы ли у детей навык решения задач данного вида, а также обобщенные знания о свойствах действий. Чтобы выполнить данные задания, учащиеся должны будут рассуждать, что способствует формированию логического мышления.
Рассмотрим применение деформированных задач при работе над обратными задачами.
Дана краткая запись задачи и несколько кратких записей задач, среди которых есть задачи, обратные данной. Например, прямая задача может выглядеть так:

Задание можно сформулировать так: «По приведенным кратким записям выбери задачи, обратные данной, если ее ответ обозначен ∆». Обратными данной будут те задачи, в которых вместо одного из данных символов исходной задачи будет стоять знак вопроса, а вместо искомого исходной задачи стоит ее ответ. Далее можно предложить еще задание: «Можно ли среди данных задач выбрать взаимообратные между собой задачи? Ответ объясни» и т.д.
Даны числа D,Ñ, ÿ. Числа D,Ñ входят в условие задачи, ÿ – искомое число. Чем будут являться эти числа для задач, обратных к данной задаче? (К любой простой задаче можно составить две обратные. В одной из них искомым будет число D, данными будут числа Ñ, ÿ. В другой искомое число Ñ, данные числа D, ÿ).
Задача решается так: D–Ñ=ÿ. Как будут решаться обратные задачи? (В задаче данными являются числа D,Ñ, а искомым числом ÿ. Для обратных задач записи решений будут такими: D–ÿ=Ñ и Ñ+ÿ=D).
Выполнение приведенных упражнений поможет выявить уровень сформированности у учащихся понятия «обратная задача», а также умения выбирать действия по решению простых задач и обосновать свой выбор.
Упражнения
1. Рассмотрите деформированную задачу: «Брат c (старше, моложе) сестры c (в, на) c лет. Сколько лет сестре, если брату c лет?» Составьте различные задачи на основе этой. Какие трудности могут возникнуть в процессе работы над такой задачей?
2. Найдите в учебниках [Б1], [Б2], [Б3], [М1], [М2], [М3] деформированные задачи (если они есть). Проанализируйте цели их применения.
3. Дана задача: «В швейной мастерской было 90 м шелка. Когда сшили несколько платьев, расходуя по 3 м на каждое, то осталось еще 60 м. Сколько платьев сшили?» (СНОСКА: [Б2, С.171]) Деформируйте задачу различными способами. Продумайте, как организовать работу с детьми над этой задачей.
Дата: 2018-12-28, просмотров: 716.