Необходимое условие решения сложной задачи – умение решать простые задачи, к которым сводится любая составная задача. При наличии такого умения вся проблема состоит в том, чтобы найти ту совокупность простых задач, решение которых приведет к выполнению требования основной задачи. Здесь возможны два основных пути поиска решения: синтетический и аналитический (по Н.В. Метельскому).

Часто при решении составной задачи многие ученики берут любое данное из условия задачи и к нему присоединяют какое-либо из остальных данных. Если эти данные образуют простую задачу, то ее решают, если простой задачи не получилось, образуют другую пару данных и в результате решения первой простой задачи получают первое вспомогательное данное. Используя вспомогательное данное и какое-либо из остальных данных основной задачи, решают вторую простую задачу и получают второе вспомогательное данное и т. д., до тех пор, пока не получат такой простой задачи, результат которой является искомым основной задачи.

Это и есть синтетический метод решения задач. Если основную задачу условно записать: АÞX, а первую и последнюю из конечной совокупности простых задач, из которых состоит решение основной задачи, обозначить соответственно через а1 и аn, то процесс решения задачи синтетическим методом можно записать в виде:

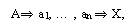
Синтетический метод широко применяется при решении задач арифметическим способом.

Основной недостаток синтетического метода – отсутствие какого бы то ни было критерия в вопросе, с чего, с каких данных начинать решение и какие вспомогательные величины определять, какие простые задачи решать в дальнейшем, чтобы решить основную задачу. Этот метод мало пригоден для отыскания новых решений и слабо способствует научению школьников самостоятельно решать задачи, логически рассуждать, продуктивно мыслить. Пользуясь синтетическим методом, учащиеся нередко выполняют лишнюю работу, а иногда слабый ученик может предложить бессмысленное действие. Единственное, на что в некоторой степени можно опереться, применяя синтетический метод – это прошлый опыт ученика в решении задач, аналогии, ассоциации, которые может вызвать решаемая задача. Некоторую помощь учащимся оказывает здесь и анализ, проявляющийся в скрытой, неявной форме.

Достоинством синтетического метода является компактность, достигаемая при изложении готовых решений, полученных в процессе синтетического или аналитического поиска.

Несмотря на низкую поисковую и дидактическую эффективность синтетического метода, он пользуется популярностью у школьников и даже учителей, поскольку весьма прост и не требует большого мыслительного напряжения.

При аналитическом методе решения отправляются не от условия задачи, как это делают при синтетическом методе, а от ее требования, вопроса. Это характерно для всех разновидностей аналитического метода, применяемых при решении задач.

Решение задач аналитическим методом начинается с постановки следующего вопроса, связанного с требованием решаемой задачи: «Что нужно знать, чтобы ответить на вопрос данной задачи (выполнить ее требование)?» Для правильного ответа на поставленный вопрос необходимо знать данные задачи и учитывать те зависимости, которые связывают их с искомым числом.

Пусть для вычисления искомого Х основной задачи требуется знать, например, числа pi и qi, из которых при помощи некоторого математического действия можно получить X, т. е. решить основную задачу. Таким образом, сначала основная задача с требованием Х преобразовалась в первую серию вспомогательных задач с искомыми pi и qi, Обозначим первую серию вспомогательных задач через В1. Ставим тот же вопрос к каждой из вспомогательных задач: «Что нужно знать, чтобы найти p1 (q1), и опять при ответе на этот вопрос используем условие (А) основной задачи, а также взаимосвязи между этими данными.

Пусть для вычисления p1 требуется знать p2 и q2, а для вычисления q1, — знать p2’ и q2’. Теперь основная задача преобразовалась во вторую серию (B2) вспомогательных задач, включающую задачи по нахождению p2 и q2, p2’ и q2’,

Продолжая процесс преобразования, получаем, наконец, такую серию (Вn) вспомогательных задач, искомые которых содержатся во множестве данных основной задачи. Искомое число любой из вспомогательных задач предыдущих серий также могло оказаться известным, и тогда эта вспомогательная задача не подвергается преобразованию с помощью аналитического метода.

Таким образом, основная задача решена аналитическим методом, поскольку этим методом проведен поиск и найден путь решения задачи, главное здесь именно в этом, а не в оформлении записи уже известного решения.

Найденное аналитическое решение можно изложить различными способами, в том числе и синтетическим. В последнем случае пришлось бы следовать от конца аналитического рассуждения к его началу, не производя при этом никаких поисков.

Если основную задачу условно записать формулой АÞX, описанный выше аналитический путь преобразования задачи изобразится схемой: а первую и последнюю из конечной совокупности простых задач, из Х –В1 –В2 – … – Вn-1 – Bn, где АÞ Bn, BnÞВn-1, …, В1ÞX

Если после внимательного ознакомления ученика с условием и требованием задачи путь решения ему очевиден или почти очевиден, поиск решения лучше осуществлять синтетическим методом. Аналитический метод применяется тогда, когда задача достаточно сложная и прошлый опыт ученика не подсказывает ему плана решения или примерного направления поиска.

В практике решения задач методы анализа и синтеза полностью разделить, изолировать друг от друга невозможно. Они полезно сочетаются. При аналитическом методе имеют место скрытые элементы синтеза. Например, преобразуя требование основной задачи в требования первой серии вспомогательных задач, мы неявно проверяем правильность этого преобразования, возможность синтезирования из искомых чисел задач первой серии искомого основной задачи.

Хотя путь поиска на основе аналитического метода решения не всегда однозначен, однако он все же менее многозначен и более определенен, чем путь поиска при синтетическом методе решения. Аналитический метод удобен для поиска пути решения новой для учащихся задачи, он опирается на определенное умение школьника рассуждать и эффективно способствует развитию его продуктивного, логического и функционального мышления. В результате систематического применения аналитического метода решения у учащихся быстрее формируется умение самостоятельно решать новые для него задачи, чем при пользовании синтетическим методом. Аналитический метод решения задач на вычисление должен найти достаточно широкое применение и рациональное сочетание с другими методами.