На основе аналитического и синтетического методов решения задач при работе над поиском решения задачи применяются два основных способа разбора задачи: аналитический (анализ) и синтетический (синтез). Однако на практике чаще употребляют аналитическо-синтетический разбор задачи.

Под анализом подразумевают способ рассуждений от общего к частному (анализировать – разбивать на составляющие), таким образом при разборе текста задачи от вопроса к данным применяется аналитический способ.

Под синтезом подразумевают способ рассуждений от частного к общему (синтезировать – получать из частей). В задачах это разбор от данных к вопросу, однако, назвать этот метод чисто синтетическим нельзя, т.к. прежде, чем получать метод разбора от данных к вопросу, эти данные нужно предварительно вычленить из задачи, т.е. проанализировать условие задачи.

Непосредственно сам разбор задачи представляет собой цепочку рассуждений, основанных на анализе и синтезе. Организуя разбор задачи вместе с детьми, учитель должен продумать систему специально подобранных вопросов, при помощи которых организуется выбор решения задачи. Эти вопросы не должны быть наводящими, должны вести к самостоятельному выбору решения. Разбор составной задачи заканчивается составлением плана решения. Если вы разбираете задачу с одновременным составлением схемы разбора, то план решения прослеживается прямо по схеме.

Проиллюстрируем различные способы разбора задач на примере следующей задачи: «За день туристы преодолели 100 км. 84 км они проехали автобусом, а остальной путь прошли пешком за 4 часа. Сколько километров туристы проходили за 1 час?» [Б3, №716].

В результате анализа содержания задачи появляется ее краткая запись в виде чертежа:

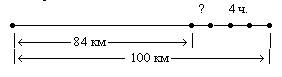
Направление рассуждений будет следующим:

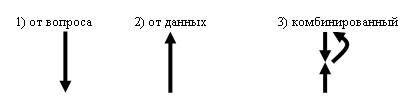
1) Разбор от вопроса к данным.

Что спрашивается в задаче? (Сколько км туристы проходили за 1 час?) Что нужно знать, чтобы ответить на этот вопрос? (Путь, который прошли туристы и время, которое они затратили на этот путь). Можно ли сразу узнать, сколько км туристы проходили за 1 час? (Нельзя, т.к. мы не знаем путь, который они прошли). Можно ли сразу узнать путь, пройденный пешком? (Можно). Почему вы думаете, что можно? (Так как мы знаем общий путь и путь, пройденный пешком). Далее осуществляется наметка плана решения.

Схема разбора задачи появляется одновременно с самим разбором.

2) Разбор от данных к вопросу.

Выберите два данных в задаче, по которым можно сразу что-то узнать. (100 км и 84 км). Что можно узнать по этим данным? (Путь, пройденный туристами пешком). Предположим, что мы узнали этот путь. Что сказано об этом пути в задаче? (Что он пройден за 4 часа). Что можно было бы узнать, если известен путь и известно время его прохождения? (Скорость движения на этом участке пути). Где это можно использовать в решении задачи? (Ответим на вопрос задачи). Что можно узнать? (Скорость движения туристов пешком).

Далее следует наметка плана решения.

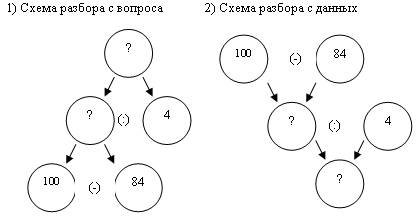
3) Комбинированный разбор.

Что спрашивается в задаче? (Сколько километров туристы проходили за 1 час?). Можно ли сразу узнать скорость? (Нет). Почему нельзя? (Не известен путь, пройденный пешком). В задаче еще есть два числа, какие? (Весь путь 100 км и путь, проделанный на автобусе 84 км). Что можно узнать по этим данным? (Путь, пройденный туристами пешком). Нам это пригодится? (Да, мы сможем найти путь, пройденный пешком).

Далее следует наметка плана решения.

Рассмотрим типичные ошибки, которые допускают студенты, а зачастую и учителя начальных классов при разборе задач. Например: вернемся к задаче «С первого участка было собрано 5 одинаковых корзин моркови, а со второго – три такие же корзины, причем с первого участка собрали на 30 кг моркови больше, чем с первого. Сколько килограммов моркови собрали с каждого участка?».

а) от вопроса к данным: Каков главный вопрос к задаче? (Сколько килограммов моркови собрали с каждого участка?) Можем ли мы сразу на него ответить? (Нет). Почему? (Не знаем массу одной корзины). Как же найти массу одной корзины? (Нужно знать массу нескольких корзин и их количество). Почему морковь, собранная с первого участка весила на 30 кг больше? (Т.к. с этого участка собрали больше корзин). Можно ли узнать, какое количество корзин весит 30 кг? Каким действием? (Вычитанием). Можно ли теперь ответить на главный вопрос задачи? (Да. Можем найти массу одной корзины, а также знаем количество корзин). Каким образом? (Сначала делением найдем массу одной корзины, потом умножением массу пяти и трех корзин).

) от данных к вопросу (чаще всего используется учителями начальной школы): Зная, сколько корзин собрали с 1-го и 2-го участков, что можно найти? (На сколько корзин больше собрали). Каким действием? (Вычитанием). Теперь, зная, на сколько корзин больше собрали с 1-го участка, чем со 2-го и на сколько килограммов больше, что можно найти? (Массу одной корзины). Каким действием? (Делением). Зная массу 1 корзины и количество корзин, что можно найти? (Общие массы моркови). Каким действием? (Умножением).

Второй способ разбора (б) данной задачи не дает детям возможности выбора другого способа решения, кроме предложенного учителем. Получается, что учитель навязывает ученикам способ решения задачи, лишая их возможности думать и действовать самостоятельно. Первый способ разбора (а) наиболее полно выделяет основные связи в задаче, однако тоже содержит подсказку решения.

Рассмотрим еще один способ разбора данной задачи.

б1) от данных к вопросу (отличается от способа (б) тем, что не навязывает детям способа решения, а помогает выбрать из всех возможных связей те, которые нужны для решения данной задачи). Какой главный вопрос задачи? (Сколько моркови собрали с каждого участка?) Что значит «с каждого участка»? (Это значит с первого участка и со второго участка). Можем ли мы сразу ответить, сколько моркови собрали с первого участка? (Нет). А со второго участка? (Нет). Почему? (У нас недостаточно данных). Какие данные у нас есть? (Количество корзин, собранных с первого участка и со второго участка, а также, на сколько килограммов моркови больше собрали с первого участка). Зная, сколько корзин собрали с 1-го и 2-го участков, что можно найти? (Сколько корзин собрали всего, с какого участка собрали больше (меньше) корзин и на сколько). Какими действиями? (Сложением или вычитанием). Подумайте, что мы можем узнать, если будем знать, сколько корзин всего. (Мы могли бы узнать, сколько килограммов моркови в одной корзине, но для этого мы не знаем общую массу всех корзин. Или сколько килограммов моркови всего, но для этого мы не знаем массу одной корзины. Следовательно, эти данные нельзя будет использовать). А сможем ли мы использовать при решении знание того, на сколько больше (меньше) корзин собрали с одного из участков? (Да. Если мы будем знать, на сколько корзин больше собрали с первого участка и на сколько больше килограммов собрали с этого участка, мы сможем сделать вывод, что именно на эти корзины и приходятся 30 кг, данные в задаче). Значит, зная, на сколько корзин больше собрали с одного из участков и сколько килограммов приходится на эти корзины, что можем найти? (Какова масса одной корзины). Каким действием? (Делением общей массы корзин на их количество). Теперь, если мы знаем массу одной корзины и количество корзин, собранных с каждого из участков в отдельности, что можно найти? (Можно найти массу моркови, собранную с каждого из участков в отдельности и общую массу всей моркови с двух участков). Какой из вариантов нужен нам, что бы ответить на вопрос задачи? (Сколько килограммов моркови собрали с каждого участка в отдельности. Найдем действием умножения).

Многочисленные психологические исследования показали, что анализ выступает в различных формах: анализ-«фильтр» и анализ через синтез. При применении анализа-«фильтра» человек, решающий задачу просто наугад ищет ее решение, пробуя все возможные варианты, отбрасывая ненужные. Анализ через синтез представляет собой основу любого мыслительного процесса, поэтому его использование при решении задач предпочтительнее.

Упражнения

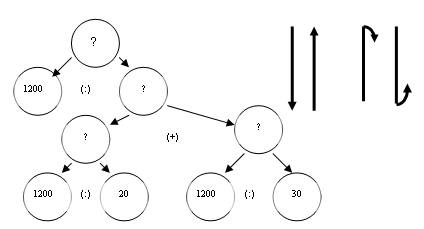
1. Дана задача: «Из двух городов, расстояние между которыми 1200 км, вышли одновременно навстречу друг другу два поезда. Один из них проходит это расстояние за 20 часов, другой за 30 часов. Через сколько часов поезда встретятся?» Рассмотрите схему разбора этой задачи и подумайте ее разбор с вопроса; с данных; комбинированным способом. Какой способ разбора кажется вам наиболее удачным? Как вы думаете, от чего зависит выбор способа разбора задачи?

2. Дана задача: «В один магазин привезли 15 ящиков с фруктами, в другой 10 таких же ящиков. В первый магазин привезли фруктов на 60 кг больше, чем во второй. Сколько килограммов фруктов привезли во второй магазин?» Сделайте разбор задачи разными способами с использованием схемы разбора. Выберите наиболее удачный способ ее разбора. Дополните разбор графической иллюстрацией.

3. К задаче из предыдущего задания приготовьте серию вопросов, предназначенных для: запоминания чисел; отделения известного от неизвестного; выделения величин и установления связей между ними; разбиения задачи на смысловые ситуации; прогнозирование ответа. Синтезируйте все подготовленные вопросы в краткую беседу. Можно сопровождать ее иллюстрацией. Что дает такого рода работа над задачей?