Запись арифметического решения задачи может быть выполнена по-разному:
1. по действиям с ответом;
2. по действиям с пояснениями после каждого действия;
3. с вопросами перед каждым действием;
4. по действиям с предварительной записью плана;
5. числовым выражением;
6. схематической моделью;
7. комбинированным способом, включающим в себя несколько вышеперечисленных.
Проиллюстрируем возможные способы записи арифметического решения задач на примере задачи о корзинах с морковью. Напомним ее содержание: «С первого участка было собрано 5 одинаковых корзин моркови, а со второго – три такие же корзины, причем с первого участка собрали на 30 кг моркови больше, чем с первого. Сколько килограммов моркови собрали с каждого участка?»
Запись решения по действиям с ответом
1. 5–3 = 2 (к.)
2. 30:2 = 15 (кг)
3. 15×5 = 75 (кг)
4. 15×3 = 45 (кг)
Ответ: с первого участка собрали 75 кг моркови, а со второго – 45 кг.
Запись решения по действиям с пояснениями после каждого действия
1. 5–3 = 2 (к.) – больше с первого участка;
2. 30:2 = 15 (кг) – масса одной корзины;
3. 15×5 = 75 (кг) – собрали с первого участка;
4. 15×3 = 45 (кг) – собрали со второго участка.
Ответ: с первого участка собрали 75 кг моркови, а со второго – 45 кг.
Запись решения задачи с вопросом к каждому действию
1. На сколько корзин больше собрали с первого участка?
5–3 = 2 (к.)
2. Какова масса одной корзины?
30:2 = 15 (кг)
3. Сколько килограммов моркови собрали с первого участка?
15×5 = 75 (кг)
4. Сколько килограммов моркови собрали со второго участка?
15×3 = 45 (кг)
Ответ: с первого участка собрали 75 кг моркови, а со второго – 45 кг.
Запись решения задачи с планом решения
1. Узнать, на сколько корзин больше на 1 участке (вычитание).
2. Узнать массу 1 корзины (деление).
3. Узнать массу моркови, собранной с первого участка (умножение).
4. Узнать массу моркови, собранной со второго участка (умножение).
1) 5–3 = 2 (к.)
2) 30:2 = 15 (кг)
3) 15×5 = 75 (кг)
4) 15×3 = 45 (кг)
Ответ: с первого участка собрали 75 кг моркови, а со второго – 45 кг.
Запись решения задачи при помощи числового выражения
Данная задача в записи решения будет иметь не одно, а два числовых выражения. Это связано с тем, что в задаче практически два вопроса, на каждый из которых нужно ответить.
1. 30:(5–3)×5=75 (кг)
2. 30:(5–3)×3=45 (кг)
Ответ: с первого участка собрали 75 кг моркови, а со второго – 45 кг.
Выбор формы записи решения зависит от ситуации на уроке и навыков письма детей. Например, если дети пишут медленно, на уроке можно ограничиться записью решения задачи по действиям с ответом или выражением, а на дом задать задачу и потребовать описать её. Запись решения задачи выражением более компактна и показывает, что ребенок понимает все связи в задаче.
Как показывает практика, многие студенты педагогических факультетов, а иногда и учителя начальных классов не понимают разницы между различными способами решения и различными формами записи решения задачи. Один и тот же способ решения текстовой задачи можно записать каждым из первых пяти перечисленных выше форм.
Рассмотрим возможные варианты обучения детей записи решения задачи при помощи числового выражения.
На этапе ознакомления с решением задач нового типа этот способ записи решения задачи могут использовать не все учащиеся, а лишь единицы. На данном этапе целесообразно использовать запись решения задачи по действиям с вопросами или пояснениями, либо в соответствии с составленным планом.
Если же навык решения задач данного вида отработан, то запись решения числовым выражением имеет ряд преимуществ: учащемуся требуется гораздо меньше времени на оформление задачи; появляется возможность решить за урок гораздо больше задач. Ведь не секрет, что младшие школьники пишут медленно, а запись решения задачи выражением более компактна. Кроме того, решая задачи составлением выражений, дети лучше готовятся к обучению в старших классах. Углубляются знания свойств и законов арифметических действий, представления о числовом выражении и его значении, т.е. осуществляется алгебраическая пропедевтика. В задачах с буквенными данными решение записывается только выражением.
Анализ методической литературы по вопросу обучения детей записи решения задачи составлением выражения и анализ просмотренных уроков математики в начальной школе позволил нам выделить следующие подходы к решению данного вопроса: способ последующей работы над записью решения задачи и способ поэтапной записи выражения в процессе решения задачи (названия автора).
Приведем примеры организации учебно-познавательной деятельности учащихся при их обучении записи решения задач при помощи числового выражения двумя вышеперечисленными способами.
Первый способ – способ последующей работы над записью решения задачи выражением после ее решения по действиям. Работа над решением задачи и его записью проводится в такой последовательности: учащиеся сначала решают задачу по действиям, а потом учитель предлагает составить по полученным действиям выражение.
Пусть дана задача: «В 5 одинаковых коробок можно положить 30 кг печенья. Сколько потребуется таких коробок, чтобы упаковать 54 кг печенья?»
Решение:
1) 30:5=6 (кг) – масса одной коробки.
2) 54:6=9 (к.)
Ответ: потребуется 9 коробок.
Выражение: 54:(30:5)=9 (к.)
Если учитель объясняет, как составлено это выражение, то это часто выглядит так:
Рассмотрим последнее действие – 54:6. Число 54 дано в условии, а числа 6 в условии нет. Как было получено число 6? (30:5).
Заменим число 6 выражением 30:5. Мы должны показать, что это первое действие, поэтому нужно поставить скобки. Получилось выражение 54:(30:5).
Итак, выражение составляют, начиная с последнего действия и следя за тем, чтобы в нем остались только те числа, которые даны в условии задачи.
Второй способ – способ поэтапной записи выражения. Детей учат записывать выражение к задаче, делая это постепенно, с пояснениями.
На примере это может выглядеть так:
Что узнаем сначала? (Массу одной коробки с печеньем).
Как? (30:5).
Запишем это выражение, но вычислять его значения не будем.
30:5 (кг) – масса коробки с печеньем.
Что узнаем потом? (Сколько понадобится таких коробок для 54 кг печенья).
Как? (54 разделим на выражение, полученное в первом действии, т.е. на массу одной коробки: 54:(30:5) (к.)).
Мы составили к задаче выражение, теперь найдем его значение.
Многие учащиеся в этом случае говорят, что если бы сразу нашли ответ первого действия, то задача была бы уже решена. Такая запись заставляет дважды рассматривать решение задачи. Потеря времени не нравится детям, многие уже нашли ответ по действиям и не видят смысла другой записи решения задачи.
Оба эти способа обучения записи решения задачи выражением являются традиционными.
Мы предлагаем третий способ обучения записи решения задачи составлением числового выражения – способ одновременного анализа задачи и составления выражения к ней. При этом можно одновременно научить детей делать схему разбора задачи, используя ее вместо краткой записи.
Разбор при этом начинают с вопроса:
Что спрашивается в задаче? (Сколько потребуется коробок для упаковки 54 кг печенья?)
Какие два данных нам нужно знать для ответа на этот вопрос? (Надо знать, сколько было печенья и сколько его помещается в одну коробку).
Есть у нас эти данные? (Массу печенья знаем, а массу одной коробки не знаем, знаем только, что она одинакова).
А если бы знали массу одной коробки, то каким действием нашли бы ответ? (Делением).
Запишем это.
Появляется запись (рис.1).
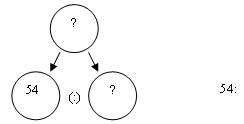
Рис.1
А можно ли узнать массу одной коробки? (Можно).
Почему вы так думаете? (Все коробки одинаковые, знаем, что 30 кг упаковали в 5 коробок).
Каким действием узнаем массу одной коробки? (Делением).
Получилось выражение (рис.2).
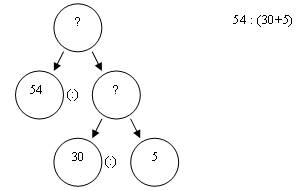
Рис.2
Найдем его значение, надписав промежуточный результат сверху. Запишем ответ. Окончательно запись выглядит так (рис.3).
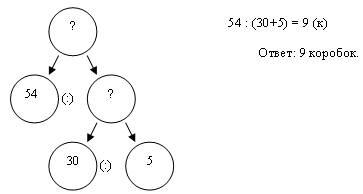
Рис.3
Покажем такую же работу на примере более сложной задачи. Дана задача «Один трактор работал в неделю 50 ч, а другой – 48 ч. Оба трактора при одинаковой норме израсходовали 686 л горючего. Сколько литров горючего израсходовал за неделю каждый трактор?»
Окончательная запись в тетради при решении этой задачи в тетради имеет вид (рис.4).
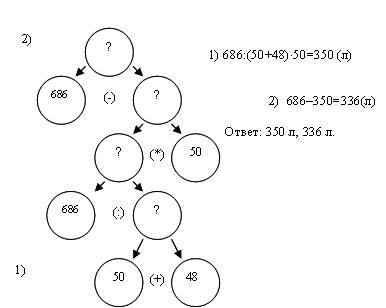
Рис.4
Эта запись возникает постепенно, в процессе анализа задачи учеником.
Рассмотрим ее появление блоками:
Что означают слова «каждый трактор»? (Это значит первый и второй трактор в отдельности). Какие данные у нас есть, чтобы узнать расход горючего первым трактором? (Время работы знаем, а расход горючего в час не знаем). Если бы знали, то каким действием нашли бы ответ? (Умножением). Запишем это (рис.5).
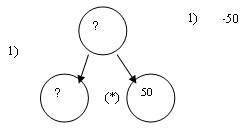
Рис.5
Надо узнать расход горючего в час. Что для этого надо знать? (Общий расход горючего – 686 л и время, за которое это горючее израсходовано. Это время мы не знаем).
Каким действием мы могли бы узнать расход горючего в час, если бы знали время? (Делением).
Запись принимает вид (рис.6).
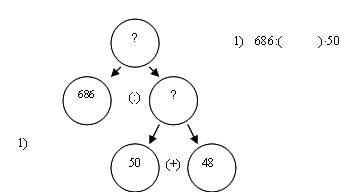
Рис.6
Можно ли узнать это время? (Можно. Есть оба данных: 50 ч и 48 ч.). Каким действием? (Сложением).
Запись принимает вид (рис.7).
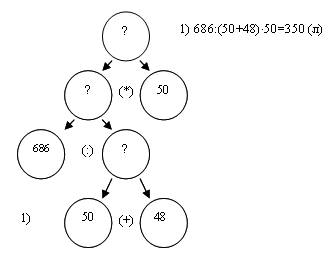
Рис.7
1) 686:(50+48)×50=350 (л)
1)
Что осталось узнать? (Сколько горючего израсходовал второй трактор).
Можно это узнать? (Можно).
Почему? (Всего израсходовали 686 л, и первый трактор израсходовал 350 л, значит, остальное горючее израсходовал второй трактор). Запись приобретает вид (рис.4).
Возможен и другой способ нахождения ответа на последний вопрос, он нас тоже устроит. Появляется окончательная запись решения. Письменно дети подсчитывают только то, что не могут сосчитать устно. Наличие схемы разбора в тетради не обязательно, ее можно делать на черновике. Учитель может проконтролировать понимание решения различными способами, как прямыми, так и косвенными (прямые – объяснить устно каждый шаг, написать план решения и т.д.; косвенные – решить похожую задачу, составить обратную и т.д.).
Предложенный способ позволяет экономить время записи решения задач. Кроме того, в процессе данной работы дети овладевают деятельностью схематизации, а затем и моделирования (анализ текста задачи, математизация, преобразование модели, соотнесение полученной модели с задачей). Именно такая деятельность помогает детям глубже проникнуть в суть задачи. При одновременном построении схемы разбора задачи и записи решения виден развернутый план решения задачи и арифметические действия, которые необходимо выполнить. Схема разбора выступает в данной ситуации в двух функциях: абстрактной модели и конкретного отображения содержания, связей и решения задачи.
Выбор приема ознакомления детей с записью решения задачи составлением числового выражения, на наш взгляд, должен осуществляться дифференцированно, в зависимости от состава класса. Можно применять все три приема последовательно. Например, сначала объяснить материал третьим способом, затем, по необходимости, применять первый и второй способы в индивидуальной работе.
Некоторые учителя записи решения задачи числовым выражением предпочитают запись решения по действиям, мотивируя тем, что ребенок должен пояснять каждое действие, и это является гарантией того, что он понимает решение задачи. Но ведь если ребенок записал выражение для решения задачи, то им уже прослежены все связи, он понимает, как решена задача.
Часто методические объединения учителей математики школы второй ступени считают, что запись задачи по действиям с вопросами или пояснениями является пропедевтикой решения задач алгебраическим способом, и поэтому настоятельно рекомендуют учителям начальной школы требовать от детей оформлять запись решения задачи только по действиям с вопросами.
На наш взгляд, в пропедевтику решения задач при помощи уравнения входят две равноправные части:
1. запись задачи по действиям (с пояснениями или вопросами), что является подготовкой непосредственного описания решения задачи;
2. запись решения задачи при помощи выражения, что является подготовкой к составлению и записи самого уравнения.
Ведь чтобы составить уравнение к решению задачи учащийся должен не только проанализировать и описать каждую связь между искомым и данными задачи, но и связать их в единое целое – уравнение. Практически те же навыки и требуются от ребенка при оформлении записи решения задачи выражением в школе первой ступени: проанализировать задачу, выявить все связи между искомым и данными, записать выражение.
Проверка решения задачи
Программа по математике для начальных классов ориентирует на обязательное овладение всеми учащимися различными способами проверки решения задач. Работа по формированию навыков контроля и самоконтроля при решении задач очень важна. Ведь проверка решенной задачи позволяет не только убедиться в правильности решения, но и способствует более глубокому пониманию и осмыслению ее математического содержания, осознанию связей между величинами, представленными в задаче. Однако, как правило, при проверке решения задачи активное участие принимают лишь некоторые ученики, ведущие объяснение. Остальные же занимают позицию пассивных слушателей, или исполнителей, даже если задача была решена ими неправильно.
Обучение проверке решения задач представляет собой полноценный этап в обучении детей решению задач. Оно должно быть специально организовано, проводиться целенаправленно и систематически. Причем на первых этапах обучения решению задач, когда у детей еще не достаточно сформированы навыки контроля и самоконтроля, имеет смысл предлагать учащимся после решения задачи проверить, правильно ли она решена.
Приведем примеры заданий, которые необходимо предлагать учащимся для того, чтобы выработать у них внутреннюю потребность проверять решение задач:
1. При решении задачи обязательно объясните себе, почему решаете так, а не иначе.
2. После решения задачи прочитайте снова текст задачи и проверьте, все ли требования задачи выполнены, правильно ли.
3. Составьте план решения задачи. Какой пункт в решении задачи будет последним? (Работа над задачей заканчивается проверкой ее решения).
Учителю необходимо побуждать учащихся проверять выполнение любого упражнения, задачи в том числе.
Существуют следующие способы проверки решения задачи:
1. анализ ответа и прикидка ответа;
2. решение задачи другим способом;
3. подстановка результата в условие (установление соответствия между числами из условия и результатом);
4. составление и решение обратных задач;
5. сверка результата с ответом, данным в конце учебника (в начальной школе – сообщенным учителем).
Некоторые методисты относят графический способ решения задачи к отдельному способу проверки. На наш взгляд, этот способ относится к решению задачи другим способом.
Ожидаемый ответ задачи должен быть проанализирован, например, при ответе на вопрос «Сколько квартир на этаже?» явно не должно быть числа (–159) или 5,7 квартиры.
Прикидка обычно проводится перед решением задачи, устанавливаются границы значений искомого числа. После получения ответа проверяют, удовлетворяет ли он выбранным границам. В случае несоответствия делают вывод о неправильности результата.
Применять этот способ можно как для простых, так и для составных задач. Данный способ является необходимой частью анализа задач в косвенной форме, в связи с тем, что еще до решения задачи нужно выяснить, какое число получится в ответе – больше или меньше данного. Проиллюстрируем применение этого способа проверки конкретными примерами.
1) «Торт стоит 20 грн., а коробка конфет 8 грн. На сколько гривень коробка конфет дешевле торта?».
Прочитайте задачу. Что в задаче известно? (Цена торта 20 грн., цена коробки конфет 8 грн.). Значит, в ответе задачи должно получиться число, меньшее 20 на 8. Выполняя решение задачи, дети получат
20 – 8 = 12 (грн.), что подтверждает правильность предыдущих рассуждений.
2) «Сыну 8 лет, что на 25 лет меньше, чем отцу. Сколько лет отцу?».
Прочитайте задачу. Подумайте, какое число должно получиться в результате? Больше или меньше, чем 8? (Больше, так как отец старше сына). На сколько больше? (На 25).
3) «В одном бидоне осталось 4 литра молока, а во втором – 6 литров. Сколько литров молока осталось в двух бидонах?»
Данная задача относится к разряду задач, трудных для восприятия детьми, поскольку они привыкли, что слово «осталось» связано с действием вычитания. Для предупреждения ошибки в решении необходимо использовать прикидку. Дети должны прийти к выводу, что в результате должно получиться число, большее, чем каждое из чисел условия.
4) «В одном ящике 5 кг помидоров, а в другом 8 кг таких же помидоров. Сколько нужно заплатить за каждый ящик, если вся покупка стоит 26 грн.?»
Какова стоимость каждого ящика? Больше или меньше стоимости всей покупки? (В результате должно получиться два числа, меньших, чем 26). Какой ящик стоит дороже? (Второй). Почему? (Так как в нем больше помидоров). После выполнения решения задачи, получаем, что первый ящик стоит 10 грн., а второй – 16 грн. (10<16).
Однако стоит отметить, что данный способ проверки целесообразно применять не для всех задач.
Решение задачи другим способом можно применять лишь в том случае, если таковой существует. При совпадении результатов в обоих способах решения делается вывод о его правильности.
Например:
Из двух сёл, расстояние между которыми 69 км, навстречу друг другу выехали два велосипедиста. Через какое время они встретятся, если скорость одного 11 км/ч, а другого – 12км/ч.
Решение:
1 способ:
1) Какова скорость сближения?
11 км/ч + 12 км/ч = 23 км/ч
2) Через сколько часов они встретятся?
69 км : 23 км/ч = 3 ч.
Ответ: велосипедисты встретятся через 3 часа.
2 способ:
Пусть х часов – время движения до встречи. Тогда один из велосипедистов до встречи проехал 11х (км), а второй – 12х (км). Учитывая общее расстояние, пройденное ими, составим уравнение:
11х + 12х = 69
23х = 69
х = 3 (ч).
Ответ: велосипедисты встретятся через 3 часа.
Вывод: при различных способах решения получены одинаковые ответы, следовательно, задача решена верно.
Проверим решение этой задачи подстановкой. Действительно, если оба велосипедиста находились в пути до встречи 3 часа, то:
11·3 = 33 (км) – прошел первый до встречи;
12·3 = 36 (км) – прошел второй;
33+36 = 69 (км) они прошли вместе.
Вывод: задача решена верно.
Составление и решение обратных задач – один из интереснейших способов проверки задачи. Традиционная методика рекомендует вводить его лишь во втором классе, однако, работая в системе укрупнения дидактических единиц, составлять и решать обратные задачи начинают в первом классе при изучении обратных действий сложения и вычитания [18]. При этом дети наиболее полно понимают связи между величинами и наблюдают обратные по отношению друг к другу действия. Часто обратная задача бывает сложнее прямой. Работа над обратными задачами не будет сложной, если начать её как можно раньше. Дети всегда с удовольствием составляют и решают задачи, обратные данной.
Обратной задачей к данной является та, которая содержит искомое число в качестве известного, а какое-либо из известных чисел прямой задачи становится неизвестным.
Например, эти задачи являются обратными:
1. Из двух сёл, расстояние между которыми 69 км навстречу друг другу выехали два велосипедиста. Через какое время они встретятся, если скорость одного 11 км/ч, а другого – 12км/ч.
2. Из двух сел навстречу друг другу выехали одновременно два велосипедиста и встретились через 3 часа. Каково расстояние между селами, если их скорости 11 км/ч и 12 км/ч соответственно.
К данной задаче можно составить ещё 2 обратные задачи, где искомыми будут являться скорости велосипедистов. Составьте их и решите все задачи.
Рассмотрим традиционную методику работы над обратными задачами. Многие методисты отмечают проявление некоторого формального отношения к использованию этого приема работы.
В учебнике математики для II класса предложено несколько заданий, требующих составления обратных задач. Этот вид упражнений является полезным и эффективным средством при овладении учащимися умением решать арифметические задачи. В процессе этой работы учащиеся осмысливают и углубляют знания связей между различными величинами, например: «цена – количество – стоимость» или «расход чего-либо на единицу – количество единиц – общий расход» и другими.
Составление обратных задач также рассматривается методистами как один из видов творческих упражнений, направленных на преобразование одной задачи в другую, на сравнение их условия, решении, ответов. Однако, М.В. Богданович отмечает, что «составление обратной задачи как способ проверки можно использовать для любой задачи, но он громоздкий и его следует применять, преследуя одновременно и другие цели работы над задачей» [3, с.47].
К сожалению, составление обратных задач учителя не всегда связывают с проверкой решения задач. Причина может быть не только в громоздкости, но и в невладении методикой данной работы. Это не позволяет учителю полностью использовать возможности обратных задач, либо ведет лишь к формальному выполнению проверки.
Для выполнения проверки решения прямой задачи способом составлением обратной задачи и ее решения, дети должны овладеть следующим алгоритмом:
1. решить исходную задачу;
2. подставить результат в текст исходной задачи в качестве известного данного;
3. обозначить новое неизвестное в задаче;
4. составить новую задачу по отношению к данной;
5. решить составленную задачу;
6. сравнить полученный результат с тем данным, которое сделали неизвестным;
7. сделать соответствующий вывод (если числовые значения совпадут, то задача решена верно).
Осознанное выполнение полного состава действий данного алгоритма является обязательным дидактическим условием. Проверка считается выполненной, если сделаны выводы на основе сравнения числа, полученного при решении обратной задачи с данным числом прямой задачи. Выполнение этого действия позволяет сделать вывод о правильности или неправильности решения задачи.
Рассмотрим фрагмент урока во втором классе по теме «Знакомство с обратными задачами».
К учебным целям урока относятся:
а) познакомить детей с понятиями «прямая задача», «обратная задача»;
б) раскрыть прием составления задачи, обратной данной;
в) показать, что составление обратной данной задачи и ее решение можно рассматривать как один из способов проверки решения задачи;
г) познакомить детей с алгоритмом проверки прямой задачи путем составления и решения обратной.
Ход урока:
Дети самостоятельно решают задачу: «Коробка конфет и торт вместе стоят 19 грн. Конфеты стоят 8 грн. Сколько стоит торт?»
Дети решают задачу, записывают решение
19 – 8 = 11 (грн.).
Далее работу можно организовать так: О чем решали задачу? (О конфетах и торте). На доске появляется иллюстрация задачи.
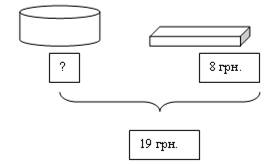
Что было известно в задаче? (За всю покупку уплатили 19 грн., а за конфеты 8 грн.). Что узнавали в задаче? (Сколько стоит торт. Он стоит 11 грн.). Все числовые значения учитель подписывает под рисунками на иллюстрации задачи. Как узнали цену торта? (От 19 грн. отняли 8 грн.). Почему выбрали действие вычитания? (19 грн. стоят торт и конфеты, следовательно, торт стоит меньше 19 грн. на 8 грн.).
Далее учитель закрывает запись общей стоимости покупки знаком вопроса, знак вопроса – записью цены торта. Что теперь известно в задаче? (Купили торт за 11 грн. и коробку конфет за 8 грн.). Что нужно узнать? (Сколько заплатили за всю покупку). Мы получили новую задачу. Сформулируйте условие задачи по этим данным. (Купили торт за 11 грн. и коробку конфет за 8 грн. Сколько стоит вся покупка?).
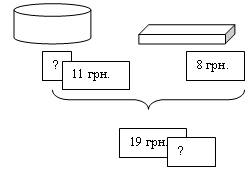
После анализа нового условия задачи дети ее решают и записывают решение в тетрадь.
11 + 8 = 19 (грн.).
Какой ответ получили? (Вся покупка стоит 19 грн.). Чему была равна стоимость всей покупки в первой задаче? (Тоже 19 грн.). Можем ли мы сказать, что при решении первой задачи цена торта найдена правильно? Почему вы так думаете? (В решении новой задачи получили 19 грн. – это стоимость всей покупки. В первой задаче дано было 19 грн. Значит, цену торта мы нашли правильно, потому, что 11 грн. и 8 грн. – это 19 грн.). Итак, мы проверили решение первой задачи.
Что мы для этого делали? (Составили новую задачу и ее решили). Подумайте, когда мы точно можем сказать, задача решена правильно. (Если мы составим и решим новую задачу и в ответе получим число, которое было дано в первой задаче, значит, первая задача решена правильно).
Запомните: исходная задача, которую мы решали первой называется прямой задачей, а новая задача, которую мы составили для проверки решения прямой задачи, называется обратной задачей. С помощью решения обратной задачи мы проверили решение данной задачи.
Что же мы делали, чтобы составить обратную задачу. (Число, которое было известным в условии задачи, мы сделали неизвестным, а неизвестное — известным).
Подумайте, можно ли еще составить задачу, обратную данной прямой задаче. (Можно, если принять за неизвестное цену коробки конфет).
Составьте вторую обратную задачу, решите ее и докажите, что решение обратной задачи позволяет проверить решение данной задачи.
Далее понятие обратной задачи и способа проверки с ее помощью закрепляется по учебнику.
В результате проделанной работы учащиеся должны усвоить, что для составления обратной задачи необходимо преобразовать предложенную задачу так, чтобы ее искомое стало известным числом, а одно из данных чисел стало искомым. Кроме этого, если при решении обратной задачи в результате получили число, которое было известное прямой задаче, то можно с уверенностью сказать, что предложенная задача была решена правильно.
При составлении обратных задач к задачам, в основе решения которых лежат знания конкретного смысла арифметических действий, учащиеся обычно не допускают ошибок. Однако часто ошибаются в составлении обратных задач к задачам, содержащих отношения «больше» и «меньше», заменяя не полученные числа, а само отношение. Это говорит о том, что у учащегося, который допускает такую ошибку, не сформировалось понятие «обратная задача».
Рассмотрим конкретный пример: учащиеся, составляя обратную задачу к задаче: «В одной коробке 15 карандашей, а в другой на 5 карандашей меньше. Сколько карандашей во второй коробке?», составили такую задачу: «В одной коробке 15 карандашей, а в другой на 5 карандашей больше. Сколько карандашей во второй коробке?». Причина ошибки может быть в том, что ученики, считая, что обратная задача должна решаться действием, обратным прямой, составляют задачу, которая решается действием сложения, которое обратно действию вычитания. Это показывает на формальное усвоение знаний этими учениками. Действительно, составленная учащимися задача решается действием сложения, являющимся обратным к действию вычитания. Однако, эту задачу нельзя рассматривать как обратную к исходной, так как при ее составлении было заменено отношение между данными, а не числовые значения и вопрос.
Для устранения этой типичной ошибки полезно использовать в сравнении краткие записи условий как прямой, так и обратных задач.
| Прямая задача | Обратные задачи | |
| I – 15 кар. II – ?, на 5 кар. меньше | I – 15 кар. II – 10 кар., на ? меньше | I – ? кар. II – 10 кар., на 5 меньше |
Схематическое изображение задачи позволяет учащимся пронаблюдать, что при составлении обратной задачи изменяются только числовые значения, отношения в задаче остаются неизменными.
С другой стороны, если бы обратная задача составлялась с целью проверки решения предложенной задачи, то учащиеся могли бы сами обнаружить свою ошибку. Ведь они при решении обратной задачи получили число, которое не соответствует ни одному из числовых значений прямой задачи.
Часто случается так: ученик решает задачу, а затем проверяет ее решение действием, обратным к выполненному, не составляя текст обратной задачи. Такая «проверка» не всегда позволяет убедиться в правильности решения прямой задачи, а проверяется лишь правильность вычисления, а не правильность выбора арифметического действия. Часто дети, у которых еще не сформирован конкретный смысл арифметических действий, вне зависимости от контекста задачи, решают задачи, в которых содержатся слова «улетели», «вышли в море», «съели», «уехали» и т.д. действием вычитания, хотя в задаче может спрашиваться сколько всего выехало, улетело, ушло и т.д. Рассмотрим конкретную задачу. «В море вышли 5 сейнеров и 4 катера. Сколько кораблей вышло в море?» Ученик, ориентируясь на слово «вышли» ассоциирующееся с процессом уменьшения, выбирает действие вычитания: 5–4=1. Составленное обратное действие (4+1) не позволяет ему выявить ошибочность выбора арифметического действия, так как работа идет в отрыве от математического содержания задачи. Ученик при решении получает в ответе числе 5 и успокаивается, хотя проверил лишь вычисление. А ведь в предложенной задаче необходимо было найти сумму двух слагаемых (все корабли – это сейнеры, их 5, и катера, их 4). Если бы ученик при проверке решения задачи составил условие обратной задачи, а не ограничился только составлением обратного действия, он получил бы следующее: «В море вышел 1 корабль. Из них 4 катера и несколько сейнеров. Сколько сейнеров вышло в море?» Полученное условие задачи противоречиво, поэтому можно было бы сделать вывод об ошибке в решении.
Чаще всего причина такого роди ошибок в том, что у учащегося не сформирован алгоритм проверки решения задачи. Раскрытие алгоритма проверки решения арифметических задач должно стать предметом специального рассмотрения, когда раскрывается содержание каждого действия, входящего в процесс проверки, обосновывается последовательность их выполнения, что приводит к пониманию и осознанию самого приема работы.
Как же можно организовать работу над обратными задачами с первого класса? Рассмотрим методику, предложенную П.М. Эрдниевым. В методике УДЕ применяются укрупненные задания, которые, как правило, состоят из выполнения трех последовательных пунктов:

При таком подходе к работе над обратными задачами (и в качестве способа проверки решения и в качестве творческой работы над задачей) учащиеся при составлении обратных задач не допускают ошибок, описанных ранее.
Рассмотрим конкретные примеры.
Дети рассматривают картинку, на которой мальчик с 5 марками в альбоме и девочка с 2 марками [18].
Учитель предлагает составить задачу по картинке.
«У мальчика было 5 марок, а у девочки 2 марки. Сколько марок у детей вместе?»
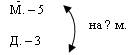
Учитель делит доску на три части вертикальными линиями (в задаче три числа, значит, кроме прямой задачи можно будет составить еще две обратных задачи). Дети делают то же самое в тетради. Квадратик неизвестного числа можно рисовать и ручкой и карандашом, после решения полученный результат заносить в этот квадратик. В верхней строке таблицы записывается так называемая «схема задачи» (термин П.М. Эрдниева), т.е. сначала по порядку записываются числа, которые даны в задаче, а затем ставится «окошечко» для записи неизвестного числа.

В первую колонку заносится решение первой задачи.
Учитель говорит, что решена прямая задача, но к данной прямой задаче можно составить две обратных. В первой задаче предлагается сделать неизвестным число 5. Запись приобретает вид:

Учитель предлагает составить задачу по данной схеме.
«У мальчика и девочки всего было 7 марок. Из них 2 марки было у девочки. Сколько марок было у мальчика?»
Учитель спрашивает, как решить задачу. Дети говорят, что от 7 марок отнять 2 марки останется 5 марок. Запись будет такая:
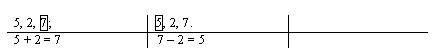
Аналогичная работа проводится по составлению и решению второй обратной задачи.
«У мальчика и девочки всего было 7 марок. Сколько марок было у девочки, если у мальчика было 5 марок?»
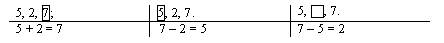
Окончательная запись в тетради учащегося будет такая:
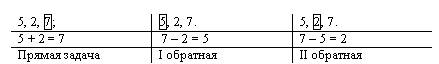
Дети записывают решения трех взаимообратных задач в трех колонках, вверху схема задачи, внизу – решение задачи.
И при введении задач обратных задач по методике УДЕ и по традиционной методике обратите внимание на трудности, которые возникают у учащихся при составлении текста обратных задач. Дети часто пытаются составить обратную задачу по аналогии с прямой задачей. Например: «Дети собирали марки. У мальчика было неизвестно сколько марок, а у девочки 2. А вместе марок у детей 7». Полученная формулировка, конечно, может быть использована. Однако детям стоит показывать различные образцы формулировок задач, убеждать в том, что текст задачи должен быть сформулирован таким образом, чтобы она была понятна всем, кто ее будет решать, чтобы задача была «красивой», «благозвучной», при этом четкой и без лишней информации (первая фраза в задаче «Дети собирали марки»).
Составление и решение обратных задач не только является интересным способом проверки решения задачи, но и творческой работой над задачей. Кроме того, решение обратных задач является одним из приемов насыщения урока задачами.
Если вам удобно работать над задачей с учащимися по другой краткой записи (дети привыкли использовать именно такую форму или другие причины):
Мальчик – 5 м.
Девочка – 2 м.
Всего – 7 м.,
то схему для работы по составлению обратных задач можно, на наш взгляд, записывать после решения прямой задачи, при этом, не заполняя вторую строчку предложенной таблицы. Запись задачи может выглядеть так:
Задача.
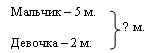
Решение:
1) 5 + 2 = 7 (м.)
Ответ: у детей 7 марок.
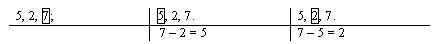
Если же в своей работе вы используете мобильные схемы, похожие на схемы С.Н. Лысенковой, то можно просто менять числа и знаки вопроса в соответствующих кармашках на демонстрационной схеме и на индивидуальных схемах у детей.
Прямая задача:
I обратная
II обратная
Упражнения
1. Какие способы решения использовались для решения данной задачи о шишках и желудях? Предложите еще несколько способов решения данной задачи. Какой способ, на ваш взгляд, более понятен детям начальных классов? Какой предпочли бы Вы? Почему?
2. Дана задача: «8 одинаковых мячей стоят 48 грн. Сколько стоят 12 таких мячей?» Решите задачу любым способом. Запишите решение задачи всеми возможными способами.
3. Дана задача: «На ткацкой фабрике за 10 дней выпущено 80000 м ткани, причем каждый день выпускали одинаковое количество ткани. Сколько ткани будет выпущено за 100 дней при той же дневной норме?» Решите задачу любым способом. Покажите возможные варианты проверки решения задачи:
4. Составьте к данной задаче все возможные обратные: «В 5 одинаковых клетках помещается 15 кроликов. Сколько нужно таких клеток, чтобы поместить в них 42 кролика?»
5. Дана задача: «Из города к зимовке, расстояние между которыми 150 км, выехали аэросани со скоростью 60 км/ч. В то же время навстречу им из зимовки вышел лыжник и встретил аэросани через 2 часа. Найди скорость лыжника».
Перед решением этой задачи дети решали устные упражнения:
а) Два пешехода вышли одновременно навстречу друг другу и встретились через 2 часа. Сколько времени был в пути первый пешеход?
б) Два пешехода сближаются со скоростью 9 км/ч. Скорость первого пешехода 4 км/ч. Какова скорость второго пешехода?
в) Расстояние 150 км пройдено за 3 часа. Что можно узнать по этим данным?
Установите цель каждого упражнения. Составьте еще 2 упражнения, подготавливающие учащихся к решению этой задачи.
6. Дана задача: «За одно и то же время теплоход прошел 216 км, а моторная лодка 72 км. Чему равна скорость теплохода, если скорость моторной лодки 24 км/ч?» Проанализируйте задачу. Оцените, с какими трудностями может встретиться ребенок при ее решении. Создайте серию подготовительных упражнений к этой задаче. Позаботьтесь при этом, чтобы дети нашли все способы ее решения.
7. Задачу из предыдущего упражнения переделайте в задачу на пропорциональное деление. Смогут ли дети решить такую задачу в начальных классах? Обоснуйте ответ. Предусмотрено ли решение таких задач программой?
8. Дети самостоятельно решили задачу: «За два дня самолет пролетел с одинаковой скоростью 10240 км. В первый день он был в полете 10 ч, во второй – 6 ч. Сколько километров пролетал самолет каждый день?»
После этого учитель предложил детям такие упражнения: «Переделать эту задачу в задачу на нахождение четвертого пропорционального и сформулировать ее текст. Переделать в задачу на нахождение неизвестного по двум разностям и сформулировать ее текст. Изменить задачу так, чтобы ее решение сохранилось, но вместо величин скорость, время и расстояние в ней была другая тройка величин». Как вы думаете, каковы цели подобной работы? Какие у нее достоинства и недостатки? Подберите к этой задаче еще два упражнения с той же целью.
9. Предложите не менее трех различных способов проверки правильности решения задачи, данной в предыдущем упражнении, которыми могут воспользоваться дети. Нужно ли учить детей проверять задачи? Почему?
10. Учащимся на дом была задана задача: «Для школы купили 10 портретов по 3 грн. и 2 портрета по 5 грн. Сколько денег уплатили за все портреты?» Предложите косвенный способ проверки домашней задачи, приводящий детей к правилу умножения суммы на число. В чем преимущества такого способа проверки домашнего задания?
11. Дана задача: «В магазин привезли игрушки в пакетах: 90 кубиков по 10 штук в пакете и 60 кеглей по 6 штук в пакете. Сколько всего пакетов с игрушками привезли в магазин?» Детям дано упражнение на полное обращение этой задачи (составить и решить все обратные задачи). Выполните это упражнение, применив оптимальный вариант его записи.
Последующая и творческая работа над задачами
Сразу отметим, что многие методисты считают последующую и творческую работу над задачами аналогичными. На наш взгляд, это не верно. Во время последующей решению работы над задачей можно выполнять творческие задания, однако не всякая творческая работа над задачей является последующей решению.
При организации деятельности учащихся над задачей после ее решения (последующей) можно использовать следующие виды работы:
§ элементарное исследование решения задачи (при каких условиях задача имеет одно или несколько решений и не имеет решения; как будет изменяться ответ задачи, если изменять данные и т.д.);
§ сравнить решения обратных задач, пронаблюдать зависимости и т.д.;
§ изменить требование задачи так, чтобы задача решалась иначе;
§ составить другую задачу по вопросу данной;
§ составить аналогичную задачу, но с другими числами и другим сюжетом;
§ изменить требование задачи, но решение задачи осталось бы неизменным;
§ составить все возможные требования, которые можно поставить к данному условию и т.д.
При отработке навыков решения задач данного вида можно идти двумя путями: экстенсивным (количество) и интенсивным (качество). К сожалению, часто учителя жалеют время на последующую работу над задачей, решение обратных задач, работу над деформированными задачами, предпочитая отработку навыков решения задач программного минимума, т.е. идут экстенсивным путем. Выбор пути (интенсивный – экстенсивный) должен определяться типологическими особенностями учащихся и варьироваться для каждой группы (см. «Дифференцированная работа над задачами»).
Однако основным ориентиром в работе должен быть интенсивный путь. Можно привести такой пример: для того, чтобы ребенок понял, что такое «книга», можно много рассказывать о книгах, показывать их изображения и т.д. А можно просто дать ему книгу, чтобы он подержал в руках, полистал, подробно рассмотрел ее элементы и т.д. Во втором случае, понятие «книга» будет сформировано. А вот в перовом – проблематично. Также и с задачами. Решим большое количество задач одного вида – хорошо, но это совсем не означает, что у ребенка сформировался обобщенный способ решения этой задачи. А при решении обратных задач, деформированных задач, трансформации задач ученик как бы рассматривает задачу со всех точек зрения, преобразует ее, анализирует и синтезирует.
Приведем примеры творческих заданий, которые можно использовать на разных этапах работы над задачами.
1. Дано условие «Мальчик купил 10 марок, а девочка – 15». Какой из вопросов можно поставить к этой задаче: а) Сколько марок купили дети вместе? б) На сколько марок больше купила девочка? в) На сколько марок меньше купил мальчик? г) Сколько стоит одна марка?
2. Учащимся предлагаются несколько текстов задач, несколько кратких записей и решений. Задание следующее «К каждой задаче подберите ее краткую запись и решение. Реши оставшиеся задачи. Если осталась краткая запись, составь по ней задачу и реши ее». Количество задач, кратких записей и решений не должно совпадать. Это позволит исключить «остаточный принцип» выбора.
Например:
Задача 1. На площадке играли 5 мальчиков и 3 девочки. Сколько детей играли на площадке?
Задача 2. На площадке играли 5 мальчиков и 3 девочки. На сколько мальчиков больше, чем девочек?
Задача 3. На площадке играли 5 детей. 3 из них ушли. Сколько детей осталось на площадке?
Краткая запись 1
Было – 5
Ушли – 3
Осталось – ?
Краткая запись 2
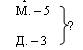
Краткая запись 3
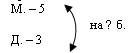
Краткая запись 4
Решение 1
5+3=8 (д.)
Решение 2
5–3=2 (р.)
3. На карточке записывается текст задачи и числовые выражения, составленные из числовых данных задачи. Детям предлагается выбрать те выражения или их комбинации, которые являются решением данной задачи.
Например:
Задача: «Три группы детей сделали к празднику каждая по 6 масок зверей и по 4 маски птиц. Сколько всего масок сделали дети?»
Выбери из предложенных все возможные решения данной задачи и вычисли значения.
| (6+4)·3 | 6·4 + 3 | 6·3 + 4·3 |
Данная задача решается двумя способами, учащийся должен увидеть оба из них и отбросить неподходящее выражение. Также можно добавить и такое задание: «По выражению, не являющемуся решением, составь задачу и реши ее».
Выделяются следующие методические приемы работы над задачами (М.В. Богданович, Н.Б. Истомина), которые, на наш взгляд, можно использовать для творческой работы над задачами.
1. Сравнение текстов, выявление структуры задач (неполные данные, избыточные данные).
2. Выбор схемы (по заданной схеме из нескольких задач выбрать соответствующую схеме задачу).
3. Выбор вопроса к задаче (дано условие, нужно выбрать из предложенных вопросов подходящий) или поставить собственный.
4. Выбор выражений для решения данной задачи (из предложенных выражений выбирают соответствующее решению).
5. Выбор или составление условия к заданному вопросу (дается вопрос задачи, учащимся предлагается или выбрать из приведенных условие или составить его самостоятельно).
6. Выбор данных (приводится текст неполной задачи, предлагается выбрать данные из предложенных или самостоятельно составить).
7. Изменение задачи для ее соответствия приведенному решению.
8. Постановка вопроса к готовому условию задачи в соответствии с приведенной схемой задачи.
9. Объяснение выражений, составленных по условию задачи (дается условие задачи и числовые выражения, составленные по условию, детям предлагается объяснить, что можно найти каждым из этих выражений).
10. Выбор решения задачи (дается текст задачи и решения, из которых нужно выбрать правильное).
Дата: 2018-12-28, просмотров: 1651.