Введем понятие задач с достаточным количеством данных, с недостающими данными и избыточными данными (по Н.В. Метельскому).

Если между условием задачи (А) и ее требованием (Х) установлено соотношение, определяющее одно или несколько определенных решений, то задачу считают определенной. Этот тип задачи можно условно изобразить формулой импликации: AÞX, которую будем понимать так: условие А содержит достаточно и только достаточно данных для выполнения требования Х.

Если из условия А опустить какое-либо данное ak, то получим задачу неопределенную (с недостающими денными), которая имеет бесконечное множество решений, зависящих от бесконечного множества значений той величины (параметра), которой принадлежало значение ak.

В случае, если условие, кроме А содержит еще некоторые данные an+1, то задачу называют переопределенной (с избыточными данными). Переопределенные задачи могут иметь решения в случае, если лишние данные не противоречат друг другу [19, c.176-177].

Нереальными задачами будем называть задачи, числовые данные которых делают их лишенными смысла (по В.А. Крутецкому). Каждая из этих задач является типовой, но числовые данные делают ее нереальной. Например:

1. Периметр прямоугольника 8 см, а сумма двух его сторон 6 см. Найти длину стороны.

2. Иван на два года моложе Петра, Петр четырьмя годами старше Степана, Андрей на три года старше, чем Петр, Иван равен по возрасту Степану. Кто старше – Андрей или Иван? [19, c.151].

Применение при обучении решению задач с недостающими и избыточными данными, нереальных задач имеет большое значение. При помощи этих задач можно не только выяснить насколько дети понимают связи в задаче, но и при работе над одной задачей с избыточными данными иногда удается составить и решить еще несколько задач, что является одним из приемов насыщения уроков задачами.

Например:

1. Маша отдала несколько открыток подруге, после чего у нее осталось 5 открыток. Сколько открыток отдала Маша подруге?

После выяснения, какого данного не хватает для возможности решения задачи, ученикам можно предложить самостоятельно подобрать, сколько открыток было у Маши, и решить при этом несколько задач вместо одной.

2. К чаю подали 9 пирожных «эклер», 6 пирожных «корзиночек» и 12 шоколадных конфет. Съели 11 пирожных. Сколько пирожных осталось?

Следует выяснить, какие данные лишние, как изменить вопрос или что изменить в условии, чтобы использовать все данные. Опять решается не одна, а несколько задач.

Задачи с избыточными данными могут быть противоречивыми и непротиворечивыми. На наш взгляд, детям обязательно нужно показывать такие задачи.

Рассмотрим работу над задачами такого вида на конкретных примерах. Даны задачи: а) «Дети сорвали 24 яблока. 8 яблок они съели, а остальные поделили поровну. Сколько яблок получил каждый ребенок?»; б) «Таня и Сережа сорвали 18 яблок. Таня сорвала 6 яблок, а Сережа в 2 раза больше. Сколько яблок сорвал Сережа?»; в) «Таня и Сережа сорвали 18 яблок. Таня сорвала 6 яблок, а Сережа в 3 раза больше. Сколько яблок сорвал Сережа?». Составим схемы разбора каждой из предложенных задач.

Задача а)

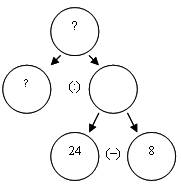
Задача (а) является задачей с недостающими данными. Она напоминает деформированную задачу, однако, в отличие от деформированной задачи, не имеет «окошка», т.е. конкретного указания на то, что пропущено данное. Эту задачу можно использовать для составления каскада задач.

Задачи (б) и (в) являются задачами с избыточными (лишними) данными. Однако одна из них может быть решена и непротиворечива, а другая не имеет однозначного решения, данные в ней противоречат друг другу.

Задача б)

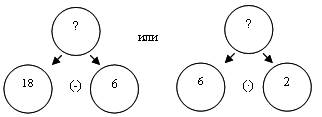
Данная задача, решенная с использованием каждой пары данных, дает одинаковый ответ (12 яблок сорвал Сережа). Таким образом, эта задача не содержит противоречивых данных.

Задача в)

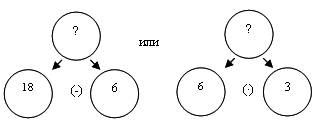
Эта задача, решенная с использованием каждой пары данных, дает разные ответы, которые противоречат друг другу: Сережа сорвал 12 яблок, и Сережа сорвал 18 яблок. Таким образом, задача не имеет однозначного решения.

Однако, иногда случается так, что дети принимают полную задачу за задачу либо с лишними, либо недостающими данными.

Например:

1. Турист 3 ч шел пешком со скоростью 5 км/ч, потом 4 ч ехал на поезде, скорость которого в 12 раз больше, а оставшийся путь он проехал на автобусе за 8 ч. С какой средней скоростью двигался турист, если скорость автобуса равна 3/4 скорости поезда?

В этой задаче нужно найти скорости движения туриста на каждом из этапов пути, найти все расстояние, пройденное туристом, и разделить это расстояние на общее время в пути.

Однако, дети, видя скорость движения на каждом этапе, часто хотят найти не среднюю скорость за все время движения, а среднюю скорость на трех этапах, ища среднее арифметическое трех скоростей, т.е., по представлению детей данная задача является как бы задачей с избыточными (лишними) данными.

2. Через один кран бассейн заполняется за 15 часов, а через другой – за 10 часов. За сколько часов заполнится бассейн, если краны будут работать вместе?

При решении этой задачи нужно обозначить объем бассейна за 1, потом найти производительность 1-го крана и 2-го крана, потом результаты сложить. Но учащиеся начальной школы, не знакомые с обыкновенными дробями, посчитают эту задачу как задачу с недостающими данными.

Включение задач с лишними и недостающими данными в курс математики в начальных классах является и одной из составляющих формирования навыков контроля и самоконтроля младших школьников, на основе которых у учащихся в дальнейшем формируются критерии, позволяющие учащимся самостоятельно находить ошибки в решениях заданий (не только текстовых задач). К ним можно отнести следующие критерии:

§ соотношение результата с действительностью;

§ соотнесение полученного результата с данными задачи и сравнение с первоначально ожидаемым результатом;

§ проведение операций в обратном порядке;

§ исследование ответа в предельных ситуациях (что будет, если….);

§ решение задания другим способом и сверка результатов;

§ проверка хода решения с обращением внимания на следующее: а) все ли данные использованы; б) достаточно ли данных для решения; в) не нарушена ли логика решения; г) не используются ли в решении те сведения, которые не вытекают непосредственно из условия задачи; д) прослеживается ли логика решения.

Также можно предложить детям задачи с вопросом, в котором спрашивается то, что уже известно в задаче. Например: «На грядку высадили 15 кустов смородины и 5 кустов крыжовника. Сколько кустов крыжовника высадили?» Применение задач такого рода также позволяет ученикам глубже осмыслить понятие задачи, ее структуры.

Упражнения

1. Найдите в действующих учебниках математики задачи с недостающими данными. Как вы думаете, почему они расположены именно в разделе «Занимательные задачи»?

2. Дана задача: «Пальто, костюм и ботинки стоят 100 грн. Пальто стоит 50 грн., костюм 38 грн. Сколько стоят ботинки?» Сделайте схему разбора этой задачи. Переделайте эту задачу в задачу с недостающими данными; в задачу с лишними данными; в противоречивую задачу. Как все это отражается на схеме разбора задачи? В чем ценность таких задач? Какая из переделанных задач способна дать серию задач при работе с ней?