Некоторые авторы относят составление краткой записи к задаче к этапу поиска способа решения задачи, а не к этапу анализа условия задачи (М.А. Бантова). На наш взгляд, это действительно так, т.к. составление краткой записи задачи часто позволяет определить ее решение (неявный поиск способа решения).
Работая над планом решения задачи, ученик должен выделить все возможные связи между величинами, которые прослеживаются в данной задаче (даже, если затем их не нужно будет задействовать в решении).
Во время разбора задачи можно составить иллюстрацию к ней. Иллюстрация к задаче, её краткая запись, составление схемы или чертежа, таблицы являются вспомогательными средствами, но, чаще всего именно они помогают ученику вникнуть в смысл задачи, выявить зависимости между величинами и найти план решения задачи.
Краткая запись, выступая в роли наглядной и словесной опоры для памяти учеников, способствует более быстрому и всестороннему усвоению задачи, осмыслению числовых данных. Выделение из текста числовых данных и их рациональная запись делает более ясным то, что дано в задаче и что в ней отыскивается. Краткая запись дает возможность расчленить задачу на условие и искомое, облегчает анализ задачи.
Однако следует помнить о том, что краткая запись служит интересам ребенка при решении задачи, а не целью при решении (вспомогательное средство!!!). В соответствии с современными требованиями Министерством образования и науки Украины совместно с лабораторией обучения и воспитания младших школьников Института педагогики АПН Украины разработаны «Методические рекомендации к устной и письменно речи младших школьников. Нормы оценки знаний, умений и навыков», в которых отмечается, что недопустимо снижать отметку ребенку при решении задачи, если краткая запись выполнена не так, как этого требует учитель или не выполнена совсем. Поэтому, при оценивании правильного решения задачи не следует осуждать ребёнка за то, что он сделал краткую запись не по образцу, показанному учителем, а так, как ему удобно, главное, что задача решена правильно. Мне как маме двух детей, не раз приходилось сталкиваться с проблемой: ребенок уже решил задачу, проанализировав ее, пронаблюдав все связи, выполнив необходимые действия, получил ответ, но никак не может составить именно краткую запись. Иногда это заканчивалось слезами, иногда – нежеланием дальше работать над данной задачей.
М.В. Богданович выделяет следующие виды краткой записи задач: схема, таблица, чертеж. К стандартным (видовым) задачам обычно используется стандартная схема, однако, если ребенок использует свою схему, то нельзя ему этого запрещать. Таблицей оформляют краткую запись задач с пропорциональными величинами, задачи на движение обычно иллюстрируют чертежом и таблицей.
При обучении детей выполнению краткой записи важно научить детей систематизировать и располагать данные так, чтобы наиболее выпукло показать сопоставление различных величин, причем показывать как можно больше различных вариантов.
Например, задачи на нахождение остатка чаще всего записываются кратко таким образом:
Было – …
Взяли (потратили, израсходовали, и т.д.) – …
Осталось – ?.
Приведем различные формы краткой записи задач такого вида.
«В коробке было 24 карандаша. Мальчик взял 12 карандашей. Сколько карандашей осталось в коробке?»
Краткая запись может выглядеть так:
1) Было – 24 к.
Взял – 12 к.
Осталось – ?
Это стандартная форма краткой записи, хотя, на наш взгляд, целесообразнее было бы использовать краткую запись в виде схемы или чертежа, так как они подчеркивают связь действий сложения и вычитания, их обратность, позволяют проверить решение задачи и являются более универсальными:
2)
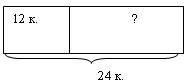
3)
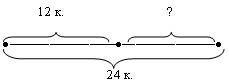
4) Схема на основе схем С.Н. Лысенковой
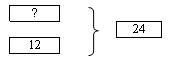
При разборе задачи графическая иллюстрация имеет большое значение. В психологическом исследовании М.Э. Боцманова показала её значение и выделила этапы применения. Она пишет: «Трудности в решении задач обусловлены тем, что для детей слишком значительным представляется разрыв между конкретной ситуацией, отраженной в сюжетной задаче и её абстрактной стороной – математической структурой. Применение графической наглядности способствует преодолению этого разрыва, поскольку любое графическое выражение сочетает в себе черты абстрактного и конкретного. Являясь абстрагированным и обобщенным выражением закономерностей, оно переводит решение задачи в конкретный план». На основании этого исследования было установлено, что эффективными средствами для решения задачи являются предметно-аналитическая картинка – схема – чертёж.
Сначала учащимся предлагается предметно-аналитическая картинка (изображение предметов из задачи с анализом связей), затем вводится схема с использованием картинки, далее осуществляется переход к самостоятельному созданию школьниками графической схемы.
Например, рассмотрим задачу: «С первого участка было собрано 5 одинаковых корзин моркови, а со второго – три такие же корзины, причем с первого участка собрали на 30 кг моркови больше, чем с первого. Сколько килограммов моркови собрали с каждого участка?»
На доске сначала вывешивается картинка, изображающая корзины с морковью, причем можно пронаблюдать, что участка два, корзин на первом – 5, на втором – 3, и отмечено, что с первого собрано на 30 кг больше.

На основании этого рисунка учащиеся видят, что со второго участка собрали на 2 корзины больше, дальше они соотносят их с 30 кг и делают вывод, что масса двух корзин 30 кг. Однако, в тетради рисовать корзины слишком долго, поэтому детям вместо корзин предлагается начертить прямоугольники (круги, квадраты и т.д.), т.е. заменить предметную картинку схемой. Предметная иллюстрация помогает создать у детей яркую картину ситуации в задаче, однако стоит ли её использовать постоянно?
Далее можно количество корзин изобразить отрезками разной длины и схема превратится в чертеж:
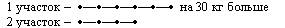
Данная задача будет решаться детьми намного быстрее, если научить их оформлять подобные схемы таким образом:

Умение иллюстрировать задачу при помощи таких схем позволит детям в дальнейшем без труда составлять схемы для решения задач «на части» (на нахождение чисел по их сумме и разности, сумме и отношению и т.д.) в пятом классе. Например, рассмотрим возможные варианты схем к задаче «Кусок сатина длиной 48 м нужно разрезать на две части так, чтобы одна из них была длиннее другой в 3 раза. Сколько метров сатина будет в каждом куске?»
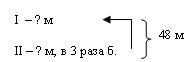
Данная схема не позволяет сразу увидеть решение задачи. Типичная ошибка учащихся при решении таких задач та, что для нахождения длины первого куска они делят сумму (48) на отношение (3). При этом если ребенок приучен делать проверку задачи, то он заметит свою ошибку. Если же нет, то задача так и остается решенной неправильно.
Однако работу можно провести так: Что дано в условии? (Сумма длин кусков сатина (48 м) и их отношение (длина одного куска в 3 раза больше длины другого)). Пусть длина меньшего куска составляет одну часть, тогда длина второго куска 3 таких же части. Изобразим это на схеме:
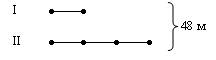
Важным при составлении схемы является то, чтобы отрезки-части совпадали по длине, и чтобы начала этих отрезков лежали на одной вертикали. По схеме сразу можно увидеть, сколько одинаковых частей приходится на сумму. Решение задачи облегчается.
Составление схемы позволяет преодолеть разрыв между абстрактным и конкретным. При помощи правильно оформленной и расположенной схемы есть возможность сразу проследить связи между искомыми и данными, наметить план решения или решить задачу.
Рассмотрим задачу, в которой различные расположения схемы позволяют найти различные способы решения.
«Масса двух еловых шишек и одного желудя – 152 г. А масса двух желудей и одной еловой шишки – 94 г. Найти массу одной шишки, одного желудя. Что тяжелее: одна еловая шишка или один желудь и на сколько? (СНОСКА: За основу взята задача из статьи Махрова В.Н. Рисунок помогает решать задачи // Начальная школа. - 1997. - №7.– С.70. Способ 1 предложен Махровой В.Н., способы 2 и 3 – автором пособия)
Способ 1
Изобразим условие задачи в виде схемы:

Расположим схемы следующим образом

(из этого расположения схем сразу следует 94 г способ 2)
Из рисунка видно, что масса шишки больше массы желудя.
Далее рассуждаем так: если бы у нас было 4 шишки и 2 желудя, то масса их будет в два раза больше, т.е. 304 г.
1) 152×2 = 304 (г)
Схему изобразим так:

Из схемы видно, что на три шишки приходится
2) 304 – 94 = 210 (г)
Отсюда масса одной шишки
3) 210:3 = 70 (г)
Далее, если бы у нас было 4 желудя и 2 шишки, то их общая масса составит
4) 94×2 = 188 (г).
Отсюда следует, что масса трех желудей 36 г
5)188–152 = 36 (г), а масса одного желудя 12 г
6) 36:3=12 (г).
Осталось только найти, насколько шишка тяжелее желудя
7) 70 –12 = 58 (г).
Ответ: масса желудя 12 г, масса шишки 70 г. Шишка тяжелее желудя на 58 г.
Задача решена в 7 действий. Таким образом, способ 1 не самый удачный, на наш взгляд.
Во втором способе задача решается в 4 действия.
Способ 2
Расположим схему таким образом:

Из схемы видно, если убрать из каждого набора по шишке и желудю, то останется шишка и желудь. Теперь перейдем к массам этих объектов. Если от массы двух шишек и желудя отнять массу двух желудей и шишки, то полученный результат покажет разность масс шишки и желудя. Таким образом, ответ на вопрос «На сколько тяжелее?» будет получен. Что тяжелее – шишка или желудь видно из рисунка. Выполним вычисления:
1) 152 – 94 = 58 (г).
Далее, если мы к массе двух шишек и одного желудя добавим полученную разность, то мы получим массу трех шишек:
2) 152 + 58 = 210 (г).
Отсюда масса шишки
3) 210:3 = 70 (г),
а масса желудя
4) 70 – 58 = 12 (г).
Ответ: масса желудя 12 г, масса шишки 70 г. Шишка тяжелее желудя на 58 г.
Способ 3
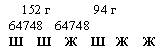
Из схемы видно, что у нас всего 3 шишки и 3 желудя (это можно определить пересчитыванием, либо оформить двумя арифметическими действиями), общая масса которых составляет
1) 152 + 94 = 246 (г).
Масса пары (желудь–шишка) составляет
2) 246:3 = 82 (г).
Можно составить еще одну схему (по необходимости)

из которой видно, что масса одной шишки может быть получена следующим образом:
3) 152 – 82 = 70 (г).
Далее находим массу желудя:
4) 82 – 70 = 12 (г).
5) 70 – 12 = 58 (г)
Ответ: масса желудя 12 г, масса шишки 70 г. Шишка тяжелее желудя на 58 г.
Обучение детей схематизации задач и составлению краткой записи представляет собой целенаправленный достаточно длительный процесс. Схематизация каждой из задач не является однозначной, составление схемы – процесс индивидуальный. Однако обучение использованию различных вариантов схематической записи задачи иногда позволяет ребенку увидеть разные способы решения задачи
Интересную методику обучения схематизации задач при помощи приема противопоставления различных форм наглядной интерпретации задач, предлагает Н.Б. Истомина (в учебниках математики Н.Б. Истоминой).
Использование элементов данной методики при работе по традиционным программам позволит усовершенствовать умения и навыки учеников по решению задач.
В процессе этой работы у учащихся должно быть выработано умение чертить отрезки, складывать и вычитать отрезки; умение описывать предметные и текстовые ситуации, схематизировать и математизировать их.
Два ученика Маша и Миша иллюстрируют тексты задач, при этом каждые по-разному. В одном из ответов содержится типичная ошибка, допускаемая детьми. При этом, на наш взгляд, можно показывать одновременно и несколько правильных интерпретаций.
Необходимо проводить работу, направленную на понимание соотношения целого и его частей. Со старшими дошкольниками по формированию элементарных математических представлений такая работа проводилась. С первоклассниками ее можно организовать на примерах отрезков.
Например:
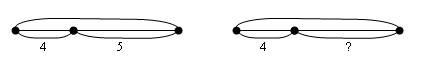
«Посмотри на схему. Что будешь искать: целое или часть?»
После введения понятия буквенного выражения можно использовать схемы с буквами. Также можно использовать и такие упражнения: «В корзине 15 грибов. Из них 5 белых, а остальные лисички. Обозначь все грибы кругами и покажи, сколько в корзине лисичек» (СНОСКА: Истомина Н.Б., Нефедова И.Б. Первые шаги формирования умения решать задачи // Начальная школа. – 1998. - №11-12. - С.42-48)
Маша выполнила задание так:

А Миша так:

Кто выполнил задание верно?
Однако, к помощи Миши и Маши авторами приема рекомендуется прибегать только тогда, когда учащиеся сами не могут справиться с заданием.
Рассмотрим составную задачу: «В вазе 15 конфет. Из них 4 шоколадных, 5 ирисок, а остальные – леденцы. Сколько леденцов в вазе?»
Стандартная модель (краткая запись) выглядит так:
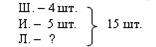
От исходной модели можно перейти непосредственно к схемам решения:

Или
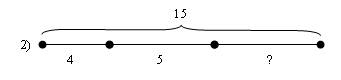
На наш взгляд, последняя схема позволит быстро найти путь к решению задачи.
Многоступенчатость составления краткой записи позволяет ребенку рассмотреть задачу со всех «сторон», позволяет найти различные способы решения задач.
Также можно обучать учеников составлению графов-моделей (схем) задачи (СНОСКА: Подробнее: Белошистая А.В. Прием графического моделирования при обучении решению задач. // Начальная школа. – 1991. - № 4. – С.18 -24), начиная с решения простых задач на нахождение суммы и остатка.
Идея построения граф-схемы задачи основывается на том, что в условии задачи рассматриваются связанные зависимостью элементы. Эти зависимости выражаются отношениями, которые обычно связывают три величины. Такие связанные тройки величин представляют собой либо простую задачу, либо простые задачи, входящие в составную задачу. Они и являются основными компонентами структуры задачи. Схематично каждая из связок представляется в виде своеобразного «треугольника». Структура составной задачи на схеме обычно выглядит как объединение конечного числа таких «треугольников».
Например, рассмотрим задачи «В коробке было 5 карандашей. Миша положил туда еще 2 карандаша. Сколько карандашей стало?» и «В коробке лежало 5 карандашей. 2 карандаша взяли. Сколько карандашей осталось в коробке?».
Разбор задач на нахождение суммы и остатка проведем от данных к вопросу и от вопроса к данным, при этом, обучая детей составлять схемы разбора и решения задачи. В схемах можно использовать также и знаки арифметических действий, что позволяет трансформировать их в план-схему решения задачи.
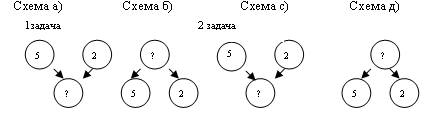
Схемы (а) и (с), а также (б) и (д) совпадают. Практически по каждой из схем можно составить два числовых выражения со знаком (+) и (–). Поэтому детям можно предложить добавить в схемы знаки арифметических действий, чтобы схема относилась к конкретной задаче.
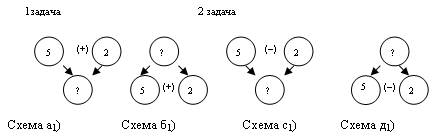
При обучении детей составлению граф-схем необходимо помнить, что схема составляется не после того, как задача прочитана детьми и проанализирована, а во время чтения текста и анализа условия. Таким образом, сначала появляется схема типа (а) – (д), а затем они трансформируются в схемы (а1) – (д1).
Упражнения
1. Пронаблюдайте в учебниках [Б1], [Б2], [Б3] как вводятся различные виды краткой записи задач, граф-схемы разбора задач.
2. Составьте и решите такую составную задачу, чтобы она содержала в себе следующие две простые задачи: а) увеличение числа в несколько раз; б) нахождение суммы.
3. Даны задачи: «Масса дыни 1 кг 200 г. Ваня съел 1/6 дыни, а Маша – 1/5 дыни. На сколько граммов дыни больше съела Маша?» и «У Андрея 123 марки, это в 3 раза больше, чем у Алеши. На сколько марок у Алеши меньше, чем у Андрея?» Запишите задачи кратко, решите по действиям. Сделайте схемы разбора задач. Выделите на схеме простые задачи. Определите их вид.
4. Составьте схему для решения задачи и решите ее арифметически: «Для изготовления стекла для бутылок берут 25 частей кварцевого песка, 9 частей соды, а извести на 4 части меньше, чем соды. Сколько надо взять песка, если извести и соды взяли 700 ц?»
Дата: 2018-12-28, просмотров: 3384.