Перед исключением 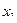 отыскивается
отыскивается 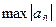 по
по 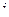 . Допустим, максимум соответствует
. Допустим, максимум соответствует 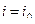 . Тогда первое уравнение в исходной системе меняем местами с
. Тогда первое уравнение в исходной системе меняем местами с 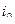 уравнением. После этого осуществляем первый шаг исключения. Затем перед исключением
уравнением. После этого осуществляем первый шаг исключения. Затем перед исключением 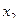 из оставшихся уравнений отыскиваем
из оставшихся уравнений отыскиваем 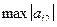 , где
, где 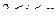 , осуществляется соответствующая перестановка уравнений.
, осуществляется соответствующая перестановка уравнений.
Можно показать, что условие диагонального преобладания остается справедливым после каждого шага исключений в процессе приведения матрицы к треугольному виду, т.е.
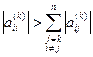 , для всех
, для всех 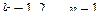 . (2.17.5)
. (2.17.5)
Это означает, что перед каждым исключением очередной неизвестной главный элемент будет находиться в «нужной позиции».
Рассмотренные модификации метода Гаусса позволяют, как правило, существенно уменьшить влияние погрешности округления на результаты расчетов.
Пример 2.2.17.1. Методом Гаусса с выбором ведущего элемента по столбцам решить систему:
Решение.
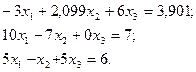
1. Прямой ход. Реализуем поиск ведущего элемента по правилу: на 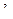 -м шаге переставляются
-м шаге переставляются 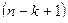 оставшихся уравнений так, чтобы наибольший по модулю коэффициент при
оставшихся уравнений так, чтобы наибольший по модулю коэффициент при 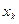 попал на главную диагональ:
попал на главную диагональ:
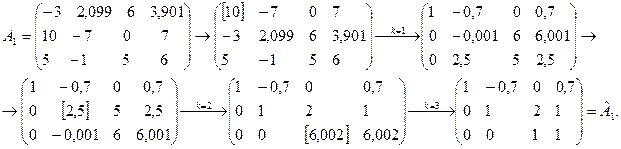
2. Обратный ход. По матрице 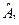 составим систему уравнений:
составим систему уравнений:
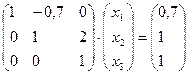 или
или 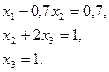
Решая ее, последовательно получаем: 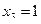 ,
, 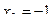 ,
, 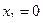 .
.
Метод простой итерации
Для решения систему линейных уравнений  приводим к каноническому виду:
приводим к каноническому виду:
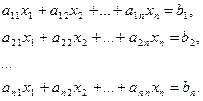 (2.17.6)
(2.17.6)
Выразим 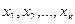 :
:
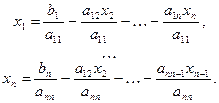
Таким образом, получим 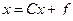 , где
, где

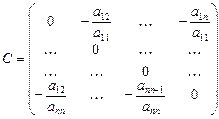 ,
, 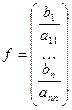 ,
, 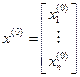 . (2.17.7)
. (2.17.7)
Итерационный процесс запишется виде:
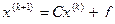 . (2.17.8)
. (2.17.8)
Начальное приближение 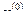 выбирается произвольно, но требуется выполнение условия сходимости, норма матрицы
выбирается произвольно, но требуется выполнение условия сходимости, норма матрицы 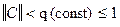 . Сходящийся процесс обладает свойством самоисправляемости. Условие сходимости выполняется, если в матрице
. Сходящийся процесс обладает свойством самоисправляемости. Условие сходимости выполняется, если в матрице 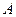 диагональные элементы преобладают. Иначе модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов. Чем меньше величина нормы матрицы
диагональные элементы преобладают. Иначе модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов. Чем меньше величина нормы матрицы 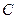 , тем быстрее сходится метод.
, тем быстрее сходится метод.
Для того чтобы данный процесс сходился, необходимо, чтобы норма матрицы 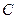 была меньше 1 или выполнялись следующие условия:
была меньше 1 или выполнялись следующие условия:
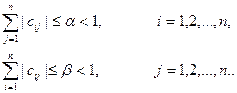 (2.17.9)
(2.17.9)
Тогда справедливы оценки скорости сходимости:
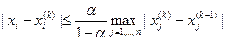 ,
,
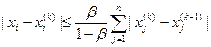 . (2.17.10)
. (2.17.10)
Методика решения систем линейных уравнений
методом простой итерации
1. Преобразовать систему  к виду
к виду 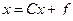 .
.
2. Проверить условие сходимости 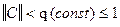 . Задать начальное приближение
. Задать начальное приближение 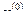 и точность
и точность 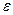 . Положить
. Положить 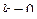 .
.
3. Вычислить приближение по формуле 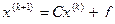 .
.
4. Если выполнено условие 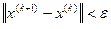 , то процесс завершить и положить
, то процесс завершить и положить 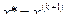 , иначе
, иначе 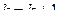 перейти к пункту 3.
перейти к пункту 3.
Пример 2.2.17.2. Для системы линейных алгебраических уравнений построить сходящийся итерационный процесс:
Решение.
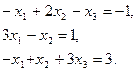
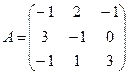 .
.
Матрица этой системы не имеет диагонального преобладания.
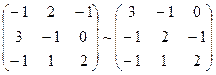 .
.
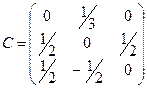 ,
, 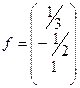 ,
, 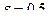 .
.
Достаточное условие сходимости метода простых итераций 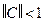 выполняется. Поэтому сначала проведем преобразование.
выполняется. Поэтому сначала проведем преобразование.
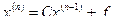 .
.
Возьмем
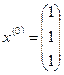 , тогда
, тогда
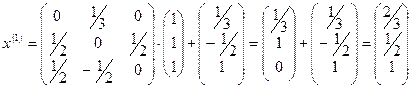 ,
,
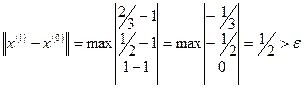 ,
,
 ,
,
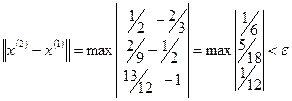 .
.
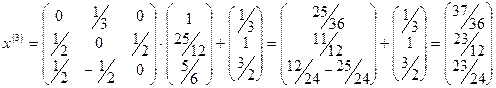 ,
,
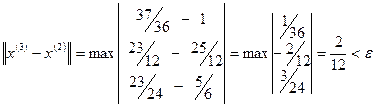 .
.
Видно, что норма разности между двумя последовательными приближениями с увеличением номера итерации уменьшается, что характеризует сходящийся процесс (этот вывод относится ко всем приведенным примерам). Видно также, что, начиная со 2-й итерации, 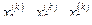 с увеличением
с увеличением 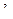 увеличиваются и уменьшаются соответственно, и они стремятся к верному (точному) решению:
увеличиваются и уменьшаются соответственно, и они стремятся к верному (точному) решению: 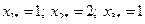 .
.
2.2.18 Нахождение наибольшего по модулю
собственного числа матрицы
Корни характеристического уравнения 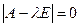 являются
являются 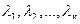 собственными значениями матрицы
собственными значениями матрицы 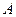 .
.
Пусть 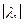 наибольший по модулю. Матрица с действительными и положительными коэффициентами имеем наибольшее действительное собственное значение.
наибольший по модулю. Матрица с действительными и положительными коэффициентами имеем наибольшее действительное собственное значение.
В качестве начального собственного вектора возьмем произвольный вектор 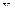 . Тогда
. Тогда 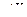 назовем итерацией вектора
назовем итерацией вектора 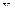 , которая образуется путем перемножения
, которая образуется путем перемножения 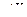 ,
, 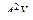 , …,
, …, 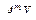 ;
;
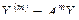 .
.
Приближенное наибольшего по модулю собственного значения:
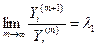 ,
, 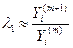 , при
, при 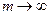 .
.
Для ускорения сходимости можно составить последовательность 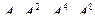 и т.д.
и т.д.
Методика решения задачи нахождения наибольшего
собственного значения матрицы
1. Выбрать произвольное начальное приближение собственного вектора 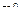 ,
, 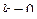 .
.
2. Найти 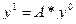 ,
, 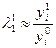 , где
, где 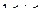 и
и 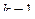 .
.
3. Вычислить 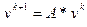 .
.
4. Найти 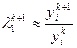 , где
, где 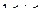 .
.
5. Если 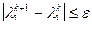 , то процесс завершить и положить
, то процесс завершить и положить 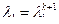 , иначе
, иначе 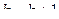 и перейти к п.3.
и перейти к п.3.
Пример 2.2.18.1. Найти наибольшее собственное значение матрицы 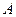
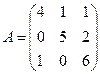 , с точностью
, с точностью 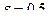 .
.
Решение.
Пусть 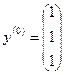 , тогда значение наибольшего собственного значения на нулевой итерации равно
, тогда значение наибольшего собственного значения на нулевой итерации равно 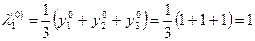 ,
,
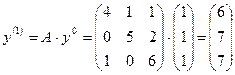 .
.
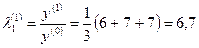 ,
,
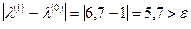 .
.
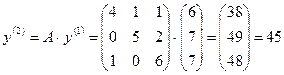 ,
,
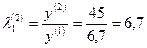 ,
,
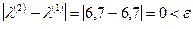 .
.
Дата: 2018-12-28, просмотров: 676.