Пусть дано нелинейное уравнение 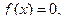 где
где 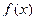 – нелинейная функция, определена и непрерывна на некотором промежутке
– нелинейная функция, определена и непрерывна на некотором промежутке 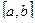 . Требуется найти корни уравнения.
. Требуется найти корни уравнения.
Решение осуществляется в два этапа:
I. Отделение корней, нахождение отрезков 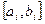 , внутри которых содержится один простой или кратный корень.
, внутри которых содержится один простой или кратный корень.
Если функция 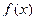 определена, непрерывна на отрезке
определена, непрерывна на отрезке 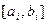 , и имеет конечную производную, причем на концах отрезка
, и имеет конечную производную, причем на концах отрезка 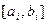 значения функции имеют разные знаки (
значения функции имеют разные знаки ( 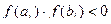 ), и ее первая производная сохраняет знак внутри отрезка
), и ее первая производная сохраняет знак внутри отрезка 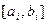
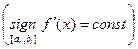 , тогда на
, тогда на 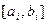 находится только один корень
находится только один корень 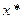 на
на 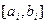 , удовлетворяющий уравнению
, удовлетворяющий уравнению 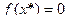 .
.
Графический способ отделения корней – построение графика функции применяется наиболее часто, но не обладает большой точностью. Часто бывает удобно заменить уравнение 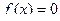 на равносильное
на равносильное 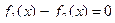 , с формированием простых функций
, с формированием простых функций 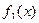 и
и 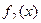 и дальнейшим построением графиков этих функций. Корнями уравнения являются абсциссы точек пересечения графиков
и дальнейшим построением графиков этих функций. Корнями уравнения являются абсциссы точек пересечения графиков 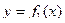 и
и 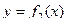 .
.
Пример 2.2.16.1. Задано уравнение 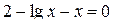 , отделить корень уравнения.
, отделить корень уравнения.
Решение.
Представим данное уравнение в виде 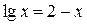 и построим графики функций
и построим графики функций 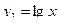 и
и 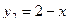 . Абсцисса точки
. Абсцисса точки 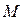 пересечения этих графиков находится в промежутке
пересечения этих графиков находится в промежутке 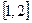 (рис. 16.1), поэтому начальное значение принадлежит этому отрезку.
(рис. 16.1), поэтому начальное значение принадлежит этому отрезку.

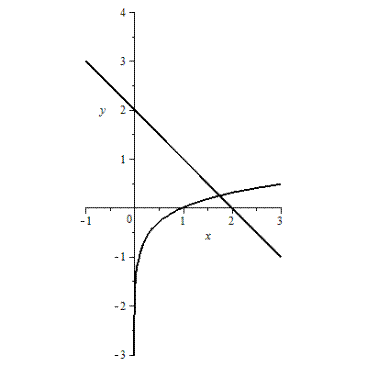
Рис. 16.1
Пример 2.2.16.2. Задано уравнение 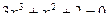 , отделить корень уравнения.
, отделить корень уравнения.
Решение.
Графический способ:
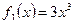 ,
,
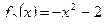 .
.

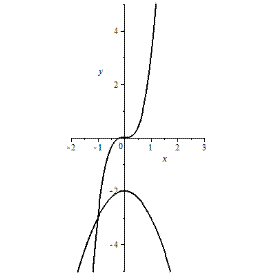
Ответ: 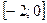 .
.
Аналитический способ – построение графика функции на основе исследования функции выделить интервал, на котором лежит один корень.
II. Уточняется начальное значение корня уравнения, выбранного из 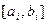 , до заданной точности одним из численных методов, в котором реализуются последовательные приближения.
, до заданной точности одним из численных методов, в котором реализуются последовательные приближения.
Пример 2.2.16.3. Задано уравнение 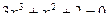 , отделить корень уравнения.
, отделить корень уравнения.
Решение.
Аналитический способ решения:
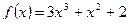 ,
,
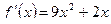 ,
,
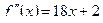 .
.
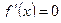
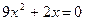 ,
,
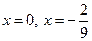 .
.
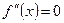
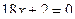 ,
,
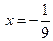 .
.
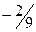
| 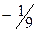
| 0 | |||||

| + | 0 | – | – | 0 | + | |
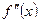
| – | – | 0 | + | + | ||
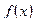
| 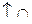
| 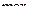
| 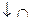
| т.перегиба | 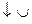
| 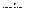
| 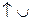
|

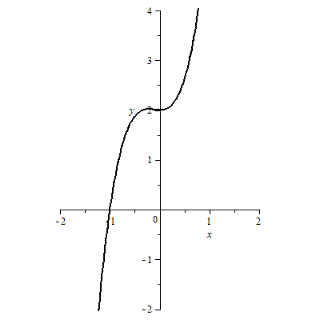
Ответ: 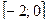 .
.
Метод половинного деления
Пусть дано нелинейное уравнение 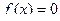 и отделен простой корень
и отделен простой корень 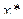 на отрезке
на отрезке 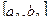 , выполняется условие
, выполняется условие 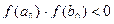 и
и 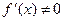 ,
, 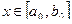 и
и 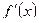 сохраняет знак. Требуется уточнить местоположение корня уравнения с заданной точностью
сохраняет знак. Требуется уточнить местоположение корня уравнения с заданной точностью  .
.
Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности 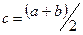 , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция
, и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция 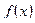 принимает различные знаки.
принимает различные знаки.
Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины  , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
, задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
Метод имеет линейную, но безусловную сходимость, его погрешность за каждую итерацию уменьшается в 2 раза:
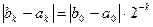 .
.
Методика решения нелинейного уравнения
методом половинного деления
1. Найти начальный интервал неопределенности 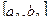 одним из методов отделения корней, задать малое положительное число
одним из методов отделения корней, задать малое положительное число  и присвоить
и присвоить 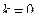 .
.
2. Найти середину текущего интервала 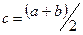 .
.
3. Если 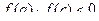 , то
, то 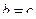 , иначе
, иначе 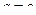 .
.
4. Если 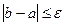 , то процесс завершить:
, то процесс завершить: 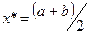 , иначе
, иначе 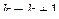 и перейти к п.2.
и перейти к п.2.
Пример 2.2.16.4. Найти корень уравнения методом половинного деления 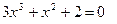 с точностью
с точностью 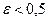 на интервале
на интервале 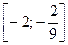 .
.
Решение.
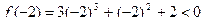 ,
,
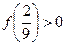 ,
,
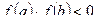 ,
,
1) 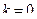 ,
, 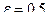 .
.
2) 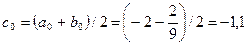 .
.
Если 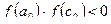 , тогда
, тогда 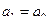 ,
, 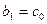 , иначе
, иначе 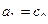 ,
, 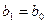 .
.
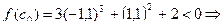
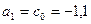 ,
, 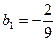 .
.
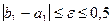
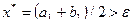 , иначе
, иначе 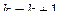 .
.
2) 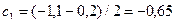 ,
,
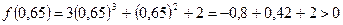 ,
,
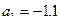 ,
,
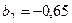 ,
,
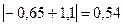 ,
,
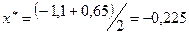 .
.
Дата: 2018-12-28, просмотров: 426.