Комплекс операций для достижения определенной цели является проектом. Процесс выполнения проекта отображается сетевым графиком.
В сетевом планировании проекта применяется сеть – конечный граф без петель, у которого существует одна вершина – вход и одна вершина – выход. Вершины графа интерпретируются как события хода проекта, дуги – операции, работы.
Сеть отражает порядок выполнения операций, дугам присваиваются характеристики – время выполнения операции или ее стоимость.
После построения сетевого графика проекта возникает вопрос о времени выполнения всего комплекса операций. Это время не может быть меньше длительности операций самого неблагоприятного пути в сети – критического пути. Вычисление критического пути проводится по алгоритму поиска максимального времени от начала сети до конца. Каждому узлу присваивается индекс, соответствующий максимальному времени от начала сети.
Индекс последнего узла является временем выполнения проекта. Для определения критического пути осуществляют обратный проход от конца к началу сети, восстанавливается, по каждому пути получен индекс данного узла.
Операции критического пути не меняют времени выполнения, в некритических операциях возможно изменение времени выполнения в определенных пределах, так чтобы это изменение не отражалось на критический путь.
Длительность операций не является детерминированной величиной, эксперты определяют минимальное, максимальное и наиболее вероятностное время выполнения операции.
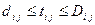
где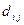 
и 
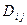– границы возможного изменения времени операций;
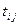– принятое время выполнения операций (вероятностное время).
Если ускорить время каждой операции, то проект будет «срочным», но с большой стоимостью. За счет увеличения времени операций можно уменьшить стоимость проекта.
Связь времени выполнения работы с вложением денежных средств определяется зависимостью
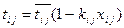, (2.8.1)
где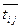 
– вероятностное время выполнения работы;
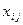– дополнительно вложенные средства;
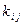– коэффициент пропорциональности зависимости времени от вложенных средств.
Критический путь также может быть функцией от объема вложенных средств. Если функция зависимости типа (2.8.1) является линейной, то подобная задача может быть решена симплекс-методом.
Задача 2.2.8.1. Задан сетевой график с указанием вероятностного времени выполнения работ,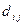 
– минимальное время работы 
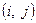. Оптимизировать проект путем вложения средств (на минимум времени выполнения операций). Сумма вложенных средств не должна превышать 10 денежных единиц. Заданы 
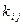– коэффициенты пропорциональности зависимости времени работы от вложенных средств.
 |
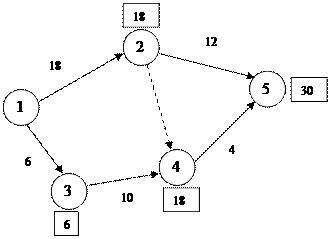Таблица 8.1
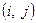
| (1, 2) | (1, 3) | (3, 4) | (2, 4) | (2, 5) | (4, 5) |
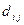
| 16 | 4 | 7 | 0 | 10 | 2 |
|
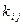
| 0,01 | 0,05 | 0,02 | 0 | 0,02 | 0,01 |
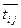
| 18 | 6 | 10 | 0 | 12 | 4 |
Решение.
1. Определяется критический путь путем простановки индексов по слоям от начала к концу и проходом обратно от конца к началу. Обратите внимание на индекс узла 4 – он получается за счет фиктивной работы.
2. Строится модель в общем виде. Неизвестные переменные: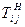 
– начало работы 
; 
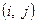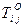– окончание работы ; 
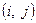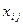– дополнительные денежные средства для работы 
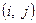. Минимизация времени выполнения проекта определяется временем выполнения события 5. Поэтому функция цели
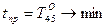. (2.8.2)
Ограничения на выделенные дополнительные ресурсы
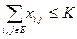, (2.8.3)
где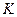 
– выделенные ресурсы в денежных единицах;
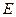– множество индексов сети.
Ограничения по минимальному времени выполнения работ
, 
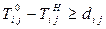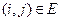(2.8.4)
Зависимость времени операций от вложенных средств
, 
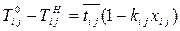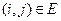. (2.8.5)
Ограничения по топологии сети (начало последующей работы не может быть ранее конца предыдущей работы)
, 
.
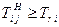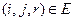3. Модель с числовыми данными имеет вид
,
; 
; 
;
; 
;
; 
;
; 
;
.
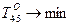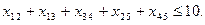
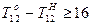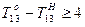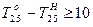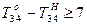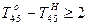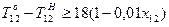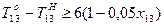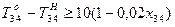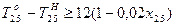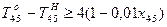Топология сети:
; 
; 
; 
; 
.
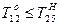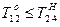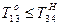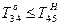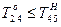После решения задачи симплекс-методом возможно сравнение критических путей исходной и оптимальной сети.
2.2.9 Сетевые графики. Вероятностная сеть.
Оценка времени выполнения работ
Сетевые графики проекта могут быть детерминированные или стохастические. Если характеристики операций включаются в сеть с некоторой вероятностью, то есть является стохастической.
С помощью экспертных оценок устанавливается минимальная продолжительность операции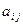 
(оптимистическая оценка), 
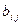– максимальная продолжительность (пессимистическая оценка) и наиболее вероятностная оценка 
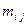(мода).
По функции распределения можно найти математическое ожидание и дисперсию времени выполнения операций.
В качестве типового распределения продолжительности операций обычно принимается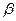 
– распределение с указанными оценками.
Для случая системы ПЕРТ сетевого планирования среднее значение определяется
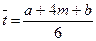. (2.9.1)
Дисперсия имеет вид
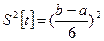. (2.9.2)
При двух оценках продолжительности математическое ожидание определяется по формуле
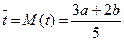. (2.9.3)
Дисперсия продолжительности операции
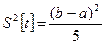. (2.9.4)
Длительность критического пути:
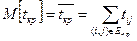, (2.9.5)
где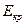 
– множество индексов операций для критического пути.
Дисперсия продолжительности критического пути считается как сумма дисперсий операций на критическом пути.
Если продолжительность работ отличается от среднего на малую величину и при этом критический путь не меняется, то можно считать, что продолжительность критического пути подчиняется нормальному закону распределения.
Вероятность того, что фактическая продолжительность критического пути меньше плановой
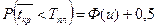, (2.9.6)
где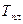 
– плановый срок выполнения работ;
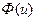– функция Лапласа;
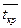– среднее время критического пути.
Функция Лапласа определяется по таблице, параметр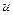 
рассчитывается по формуле
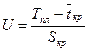. (2.9.7)
Здесь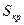 
– стандарт или квадратичное отклонение критического пути
.
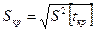Задача 2.2.9.1. Задан сетевой график с вероятностными оценками времени выполнения работ
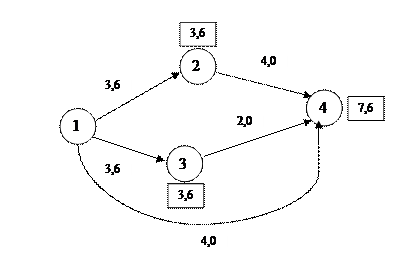
Таблица 9.1
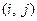
| Вероятностная оценка t | Оптимистическая оценка a | Пессимистическая оценка b | Дисперсия
|
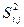
| (1,2) | 3,6 | 2,0 | 6,0 | 0,64 |
| (1,3) | 3,6 | 3,0 | 4,5 | 0,06 |
| (1,4) | 4,0 | 3,0 | 5,5 | 0,25 |
| (3,4) | 2,0 | 1,5 | 2,75 | 0,062 |
| (2,4) | 4,0 | 2,5 | 6,25 | 0,56 |
Определить вероятность выполнения проекта за 9 дней, за 12 дней.
Решение.
1. Вычисляются вероятностные оценки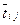 
по формуле
,
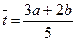результаты в табл. (9.1), а также дисперсия по формуле
.
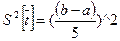2. По полученным характеристикам работ определяется критический путь (1, 2, 4).
Дисперсия критического пути
; 
.
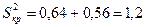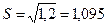3. Вычисление вероятности выполнения проекта за 9 дней
.
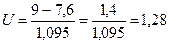По таблице значение функции Лапласа
.
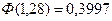Вероятность выполнения за 9 дней
.
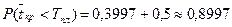4. Вычисление вероятности выполнения проекта за 12 дней
.
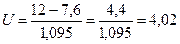Табличное значение функции Лапласа
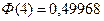, тогда вероятность
.
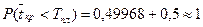2.2.10 Динамическое программирование.
Распределение ресурсов между предприятиями головной фирмы
Метод динамического программирования применяется к непрерывным и дискретным процессам оптимального управления.
Рассматривается многошаговый процесс с последнего шага. Чем кончился предпоследний шаг неизвестно, поэтому делается предположение о состоянии на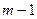 
шаге в различных вариантах, далее идут предположения о 
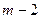шаге и т.д. Т.е. на каждом шаге выделяются условно-оптимальные варианты.
После достижения первого шага делается обратный проход для выбора оптимального варианта из условно–оптимальных.
В основе динамического программирования лежит принцип Беллмана:
«Каково бы ни было состояние системы в результате какого-то числа шагов, необходимо выбирать управление на ближайшем шаге так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах привело бы к максимальному выигрышу».
Функциональное уравнение для решения многоэтажного процесса Беллмана имеет вид
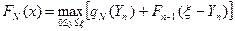, (2.10.1)
где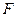 
– целевая функция процесса (доход, прибыль);
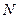– номер этапа процесса;
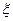– переменная состояния системы на 
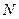-м этапе;
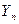– управляющая переменная, от выбора которой зависит результат на 
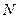-м этапе;
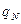– величина критерия, полученного на 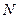-м этапе при выборе 
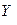от 0 до 
;
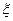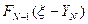– результирующее оптимальное значение критерия, достигаемое после прохождения 
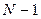этапа.
С помощью динамического программирования возможно решение задачи распределения ресурсов головной фирмой подчиненным предприятиям на расширение производства, так чтобы достигался глобальный оптимум, а не оптимум отдельных предприятий.
Задача 2.2.10.1. Фирме подчиняются 2 предприятия. Головная фирма распределяет ресурс в 150 тыс. денежных единиц для развития производства. Прирост прибыли по предприятиям определяется таблично, дискретность 30 денежных единиц.
Таблица 10.1
| Средства | Прирост прибыли по предприятиям | |
| №1 | №2 | |
| 30 | 11 | 14 |
| 60 | 20 | 26 |
| 90 | 32 | 30 |
| 120 | 44 | 60 |
| 150 | 65 | 70 |
Решение.
Общее функциональное уравнение Беллмана
.
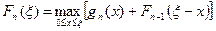Расчет можно проводить от первого предприятия ко второму или, наоборот, для данной задачи это несущественно. Осуществляется перебор вариантов для первого предприятия.
Условно-оптимальный план для первого предприятия:
Таблица 10.2
| Средства | Условно-оптимальный план | |
| 
| 
|
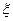
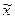
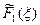
| 30 | 30 | 11 |
| 60 | 60 | 20 |
| 90 | 90 | 32 |
| 120 | 120 | 44 |
| 150 | 150 | 65 |
Для второго предприятия функция Беллмана имеет вид
.
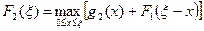Таблица 10.3
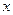
| 0 | 30 | 60 | 90 | 120 | 150 | Условно-оптимальный план | |
|
| 
| 
| ||||||
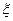
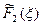
| 14 | 30 | |||||||
| 30 | 0+11 | 14+0 | ||||||
| 60 | 0+20 | 14+11 | 26+0 | 26 | 60 | |||
| 90 | 0+32 | 14+20 | 26+11 | 30+0 | 37 | 60 | ||
| 120 | 0+44 | 14+32 | 26+20 | 30+11 | 60+0 | 60 | 120 | |
| 150 | 0+65 | 14+44 | 26+32 | 30+20 | 60+11 | 70+0 | 71 | 120 |
Рассмотрим первую строку 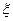=30. В первом столбце 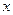=0,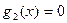 
, тогда 
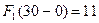по таблице (10.2). Во втором столбце 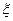=30, 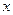=30, по таблице (10.1) 
; 
.
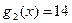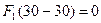Максимальное значение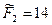 
, ему соответствует 
.
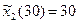Аналогично вычисляются остальные значения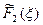 
и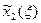 
.
Последнее значение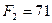 
и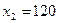 
является оптимальным для второго предприятия, 
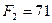является глобальным значением функции цели.
Оптимальный план 1-го предприятия можно определить:
.
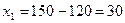Возможно также найти оптимальный план первого предприятия движением по таблицам от последней к первой. Значение 
получено от сложения 60+11, число 11 является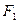 
по таблице (10.2), ему соответствует план 
.
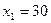2.2.11 Задачи раскроя материалов и составления смеси.
Область применения
Задачи раскроя материалов могут применяться в заготовительных цехах заводов при выборе варианта раскроя некоторого количества листов материала, так чтобы получить нужное количество заготовок деталей с минимальными затратами на раскрой.
Вначале составляются варианты раскроя. Каждый вариант определяет количество получаемых заготовок и величины отходов, которые можно также использовать в производстве.
Минимизируются издержки на раскрой материала и стоимость листов
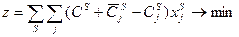, (2.11.1)
где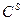 
– цена листа вида 
;
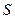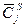– затраты на раскрой листа вида 
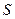при выборке 
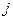-го варианта раскроя;
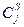– стоимость расходов при 
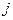-м варианте раскроя;
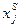– количество листов типа 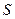, которое надо раскроить по варианту .
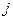Ограничение, связанное с выполнением плана производства
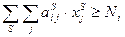, (2.11.2)
где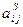 
– количество заготовок вида 
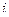, получаемых из листа типа 
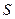при
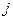-м варианте раскроя;
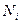– плановое задание по заготовкам.
Ограничение, связанное с запасами листов материалов на складах
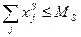. (2.11.3)
Ограничение на неотрицательность переменных
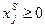. (2.11.4)
В качестве критериев может быть выбрана минимизация отходов или максимизация комплексов при комплектном формировании плана.
Задача 2.2.11.1. Из уголков в 4 м необходимо нарезать по 2 заготовки, которые входят в комплект в соотношении 3:8.
Варианты раскроя даны в таблице
Таблица 11.1
| Заготовки | Варианты раскроя уголка | ||
| 1 | 2 | 3 | |
| А | 2 | 0 | 1 |
| В | 1 | 6 | 5 |
Количество уголков на складе 100 шт. Организовать раскрой уголков на заготовки (построить модель и провести расчет количество уголков раскроя по каждому способу) из условия максимального числа комплектов.
Решение.
Модель в общем виде:
,
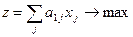где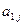 
– количество заготовок первого вида при раскрое по варианту 
;
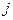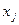– количество уголков, распределенных по 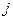-му варианту.
Количество комплектов определяет первый вид заготовок, т.к. входит в комплект в минимальном соотношении.
Ограничение по наличию уголков на складе
,
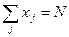где 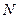– запас уголков.
Ограничение на ассортиментное соотношение в комплекте
.
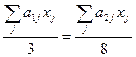Подробная числовая модель имеет вид
,
,
.
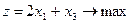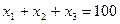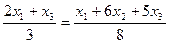Последнее уравнение преобразуется к виду
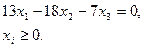
Канонический вид задачи линейного программирования
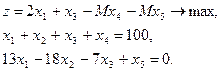
Применяем симплекс-метод последовательного улучшения. Здесь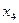 
и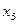 
искусственные переменные плана. Для использования 
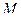-метода получения опорного плана. Для переменных 
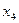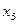, ввели оценки 
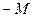, где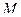 
– большое число.
Исходная симплексная таблица имеет вид
Таблица 11.2
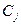
| 0 | 2 | 0 | 1 |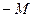 
| 
| ||
| № | 
| 
| 
| 
| 
| 
| 
| 
|
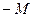
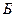
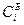
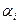
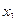
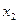
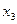
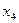
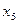
| 1 |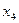
| 
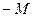
| 100 | 1 | 1 | 1 | 1 | 0 |
| 2 |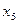
|
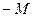
| 0 | 13 | –18 | –7 | 0 | 1 |
| 
| 
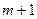
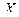
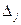
| 0 | –2 | 0 | –1 | ||
| 
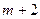
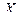
| –100 | –14 | 7 | 6 |
Столбец для ввода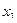 
в базис определен по 
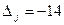в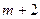 
строке, разрешающий элемент 13.
Следующая симплексная таблица, где в базис вводится 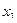, а из базиса выводится 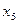примет вид после симплексного преобразования.
Таблица 11.3
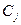
| 0 |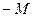
| 0 | 1 |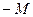 
| 2 | ||
| № |
| 
| 
| 
| 
|
| 
|
|
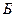
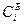
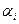
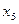
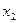
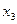
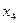
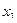
| 1 |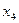 
| 
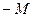
| 100 | –0,07 | 2,38 | 1,53 | 1 | 0 |
| 2 |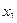 
| 2 | 0 | 0,07 | –1,38 | –0,53 | 0 | 1 |
|
|
| 
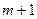
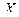
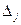
| 0 | 0,15 | –2,76 | 2,07 | ||
|
|
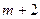
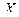
| –100 | 1,07 | –12,38 | –1,53 |
Разрешающий столбец определяется по элементу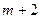 
строки равному 
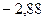. Разрешающая строка должна удалять искусственную переменную .
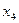Следующая симплексная таблица имеет вид при удалении столбца с 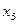в соответствии с 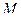-методом и заменой в базисе 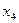на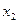 
.
Таблица 11.4
| № |
| 
|
| 
| 
| 
|
|
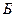
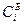
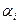
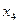
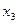
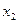
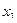
| 1 |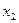 
| 0 | 42 | 0,42 | 0,64 | 1 | 0 |
| 2 |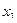
| 2 | 58 | 0,58 | 0,35 | 0 | 1 |
|
| 
|
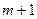
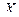
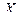
| 116 | 1,15 | -0,29 | ||
|
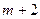
| 1 | 0 |
Столбец 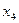из таблицы убирается, получается опорный план, он же является оптимальным поскольку 
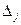в строке 
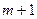положительны.
Еще раз С-М и в m+1 положительны.
Решение.
; 
; 
; 
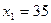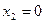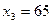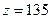, что соответствует числу заготовок первого вида.
Дата: 2018-12-28, просмотров: 330.
