Постановка транспортной задачи рассмотрена в разделе 2.2.12, модель транспортной задачи имеет вид
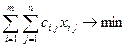 , (2.13.1)
, (2.13.1)
где 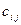 – стоимость перевозок продукта от
– стоимость перевозок продукта от 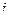 -го поставщика
-го поставщика 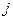 -му потребителю;
-му потребителю;
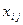 – неизвестный объем поставок продукта.
– неизвестный объем поставок продукта.
Ограничение по наличию продукта у поставщика
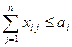 ,
, 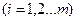 , (2.13.2)
, (2.13.2)
где 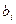 – запас продукта у
– запас продукта у 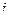 -го поставщика.
-го поставщика.
Ограничение на потребность продукта
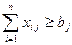 ,
, 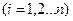 , (2.13.3)
, (2.13.3)
где 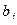 – потребность в продукте
– потребность в продукте 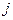 -го потребителя.
-го потребителя.
Условием разрешимости задачи является равенство общих ресурсов поставщиков общей потребности потребителей.
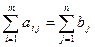 . (2.13.4)
. (2.13.4)
Если это равенство удовлетворяется, то задача называется закрытой, в противном случае задача открытая и для ее разрешимости необходимо вводить «фиктивного поставщика» или «фиктивного потребителя» с объемом продукта равным разности правой и левой части (2.13.4) получившей знак неравенства и нулевой стоимостью перевозок.
Задача 2.2.13.1. Три овощеводческих хозяйства имеют запасы картофеля в объемах 300 т, 1200 т, 720 т и заключили договора на поставку картофеля в г. Барнаул на склад 1100 т, на спиртзавод 420 т и на товарную станцию ж-д 800 т. стоимости перевозок 1 т в денежных единицах приведены в матрице
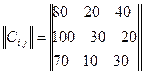 .
.
Здесь 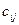 – стоимость перевозки от
– стоимость перевозки от 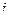 -го поставщика
-го поставщика 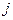 -му потребителю 1 т картофеля.
-му потребителю 1 т картофеля.
Определить объемы поставок от каждого поставщика каждому потребителю.
Решение.
Задача является открытой, поэтому, необходимо введение «фиктивного поставщика» №1 с объемом поставки 2320–2220=100 т.
Транспортная таблица имеет вид
Таблица 13.1
| Хозяйства | 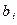
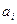
| Барнаул 1100 | Спиртзавод 420 | Ж-д станция 800 | 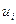
|
| №1 | 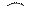 300 300
| 80 300 | 20 | 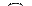 40 40
| 0 |
| №2 | 1200 |   100
700 100
700
| 50 |  20
500 20
500
| –20 |
| №3 | 720 |  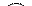 70 70
| 10 420 |  30
300 30
300
| –30 |
| Ф.П. | 100 | 0 100 | 0 | 0 | 80 |
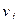
| 80 | –20 | 0 |
Методом наименьших элементов находим опорный план. Определяем потенциалы из равенств, положив 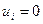 , составленных по базисным клеткам
, составленных по базисным клеткам
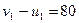 ;
; 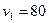 .
. 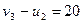 ;
; 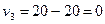 .
.
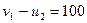 ;
; 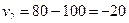 .
. 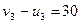 ;
; 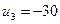 .
.
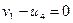 ;
; 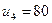 .
. 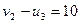 ;
; 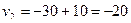 .
.
Проверка оптимальности плана по небазисным клеткам имеет результата
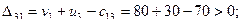 нет оптимума.
нет оптимума.
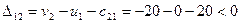 ;
;
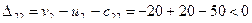 ;
;
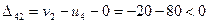 ;
;
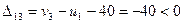 ;
;
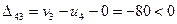 .
.
План не оптимален, в клетку (1, 3) необходимо ввести базисный объем перевозок в 300 единиц. Строится цикл перемещения этого объема. Новая транспортная таблица имеет вид.
Таблица 13.2
| Барнаул 1100 | Спиртзавод 420 | Ж–д станция 800 | 
| |
| №1 | 300 | 80 300 | 20 | 40 | –40 |
| №2 | 1200 | 100 400 | 50 | 20 800 | –60 |
| №3 | 720 | 70 300 | 10 420 | 30 | –30 |
| Ф.П. | 100 | 0 100 | 0 | 0 | 40 |
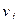
| 40 | –20 | –40 |
Новая система потенциалов начинается с клетки (2,3), поскольку она не перетерпела изменений.
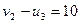 ;
; 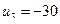 .
. 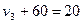 ;
; 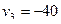 .
.
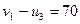 ;
; 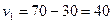 .
.
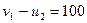 ;
; 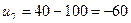 .
.
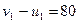 ;
; 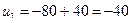 .
.
Проверка оптимальности оценками небазисных клеток
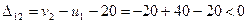 ;
;
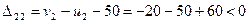 ;
;
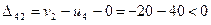 ;
;
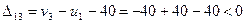 ;
;
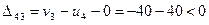 .
.
Получаем оптимальный план, оценки клеток отрицательны.
Решение в виде матрицы
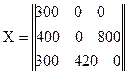 .
.
Потребитель «Барнаул» не получит 100 т.
2.2.14 Матричные игры.
Игры 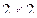 и
и 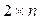
Теория игр рассматривает задачи, связанные с конфликтными ситуациями. Это задачи планирования боевых операций в военном деле, борьба торговых фирм, трестов, монополий в экономике капиталистических предприятий.
Игра называется с нулевой суммой, если один игрок выигрывает столько, сколько проигрывает другой.
Стратегия игрока это совокупность правил, определяющих действия игрока при каждом личном ходе игрока в зависимости от ситуации, сложившейся в процессе игры. Игра называется конечной, если у каждого игрока имеется конечное число стратегий.
Оптимальная стратегия - это стратегия, которая при многократном повторении игры обеспечивает игроку максимально возможный выигрыш (или минимальный средний проигрыш).
Рассматривается игра, где игрок 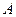 имеет
имеет 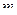 стратегий, а игрок
стратегий, а игрок 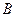 (противник) –
(противник) – 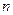 стратегий.
стратегий.
Личные ходы однозначно определяют игру, 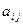 – исход игры, выигрыш
– исход игры, выигрыш 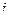 -го игрока при
-го игрока при 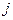 -м ходе противника.
-м ходе противника.
Если игра содержит кроме личных случайные ходы, то выигрыш при паре стратегий 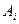 и
и 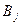 есть случайная величина и определяется математическим ожиданием.
есть случайная величина и определяется математическим ожиданием.
Значения 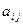 при выборе стратегий
при выборе стратегий 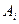 и
и 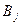 можно отразить матрицей
можно отразить матрицей
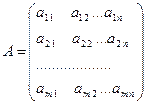 . (2.14.1)
. (2.14.1)
Антагонистическая игра, в которой каждый игрок имеет конечное множество стратегий называется матричной.
При задании платежной матрицы (2.14.1) игра называется 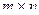 матричной игрой. Стратегии первого игрока
матричной игрой. Стратегии первого игрока 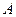 обозначаются номерами строк матрицы, стратегии второго игрока
обозначаются номерами строк матрицы, стратегии второго игрока 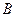 обозначаются номерами столбцов.
обозначаются номерами столбцов.
Если игрок 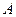 выбирает стратегию
выбирает стратегию 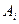 , то противник должен выбрать стратегию
, то противник должен выбрать стратегию 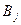 , для которого выигрыш первого игрока минимален.
, для которого выигрыш первого игрока минимален.
Найдем минимальное из чисел по строке 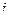 :
:
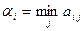 .
.
Выбирая стратегию 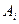 , игрок рассчитывает, что в результате действий противника выигрыш только
, игрок рассчитывает, что в результате действий противника выигрыш только 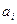 . Среди таких стратегий по строкам выбирается максимальный выигрыш
. Среди таких стратегий по строкам выбирается максимальный выигрыш
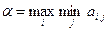 (2.14.2)
(2.14.2)
– это нижняя цена игры (максиминный выигрыш).
Стратегия 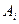 , которая дает такой выигрыш – максиминная стратегия.
, которая дает такой выигрыш – максиминная стратегия.
Аналогичные рассуждения для противника 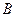 , заинтересованного в обращении в минимум выигрыша игрока
, заинтересованного в обращении в минимум выигрыша игрока 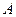 .
.
Максимальное значение выигрыша по столбцам
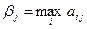 .
.
Из них минимальное значение
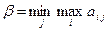 (2.14.3)
(2.14.3)
является верхней ценой игры (минимальный выигрыш).
Придерживаясь такой стратегии, игрок 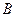 гарантирован, что он проиграет не больше
гарантирован, что он проиграет не больше 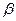 .
.
Существуют игры, в которых 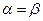 , это игра с седловой точкой, в ней существует такой элемент, который является минимальным в своей строке и максимальным в своем столбце
, это игра с седловой точкой, в ней существует такой элемент, который является минимальным в своей строке и максимальным в своем столбце
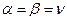 – чистая цена игры.
– чистая цена игры.
Седловой точке соответствуют две стратегии, они оптимальны и дают решение игры.
Чистая цена игры 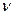 в игре с седловой точкой является значением выигрыша, которое игрок
в игре с седловой точкой является значением выигрыша, которое игрок 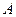 не может увеличить, а игрок
не может увеличить, а игрок 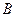 – уменьшить. В платежной матрице возможно несколько седловых точек.
– уменьшить. В платежной матрице возможно несколько седловых точек.
Возможно чередование чистых стратегий случайным образом, это смешанные стратегии.
Если стратегии 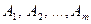 применяются с вероятностями соответственно
применяются с вероятностями соответственно 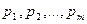 , то обозначили смешанную стратегию
, то обозначили смешанную стратегию
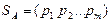 ,
,
причем 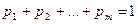 .
.
Аналогично для смешанной стратегии второго игрока
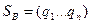 ,
,
где 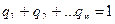 .
.
Решением игры будет пара смешанных стратегий 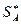 и
и 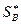 , так что если один из игроков придерживается своей оптимальной стратегии, то другому игроку невыгодно отступать от своей. Выигрыш – цена игры.
, так что если один из игроков придерживается своей оптимальной стратегии, то другому игроку невыгодно отступать от своей. Выигрыш – цена игры.
Основная теорема теории игр гласит, что каждая игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий. Цена игры лежит между нижней ценой 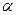 и верхней
и верхней 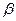 .
.
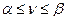 . (2.14.4)
. (2.14.4)
Наиболее простая игра 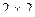 с платежной матрицей
с платежной матрицей
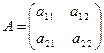 .
.
Игра может иметь седловую точку, тогда одна из стратегий может быть отброшена. Если седловой точки нет, т.е. 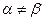 , то решение в смешанных стратегиях
, то решение в смешанных стратегиях 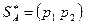 ;
; 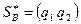 .
.
Решение может быть найдено из системы уравнений
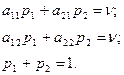 (2.14.5)
(2.14.5)
Решение системы (2.14.5) является
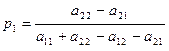 , (2.14.6)
, (2.14.6)
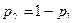 .
.
Цену игры можно найти подстановкой 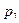 и
и 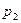 в одно из уравнений (2.14.5).
в одно из уравнений (2.14.5).
Аналогично находится стратегия противника 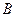
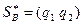
из уравнений
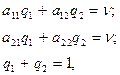 (2.14.7)
(2.14.7)
откуда решение
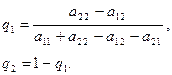 (2.14.8)
(2.14.8)
Игра 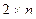 , где игрок
, где игрок 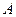 имеет 2 стратегии, а игрок
имеет 2 стратегии, а игрок 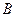 –
– 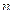 стратегий, может быть сведена к игре
стратегий, может быть сведена к игре 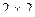 .
.
Строится графически ломаная линия – нижняя граница выигрыша, точка 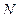 с максимальной ординатой соответствует цене игры, абсцисса этой точки соответствует вероятности
с максимальной ординатой соответствует цене игры, абсцисса этой точки соответствует вероятности 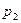 стратегии
стратегии 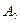 в оптимальной смешанной стратегии игрока
в оптимальной смешанной стратегии игрока 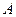 .
.
У игры 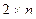 всегда имеется решение, в котором участвуют с каждой стороны 2 стратегии, которые являются активными. Если эти стратегии выделить, то игра
всегда имеется решение, в котором участвуют с каждой стороны 2 стратегии, которые являются активными. Если эти стратегии выделить, то игра 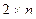 превращается в игру
превращается в игру 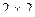 и решение можно найти по формулам (2.14.6) и (2.14.8).
и решение можно найти по формулам (2.14.6) и (2.14.8).
Задача 2.2.14.1. Найти решение игры, заданной матрицей
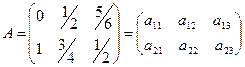 .
.
Решение .
1. Проверка на наличие седловой точки
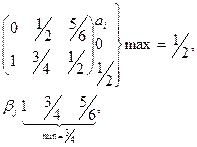
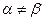 , седловая точка отсутствует.
, седловая точка отсутствует.
2. Графическое выделение активных стратегий.
На оси  откладываем отрезок [0, 1] и строим стратегии
откладываем отрезок [0, 1] и строим стратегии 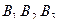 .
.

Активные стратегии 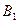 и
и 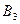 , им соответствует матрица
, им соответствует матрица
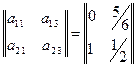 .
.
3. Решение игры по формулам (2.14.6)
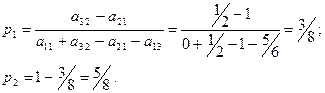
Определение цены игры по 1-му уравнению (2.14.5)
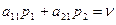 ;
;
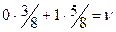 , откуда
, откуда 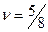 .
.
Для стратегии противника
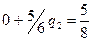 ; откуда
; откуда 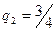 ;
; 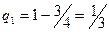 .
.
Получили стратегии
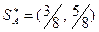 ;
; 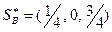 ;
;
и цена игры 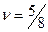 .
.
2.2.15 Матричные игры  и
и
линейное программирование
Основные понятия теории игр содержатся в разделе 2.2.14.
Стратегии игры двух игроков определяются платежной матрицей 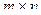 вида
вида
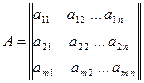 , (2.15.1)
, (2.15.1)
где 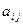 – выигрыш игрока
– выигрыш игрока 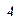 при
при 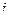 -ой стратегии, при стратегии
-ой стратегии, при стратегии 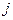 его противника.
его противника.
Определяются два оптимальных плана в смешанных стратегиях
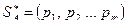 ;
; 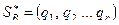 ,
,
где 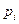 и
и 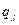 вероятности применения чистых стратегий игроками
вероятности применения чистых стратегий игроками 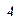 и
и 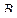 .
.
Неизвестна цена игры 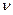 , стратегия
, стратегия 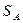 должна обеспечить выигрыш, не меньше чем
должна обеспечить выигрыш, не меньше чем 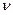 при любом поведении противника.
при любом поведении противника.
Чтобы цена была 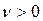 , надо чтобы элементы платежной матрицы
, надо чтобы элементы платежной матрицы 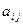 были неотрицательны. Это можно достигнуть, прибавив к элементам матрицы одну и ту же величину
были неотрицательны. Это можно достигнуть, прибавив к элементам матрицы одну и ту же величину 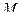 , при этом цена игры увеличится на
, при этом цена игры увеличится на 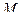 , но решение при этом не меняется.
, но решение при этом не меняется.
Предположим, что игрок 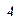 применяет оптимальную стратегию, средний выигрыш при применении противником
применяет оптимальную стратегию, средний выигрыш при применении противником 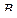 своей чистой стратегии
своей чистой стратегии 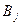
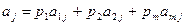 ,
, 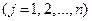 . (2.15.2)
. (2.15.2)
Стратегия оптимальная 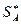 при любом поведении противника обеспечивает выигрыш не меньше чем
при любом поведении противника обеспечивает выигрыш не меньше чем 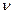 , отсюда условия
, отсюда условия
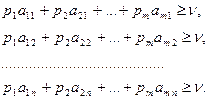 (2.15.3)
(2.15.3)
Разделим неравенства на 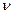 и обозначим
и обозначим
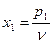 ,
, 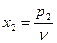 ,… ,
,… , 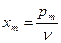 . (2.15.4)
. (2.15.4)
В результате получим ограничения
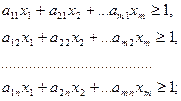 (2.15.4)
(2.15.4)
и так как 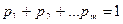 , то дополнительно
, то дополнительно
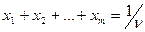 . (2.15.5)
. (2.15.5)
Поскольку выигрыш игрока 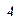 желателен максимальным, то
желателен максимальным, то 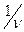 должна принимать минимальное значение, тогда функция цели примет вид
должна принимать минимальное значение, тогда функция цели примет вид
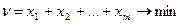 . (2.15.6)
. (2.15.6)
Задача (2.15.4), (2.15.6) является задачей линейного программирования. Для игрока 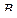 может быть построена двойственная задача минимизации выигрыша (проигрыша), т.е. максимизации
может быть построена двойственная задача минимизации выигрыша (проигрыша), т.е. максимизации 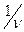 .
.
Обозначив
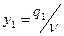 ;
; 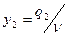 ; …
; … 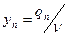 , (2.15.7)
, (2.15.7)
получим задачу
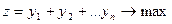 , (2.15.8)
, (2.15.8)
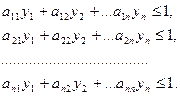 (2.15.9)
(2.15.9)
Задача 2.2.15.1. Сторона 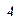 располагает тремя видами вооружения
располагает тремя видами вооружения 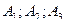 , сторона
, сторона 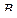 тремя видами помех
тремя видами помех 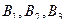 . Вероятность решения боевой задачи стороной
. Вероятность решения боевой задачи стороной 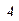 задана матрицей
задана матрицей
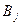
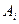
| 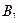
| 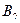
| 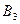
|
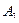
| 0,8 | 0,2 | 0,4 |
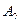
| 0,4 | 0,5 | 0,6 |
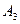
| 0,1 | 0,7 | 0,3 |
Сторона 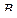 стремится воспрепятствовать боевой задачи. Найти решение задачи, т.е. вероятности
стремится воспрепятствовать боевой задачи. Найти решение задачи, т.е. вероятности 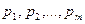 .
.
Решение.
Освободимся от дроби, для чего элементы матрицы умножим на 10
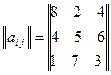 .
.
Цена игры получит значение 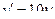 .
.
Задача для игрока  примет вид
примет вид
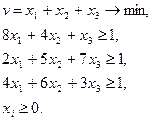
Для перехода к стандартной задаче линейного программирования возможна смена знаков, и применение симплекс-метода уточнения оценок (с допуском отрицательных элементов в столбце свободных членов).
Для использования метода последовательного улучшения плана можно рассмотреть двойственную задачу для игрока  .
.
Канонический вид ее приведен ниже с добавлением переменных  .
.
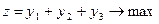 ,
,
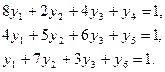
Исходная таблица имеет вид
Таблица 15.1
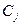
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| № | 
| 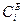
| 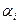
| 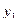
| 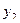
| 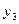
| 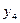
| 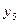
| 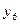
|
| 1 | 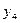
| 1 | 1 | 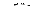
| 2 | 4 | 1 | 0 | 0 |
| 2 | 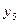
| 1 | 1 | 4 | 5 | 6 | 0 | 1 | 0 |
| 3 | 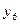
| 1 | 1 | 1 | 7 | 3 | 0 | 0 | 1 |
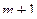
| 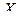
| 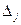
| 0 | –1 | –1 | –1 |
В качестве разрешающего столбца применим первый с разрешающим элементом 8, тогда 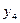 выводится из базиса и заменяется в базисе
выводится из базиса и заменяется в базисе 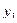 .
.
Таблица 15.2
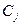
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| № | 
| 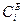
| 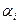
| 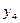
| 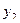
| 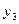
| 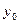
| 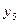
| 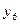
|
| 1 | 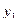
| 1 | 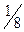
| 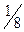
| 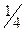
| 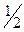
| 1 | 0 | 0 |
| 2 | 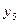
| 1 | 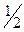
| – 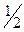 
| 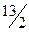
| 0 | 1 | 0 | |
| 3 | 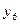
| 1 | 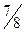
| – 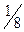
| 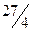
| 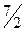
| 0 | 0 | 1 |
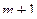
| 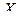
| 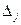
| 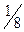
| 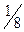
| – 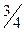
| – 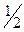
|
За разрешающий столбец принимаем при 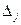 = –
= – 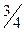 , в базис вводится
, в базис вводится 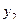 , из базиса выводится
, из базиса выводится 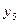 .
.
Новая симплексная таблица получит вид (15.3).
Таблица 15.3
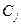
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| № | 
| 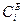
| 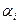
| 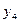
| 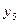
| 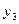
| 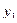
| 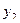
| 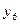
|
| 1 | 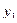
| 1 | 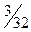
| 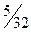
| – 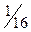
| 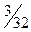
| 1 | 0 | 0 |
| 2 | 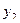
| 1 | 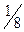
| – 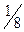
| 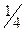
| 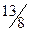
| 0 | 1 | 0 |
| 3 | 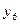
| 1 | 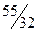
| 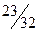
| – 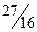
| 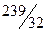
| 0 | 0 | 1 |
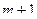
| 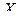
| 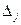
| 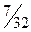
| 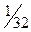
| 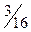
| 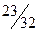
|
Поскольку все 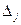 неотрицательны, получен оптимальный план
неотрицательны, получен оптимальный план
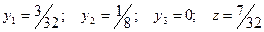 .
.
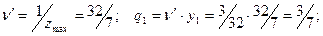
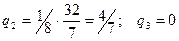 .
.
По значению 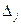 в последней таблице можно найти решение двойственной задачи
в последней таблице можно найти решение двойственной задачи
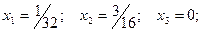
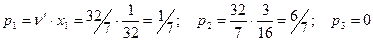 .
.
Дата: 2018-12-28, просмотров: 401.