Транспортной задачей называется разновидность задач линейного программирования.

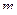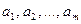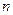Имеется  пунктов производства однородного продукта с объемами производства  и  пунктов потребления с объемами потребления 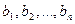. Известна стоимость перевозки единицы продукции от 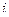-го пункта производства до 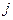-го пункта потребления 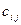. Требуется составить план перевозок так, чтобы запасы продукта у поставщиков были вывезены и удовлетворены потребности потребителей, при этом стоимость перевозки должна быть минимальной.

Модель имеет вид

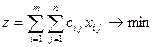,                                                   (2.12.1)

где 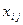 – объем перевозок от 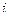-го поставщика 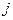-му потребителю.

Удовлетворение вывоза продукта:

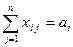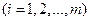, .                                           (2.12.2)

Удовлетворение потребности получателей продукта

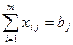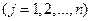, ,                                                     (2.12.3)

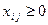.                                                                                       (2.12.4)

Условие разрешимости такой задачи:

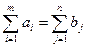,                                                                          (2.12.5)

т. е. суммарные запасы продукта равны суммарным объемам потребления. Такая задача называется закрытого типа. В противном случае задача открытого типа.

Для решения задачи при условии

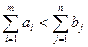                                                           (2.12.6)

вводится фиктивный 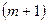 поставщик с запасом продукта

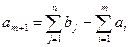.                                                           (2.12.7)

Если общий спрос продукта меньше суммарного запаса продукта

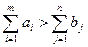,                                                                          (2.12.8)

то вводится фиктивный потребитель в 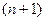 пункт потребления со спросом

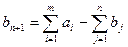.                                                             (2.12.9)

Тарифы на доставку продукта фиктивным поставщикам и потребителям назначаются нулевые.

Исходные данные и решение помещается в специальной транспортной таблице.

Планом называется матрица перевозок 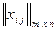. Для решения транспортной задачи вначале составляется опорный план, оценивается этот план на оптимальность, переходят к новому плану с меньшими транспортными затратами.

Опорный план возможно построить методом «северо-западного угла» и методом «минимального элемента».

При методе «минимального элемента» первой загружается клетка с наименьшим тарифом. Далее загружается клетка той же строки (столбца) со следующим по величине тарифом и т.д.

Метод «наименьшего элемента» дает план, более близкий к оптимальному, по сравнению с методом «северо-западного угла».

Задача 2.2.12.1. В резерве железнодорожных станци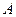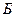й ,  и 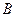 находятся 100, 150 и 50 порожних вагонов, пригодных для перевозки сырья. Зерно находится в 4 пунктах с потребностью вагонов 75, 80, 60 и 85 для перевозки зерна. Стоимость перегона одного вагона от станции до пунктов отражены в таблице.

Составить экономическую модель транспортной задачи из условия минимизации стоимости перегона вагонов. Найти решение методом потенциалов.

Таблица 12.1

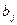
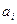
	75	80	60	85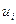
100	6	7 5	3 60	5 35	0
150	1 75	2 75	5	6	5
50	3	10	20	1 50	6
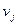
	6	7	3	5

Решение.

Задача является закрытой, т.к. выполняется

.

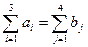Для построения опорного плана применен метод «минимального элемента».

Вычисление потенциалов по базисным клеткам

;

; ;                                                ; ;

; ;                                  ; ;

; ;                                     ; .

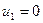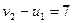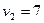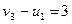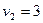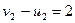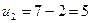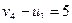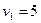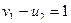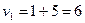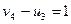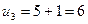Проверка на оптимальность небазисных клеток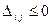

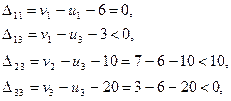
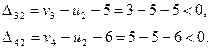
Оценки оптимальности удовлетворяют, план оптимален, перераспределения базиса не требуется.

План отражен в матрице

.

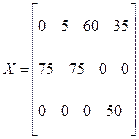Общая стоимость перевозок

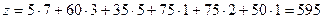 денежных единиц.