На отдельных предприятиях принято покомплектное планирование выпуска продукции. В случае комплектной поставки продукции задача составления годовой производственной программы имеет ассортиментную постановку. В случае известной производительности технологических линий в качестве неизвестного выбирается доля рабочего времени, отведенная на изготовление данного вида продукции в плановом периоде.
Обозначим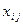 
– долю рабочего времени 
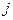-ой технологической линии, отведенную под изготовление изделия 
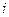. Предполагается, что на технологических линиях могут изготавливаться все виды изделий.
Тогда сумма всех долей рабочего времени по каждой технологической линии
, 
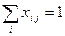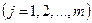. (2.5.1)
Количество изделий вида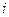 
, произведенных на всех технологических линиях, определяется
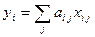, (2.5.2)
где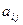 
– производительности 
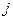-ой технологической линии по 
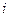-му изделию.
Пусть задано ассортиментное соотношение изделий, входящих в комплект
.
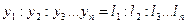Комплект определяет минимальный набор изделий. Тогда условие максимизации количества комплектов
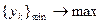(2.5.3)
и соотношение комплектности
, 
.
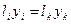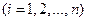Комплекты могут быть разных видов.
Ассортиментный набор определяет комплектный выпуск продукции предприятия (машино–комплект).
Возможен суточный комплект – количество деталей и узлов, необходимых для работы сборочного цеха в течение суток.
Групповой комплект – объединение деталей и узлов в комплект по признаку одинакового срока подачи на сборку. Условный комплект – выбор из набора изделий типового, условного изделия, вся остальная продукция предприятия планируется в виде условных деталей и узлов по выбранному изделию.
Задача 2.2.5.1. Выпускаются изделия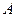 
, 
, 
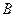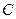в ассортиментном соотношении 2:1:3, что составляет комплект.
Таблица 5.1
| № технологической линии | Месячная производительность (тыс. шт.) | ||
|
|
| 
| |
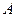
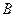
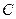
| 1 | 200 | 200 | 400 |
| 2 | 600 | 400 | 900 |
| 3 | 300 | 200 | 700 |
Составить модель оптимальной загрузки технологических линий из условия максимума производства комплектов.
Поскольку задана производительность технологических линий, то неизвестная переменная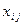 
– доля планового периода, отведенная под 
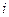-е изделие на 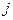-ой технологической линии, а также 
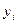– количество 
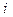-х изделий, получаемым по всем технологическим линиям.
В ассортиментном соотношении минимальным является для второго изделия, оно определяет комплект.
Тогда функция цели:
.
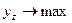Ограничения по плановому периоду
, 
.
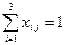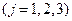Общий объем выпуска изделий
, 
.
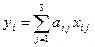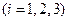Соотношение изделий, определяющих комплект:
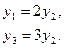
Далее необходимо составить модель в числовых данных.
2.2.6 Математическая обработка результатов опытов в планировании эксперимента. Полный факторный эксперимент.
Свойства матрицы планирования
Полный факторный эксперимент проводится тогда, когда по времени и затратам небольшие издержки.
Строится матрица планирования в кодированном виде путем перебора значений каждого фактора, сочетаний всех уровней, что соответствует полному факторному эксперименту.
Число опытов
,
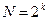где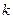 
– число факторов,
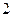– число уровней.
Матрица планирования эксперимента обладает в этом случае свойствами:
1. Свойство симметричности – алгебраическая сумма элементов каждого столбца матрицы равна нулю.
2. Условие нормировки – сумма квадратов элементов каждого столбца равна числу опытов.
3. Свойство ортогональности – сумма почленных произведений двух вектор – столбцов матрицы равна нулю.
4. Свойство ротатабельности – точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра и не зависит от направления.
После произведения эксперимента строится модель, т.е. по результатам опытов определяются коэффициенты выбранной регрессионной модели методом наименьших квадратов. Далее проверяется однородность дисперсии по строкам матрицы планирования и адекватность модели.
Задача 2.2.6.1. Рассматривается полный факторный эксперимент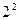 
. По матрице планирования в кодированном виде и результатах опытов построить регрессионную модель и проверить адекватность модели. Проверить также однородность дисперсии повторных измерений.
Таблица 6.1
| № | 
| 
| 
|
| 
| |
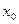
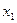
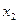
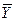
| 1 | +1 | –1 | –1 | 7,2 | 7,0 | 7,1 |
| 2 | +1 | –1 | +1 | 9,5 | 9,3 | 9,4 |
| 3 | +1 | +1 | –1 | 6,4 | 6,6 | 6,5 |
| 4 | +1 | +1 | +1 | 9,1 | 9,26 | 9,18 |
Выбирается двухфакторная линейная модель
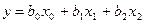. (2.6.1)
Определяются средние значения повторных измерений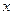 
.
Коэффициенты уравнения регрессии определяются как среднее произведение столбца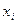 
на 
.
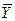Так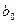 
определяется:
;
; 
.
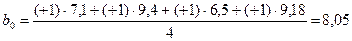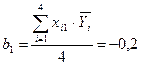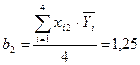Уравнение регрессии примет вид
.
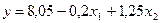Для проверки однородности дисперсии по строкам матрицы получим значения дисперсии
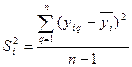, (2.6.2)
где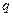 
– номер повторного измерения;
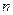– количество повторных измерений.
;
;
.
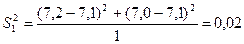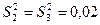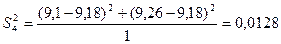Общая дисперсия
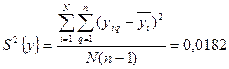. (2.6.3)
Для проверки однородности дисперсии применяется критерий Фишера.
Экспериментальный критерий
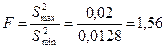. (2.6.4)
Табличный критерий Фишера при степенях свободы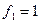 
и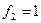 
при уровне значимости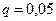 
.
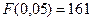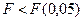, следовательно, дисперсия однородна.
Для проверки адекватности модели определяется остаточная сумма квадратов.
Таблица 6.2
| № | 
| 
| 
| 
|
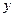
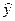
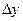
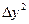
| 1 | 7,1 | 7,0 | 0,1 | 0,01 |
| 2 | 9,4 | 9,5 | 0,1 | 0,01 |
| 3 | 6,5 | 6,6 | 0,1 | 0,01 |
| 4 | 9,2 | 9,1 | 0,1 | 0,01 |
|
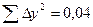
Здесь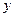 
– значение параметра оптимизации, полученное опытом, 
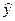– значение параметра, вычисленного по уравнению регрессии.
Остаточная дисперсия
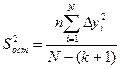. (2.6.5)
.
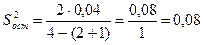Экспериментальный критерий Фишера
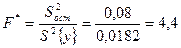. (2.6.6)
Для определения табличного критерия
Степени свободы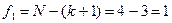 
; 
.
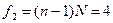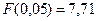
Т.к. экспериментальный критерий меньше табличного, то модель адекватна.
2.2.7 Управление запасами материалов. Типы моделей.
Простейшая модель Уилсона
На основании составленной производственной программы рассчитывается потребность в материалах для ее выполнения по существующим нормативам. Далее организуется управление запасами материалов.
Запасы могут быть:
- текущие, между двумя очередными поставками материалов;
- страховые, для обеспечения бесперебойного процесса производства в случае нарушения снабжения;
- сезонные, для обеспечения материалами при сезонных изменениях работы транспорта.
Большие запасы материалов дают возможность удовлетворить изменения в потребности материалов, но вызывают большие издержки хранения. Малые запасы сокращают расходы на хранение, но не дают гарантий срыва работы производства при нарушении снабжения.
Модели управления запасами зависят от вида спроса, вида поставок и объема поставок.
Спрос на материалы зависит от характера производства и может быть:
- стационарный и нестационарный;
- детерминированный или стохастический;
- непрерывно-распределенный или дискретный.
Поставки материалов зависят от расположения поставщиков и организации их и могут быть:
- мгновенные;
- с задержкой на фиксированный срок;
- с задержкой на случайный интервал времени с некоторым вероятностным законом распределения.
Объемы поставок могут быть:
- фиксированной величины;
- случайной величины.
Каждый указанный фактор определяет тип модели, поэтому при составлении модели необходимо изучить тип конкретного производства и особенности поставщиков.
В качестве критериев в оптимизационной модели могут быть:
- издержки хранения материалов;
- транспортные расходы;
- затраты на штрафы от сбоя производства.
Простейшая модель ставится для производства, где дневной расход материалов постоянный, доставка производится мгновенно, во внимание принимаются только издержки на хранение и заказы материалов.
Объем заказов определяется
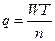, (2.7.1)
где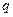 
– объем материала на один заказ;
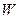– дневной расход материалов;
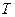– число дней в плановом периоде;
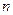– количество заказов за время 
.
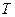Ищется наилучший размер заказа, обеспечивающий бесперебойную работу производства и дающий минимум издержек на хранение.
Уилсоном получена следующая формула для количества заказов за плановый период
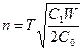, (2.7.2)
где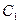 
– стоимость хранения единицы материала в сутки;
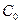– накладные расходы на одну партию, не зависящие от объема поставок.
Задачи управления запасами могут быть сформулированы также в терминах теории массового обслуживания.
Задача 2.2.7.1. Дневной расход материала 500 единиц, производство конвейерное. Поставщик находится в том же городе, где расположено предприятие. Составить модель политики управления запасами (объем материала на 1 заказ и количество заказов на квартал), взяв за критерий минимум издержек на заказы и хранение материалов.
Накладные расходы на одну партию 5 ден. ед., стоимость хранения единицы материала 7 денежных единиц.
Указания. Использовать формулу Уилсона. Как выводится эта формула?
Дата: 2018-12-28, просмотров: 338.
