Стандартная задача линейного программирования в векторной форме имеет вид
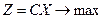, (2.2.1)
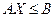, (2.2.2)
.
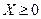В развернутой форме
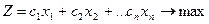, (2.2.3)
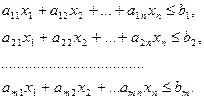(2.2.4)
Подобные задачи применяются в составлении производственной программы предприятия, ограничения можно отнести к расходу ресурсов, функция цели содержит стоимость продукции или прибыль.
Для подобной задачи можно составить двойственную
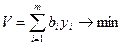. (2.2.5)
, 
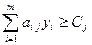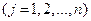(2.2.6)
.
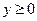Такая задача интерпретируется как задача минимизации стоимости ресурсов. Здесь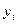 
выступает как «теневая цена» ресурса, т.е. цена ресурса для технологии данного предприятия. Л.В. Канторовичем они названы «объективно-обусловленными оценками» («ООО»).
Задача 2.2.2.1. Для изготовления 3 видов продукции используется 2 виды сырья. Составить модель расчета плана, рассчитать оптимальный план из условия максимизации прибыли. Получить решение двойственной задачи.
Таблица 2.1
| Сырье | Нормы расхода в кг на единицу продукции | Запасы сырья на складах | ||
| 
| 
| ||
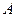
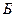
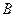
| 1 | 1 | 3 | 5 | 9 |
| 2 | 2 | 2 | 1 | 5 |
| Прибыль от продукции | 3 | 1 | 2 | |
Решение.
Предлагается решение симплекс-методом последовательного улучшения плана.
Модель имеет вид
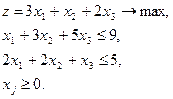
Канонический вид задачи для ограничений
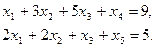
Последовательность симплекс таблиц приводится ниже.
Опорная таблица:
Таблица 2.2
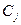
| 3 | 1 | 2 | 0 | 0 | |||
| Базис | Ресурсы | |||||||
| № |
| 
| 
| 
| 
| 
| 
| 
|
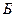
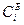
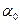
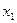
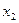
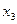
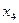
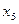
| 1 |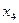
| 0 | 9 | 1 | 3 | 5 | 1 | 0 |
| 2 |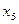 
| 0 | 5 | 2 | 2 | 1 | 0 | 1 |
| 
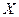
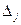
| 0 | –3 | –1 | –2 | 0 | 0 |
Симплекс-преобразование в методе последовательного улучшения плана имеет вид
,
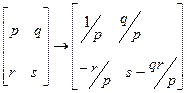где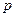 
– разрешающий элемент;
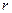– элемент разрешающего столбца;
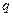– элемент разрешающей строки;
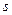– произвольный элемент.
После ввода в базисе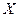 
, получим
Таблица 2.3
|
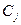
| 0 | 1 | 2 | 0 | 3 | |||
| № |
| 
|
| 
| 
|
| 
| 
|
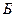
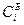
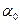
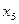
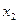
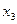
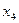
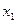
| 1 |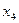
| 0 | 13/2 | –1/2 | 2 | 9/2 | 1 | 0 |
| 2 |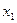 
| 3 | 5/2 | 1/2 | 1 | 1/2 | 0 | 1 |
|
|
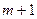
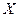
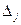
| 15/2 | 3/2 | 2 | –1/2 |
В базисе далее заменяется 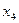на
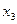
Таблица 2.4
|
| ||||||||
| № |
|
|
|
|
|
| 
| 
|
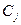
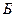
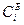
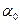
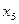
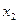
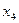
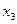
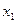
| 1 |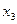
| 2 | 13/9 | –1/9 | 4/9 | 2/9 | 1 | 0 |
| 2 |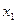 
| 3 | 16/9 | 5/9 | 7/9 | –1/9 | 0 | 1 |
|
|
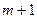
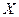
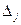
| 74/9 | 13/9 | 20/9 | 1/9 |
Получили оптимальный план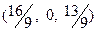 
; 
.
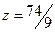По данной таблице можно найти решение двойственной задачи (в колонке векторов 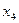и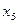 
)
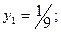
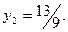
2.2.3 Производственная функция Кобба-Дугласа.
Коэффициенты эластичности
Функция Кобба–Дугласа применяется для прогнозирования объемов производства, она связывает выпуск продукции и затраты.
Функция имеет вид
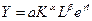, (2.3.1)
где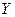 
– объем производства;
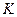– индекс производственных фондов (основные капиталовложения);
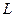– индекс труда (рабочая сила в сфере материального производства);
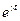– фактор, связанный с техническим прогрессом.
Важный экономический показатель для производственной функции является коэффициент эластичности
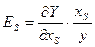, (2.3.2)
где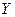 
– объем производства;
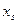– затраты 
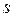-го фактора для производства продукции.
Коэффициент эластичности безразмерен, показывает на сколько процентов изменяется выпуск продукции при изменении на 1% интенсивности затрат соответствующего фактора.
Функция является нелинейной многофакторной регрессионной моделью.
Можно показать, что коэффициенты регресси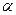и 
и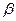 
являются коэффициентами эластичности по капиталам и труду.
Задача 2.2.3.1. В таблице приведены данные по объемам выпуска продукции 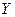, затрат капитала 
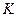и труда 
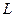в некоторой отрасли за 10 лет.
Таблица 3.1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | |
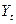
| 50,0 | 58,0 | 37,0 | 110,0 | 130,0 | 120,0 | 150,0 | 146,5 | 310,0 |
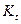
| 2 | 5,2 | 2 | 6,6 | 2,5 | 10,4 | 5,6 | 10,4 | 13,0 |
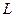
| 2 | 2 | 2 | 4 | 6 | 2 | 6 | 6 | 6 |
Указания:
Использовать функцию Кобба–Дугласа в виде
.
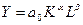Для определения коэффициентов регресси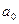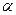и 
, и 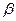с помощью логарифмирования перейти к линейной модели.
С помощью метода МНК (см. 2.2.1) построить систему нормальных уравнений и решить ее относительно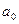 
, 
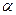и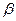 
.
Дата: 2018-12-28, просмотров: 248.
