Метод позволяет свести решение нелинейных уравнений к решению последовательности линейных задач. Метод быстро сходится. Однако этот метод эффективен при весьма жестких ограничениях на характер функций 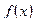 :
:
1. существование второй производной функции 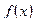 на множестве
на множестве 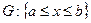 ;
;
2. удовлетворения первой производной условию 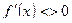 для всех
для всех  принадлежащих
принадлежащих 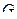 ;
;
3. знакопостоянство 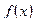 ,
, 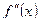 и
и 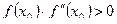 для всех
для всех  , принадлежащих
, принадлежащих 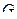 .
.
Пусть действительный корень уравнения 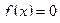 отделен на отрезке
отделен на отрезке 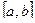 . Возьмем на отрезке
. Возьмем на отрезке 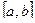 такое число
такое число 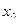 , при котором
, при котором 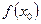 имеет тот же знак, что и
имеет тот же знак, что и 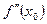
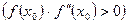 .
.
Итерационная последовательность строится:
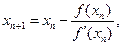
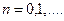 (2.16.1)
(2.16.1)
Предполагается, что 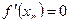 .
.
Методика решения нелинейных уравнений методом Ньютона
1. Задать начальные приближения 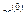 так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство 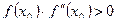 , а также малое положительное число
, а также малое положительное число  . Положить
. Положить 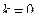 .
.
2. Вычислить 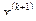 по методу Ньютона:
по методу Ньютона: 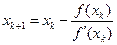 .
.
3. Процесс завершить если 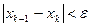 тогда корень
тогда корень 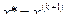 , иначе
, иначе 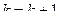 и перейти к пункту 2.
и перейти к пункту 2.
Пример 2.2.16.5. Методом Ньютона найти положительный корень уравнения 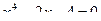 с точностью до 0,001. Положительный корень заключен в промежутке
с точностью до 0,001. Положительный корень заключен в промежутке 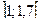 , так как
, так как 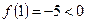 , а
, а 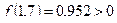 .
.
Решение.
Здесь 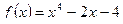 ,
,
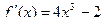 ,
,
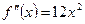 .
.
Так как 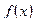 и
и 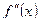 при
при 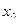 =1,7 имеют один и тот же знак, а именно
=1,7 имеют один и тот же знак, а именно 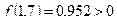 и
и 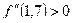 , тогда
, тогда
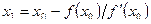 , где
, где 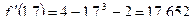 ,
,
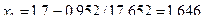 .
.
Проверить условие завершения процесса итераций:
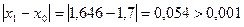 .
.
Применим снова метод Ньютона.
Имеем 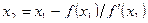 , где
, где 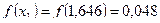 ,
, 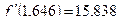 ; значит,
; значит, 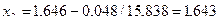 .
.
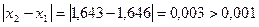 .
.
Аналогичным образом находим 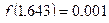 ;
; 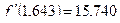 ,
, 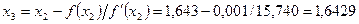 .
.
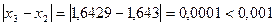 .
.
Следовательно, искомый корень с точностью до 0,001 равен 1,6429.
Метод итераций
Если данное уравнение 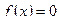 приведено к виду
приведено к виду 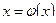 , где
, где 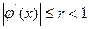 всюду на отрезке
всюду на отрезке 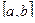 , на котором исходное уравнение имеет единственный корень, то исходя из некоторого начального значения
, на котором исходное уравнение имеет единственный корень, то исходя из некоторого начального значения 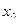 , принадлежащего отрезку
, принадлежащего отрезку 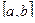 , можно построить такую последовательность:
, можно построить такую последовательность:
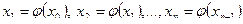 .
.
Пределом этой последовательности является единственный корень уравнения 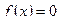 на отрезке
на отрезке 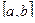 .
.
Методика решения нелинейных уравнений методом простой итерации
1. Уравнение f( x)=0 привести к каноническому виду 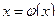 . Задать начальное приближение
. Задать начальное приближение 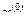 ,
, 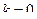 ,
, 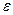 – погрешность. Для сходимости нужно обеспечить выполнение условия
– погрешность. Для сходимости нужно обеспечить выполнение условия 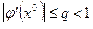 ,
, 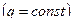 .
.
2. Вычислить следующее приближение по методу простой итерации:
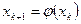
3. Итерационный процесс завершаются если 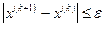 , тогда
, тогда 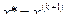 ,
,
иначе 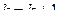 и перейти к 2.
и перейти к 2.
Пример 2.2.16.6. Методом итераций найти приближенное значение корня уравнения 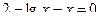 с точностью до 0,001, корень уравнения отделен на отрезке
с точностью до 0,001, корень уравнения отделен на отрезке 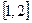 .
.
Решение.
Запишем исходное уравнение в виде 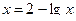 .
.
Здесь 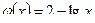 ,
, 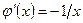 , то
, то 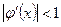 в промежутке
в промежутке 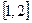 и поэтому метод итераций применим при начальном приближении
и поэтому метод итераций применим при начальном приближении 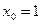 . Найдем теперь первое приближенное значение:
. Найдем теперь первое приближенное значение:
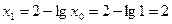 .
.
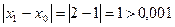 .
.
Найдем второе и последующие приближения:
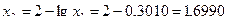 ;
;
Проверим погрешность
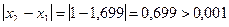 ;
;
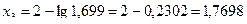 ;
;
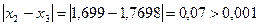 ;
;
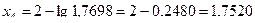 ;
;
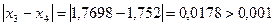 ;
;
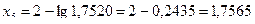 ;
;
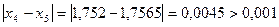 ;
;
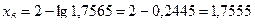 ;
;
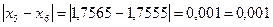 ;
;
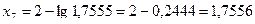 .
.
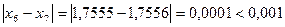 ;
;
Таким образом, искомый корень 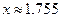 .
.
Дата: 2018-12-28, просмотров: 454.