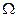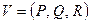Пусть дана область  в пространстве , и  – векторное поле.

Определение. Векторное поле называется потенциальным в области 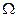, если существует функция  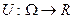такая, что

, , ,

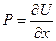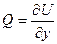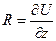при этом 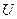 называют потенциалом векторного поля .

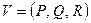Теорема (характеризация потенциальных полей). Рассмотрим векторное поле в некоторой области . Следующие три условия эквивалентны:

1) Поле 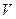потенциально.

2) Интеграл от поля 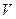 вдоль ориентированной кривой не зависит от начальной и конечной точек этой кривой.

3) Интеграл от векторного поля по любой замкнутой кривой равен нулю.

Пример 2.1.12.1. Показать, что поле 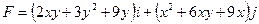 является потенциальным, и найти потенциал этого поля.

Решение.

Данное векторное поле определено на всей плоскости 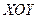, являющейся односвязной областью. Покажем, что 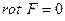, т.е. что поле безвихревое, а следовательно, и потенциальное. Действительно, так как

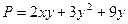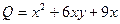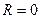, , , то

.

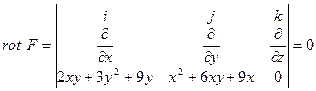Потенциал 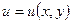 вычислим по формуле

,

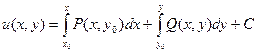т.е. .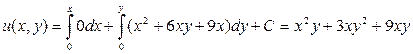

Здесь в качестве начальной точки взята точка .

Формула Грина

Теорема (формула Грина). Пусть в области 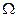 задано гладкое векторное поле 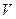, также задано множество  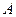в 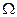 с кусочно-гладкой границей, которая правильно ориентирована, тогда справедлива следующая формула:

,

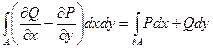где ,  – координаты векторного поля.

Пример 2.1.13.1. Применяя формулу Грина, вычислить

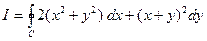, если  – контур треугольника с вершинами 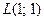, , 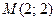, 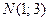пробегаемый против хода часовой стрелки. Проверить результат непосредственным интегрированием.

Решение.

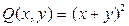, . Находим . Таким образом,

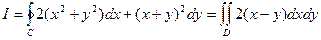, где область  – треугольник 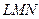. Уравнение прямой , уравнение 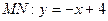. Вычислим двойной интеграл по данной области:

.

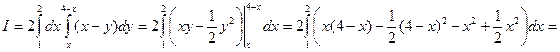
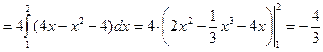Вычислим теперь непосредственно криволинейный интеграл по контуру , состоящему из звеньев , , :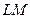

.

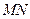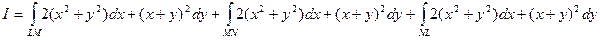Уравнение 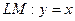; следовательно , .

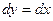Уравнение 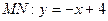; следовательно , .

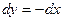Уравнение 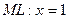; значит , .

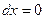Таким образом,

.

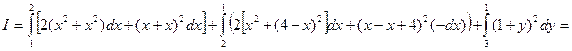
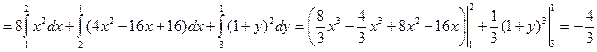Пример 2.1.13.2. Применяя формулу Грина, вычислить 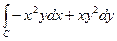, где  – окружность 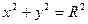, пробегая против хода часовой стрелки.

Решение.

Здесь , . Тогда 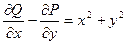. Следовательно,

.

Формула Гаусса–Остроградского

Поверхностные интегралы

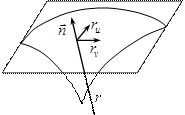Рассмотрим открытое множество , точки которого будем обозначать 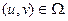. Пусть  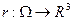– дифференцируемая функция, .

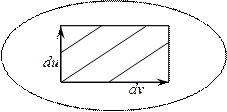Образ отображения  представляет собой при некоторых дополнительных предположениях двухмерную поверхность в .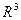

Рассмотрим векторы

;

.

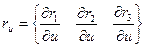Они будут касательными к поверхности в текущей точке.

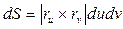Потребуем, чтобы матрица, состоящая из векторов  и , имела ранг 2. Тогда  – элемент площади поверхности,  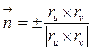– единичные нормали в текущей точке поверхности.

Определение. Поверхность ориентируема, если в каждой точке поверхности можно определить нормаль так, чтобы нормали непрерывно изменялись от точки к точке. Такую поверхность также называют двухсторонней.