Пусть 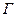 – кривая, описываемая в декартовой системе координат на плоскости непрерывной неотрицательной функцией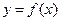 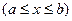, имеющей на  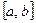непрерывную производную. Рассмотрим формулу для вычисления  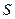– площади поверхности вращения кривой  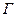вокруг оси  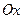в трехмерном пространстве.

Теорема. Для величины 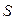 справедлива следующая формула:

.

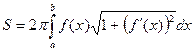Пример 2.1.7.1. Найти площадь поверхности «веретена», которое получается в результате вращения одной полуволны синусоиды 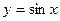 вокруг оси .

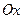Решение.

.

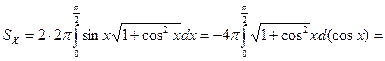
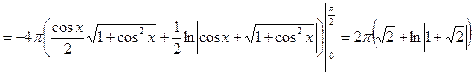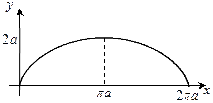Пример 2.1.7.2. Найти площадь поверхности,

образованной вращением одной арки циклоиды

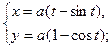 вокруг оси .

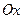Решение.

Поскольку арка циклоиды симметрична относительно прямой 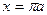, рассчитаем половину площади поверхности в пределах 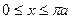, что соответствует .

.

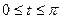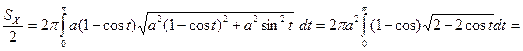
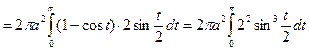Выполним замену 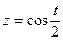, тогда , .

.

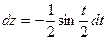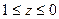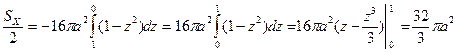Вся площадь поверхности составляет .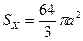

Пример 2.1.7.3. Найти площадь поверхности, образованной вращением кардиоиды 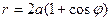 вокруг полярной оси.

Решение.

;

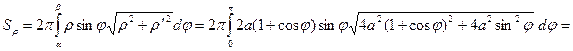
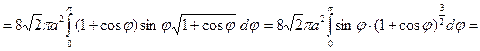
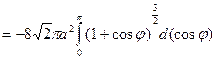Выполним замену 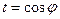, тогда, .

.

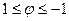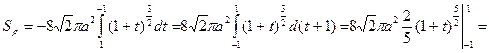
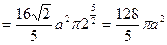Понятие компакта

Компакты

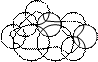Определение. Множество  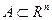называется компактным множеством (компактом), если из любой последовательности точек этого множества можно извлечь подпоследовательность, сходящуюся к некоторой точке множества .

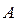Теорема (критерий компактности). Множество 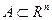 является компактом тогда и только тогда, когда оно замкнуто и ограничено.

Определение. Пусть нам дан набор множеств 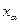,  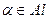(  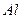называется индексным множеством). Совокупность индексированных множеств  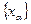называется семейством.

Определение. Пусть дано множество 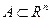 и семейство множеств 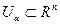. Семейство множеств  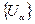называется покрытием множества 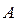, если  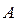содержится в объединении всех множеств рассматриваемого семейства .

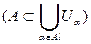Определение. Говорят, что 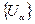 – открытое покрытие множества 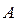, если:

1. 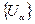 – покрытие ,

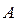2. каждое 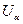 – открытое множество.

Определение. Покрытие 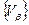 называется подпокрытием покрытия 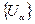, если любой элемент покрытия  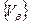является элементом покрытия 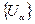, то есть для всех  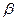существует такое 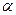, что .

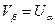Теорема Бореля. Множество 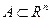 – компакт тогда и только тогда, когда из любого открытого покрытия множества  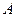можно извлечь конечное подпокрытие.

Пример 2.1.8.1. Показать, что отрезок 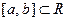 является компактным множеством в этом пространстве.

Решение.

Поскольку отрезок 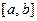 является ограниченным множеством, следовательно, из любой последовательности его элементов можно извлечь подпоследовательность, которая имеет конечный предел (теорема Больцано-Вейерштрасса). В силу теоремы о предельном переходе в неравенстве (см. [17] гл. 2 теорема 1.3), предел такой последовательности принадлежит отрезку 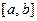. Таким образом, по определению промежуток  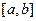является компактным множеством.