СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 5
1 ПРОГРАММА ГОСУДАРСТВЕННЫХ ЭКЗАМЕНОВ. 6
2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВОПРОСАМ ПРОГРАММЫ.. 8
2.1 Математический анализ 8
2.1.1 Теоремы Вейерштрасса. 8
2.1.2 Теоремы Роля, Лагранжа. 8
2.1.3 Теоремы Коши, Ферма. 9
2.1.4 Формула Тейлора. 10
2.1.5 Длина гладкой кривой. 11
2.1.6 Объем тела вращения. 13
2.1.7 Площадь поверхности тела вращения. 14
2.1.8 Понятие компакта. 16
2.1.9 Необходимые и достаточные условия локальных экстремумов. 17
2.1.10 Задачи на относительный экстремум. Правило множителей Лагранжа. 18
2.1.11 Теорема о замене переменных в кратных интегралах. Полярные, цилиндрические и сферические системы координат. Геометрический смысл Якобиана. 20
2.1.12 Потенциальные векторные поля. Критерии потенциального векторного поля. 23
2.1.13 Формула Грина. 24
2.1.14 Формула Гаусса–Остроградского. 25
2.1.15 Формула Стокса. 26
2.2 Математическое моделирование, математическое программирование, теория игр, численные методы. 29
2.2.1 Регрессионная модель. Однофакторная модель (построение модели, определение дисперсии, проверка адекватности) 29
2.2.2 Двойственная задача линейного программирования. 31
2.2.3 Производственная функция Кобба-Дугласа. Коэффициенты эластичности. 34
2.2.4 Модели расчета годовой производственной программы. Критерии в моделях. 35
2.2.5 Модель оптимальной загрузки оборудования для выпуска комплектной продукции. Виды комплектов. 37
2.2.6 Математическая обработка результатов опытов в планировании эксперимента. Полный факторный эксперимент. Свойства матрицы планирования. 38
2.2.7 Управление запасами материалов. Типы моделей. Простейшая модель Уилсона. 41
2.2.8 Сетевые графики. Критический путь. Оптимизация графика по времени в зависимости от вложенных средств. 42
2.2.9 Сетевые графики. Вероятностная сеть. Оценка времени выполнения работ. 45
2.2.10 Динамическое программирование. Распределение ресурсов между предприятиями головной фирмы. 47
2.2.11 Задачи раскроя материалов и составления смеси. Область применения. 50
2.2.12 Транспортная задача. Закрытая транспортная задача. 53
2.2.13 Открытая транспортная задача. 55
2.2.14 Матричные игры. Игры  и
и 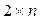 ............. 58
............. 58
2.2.15 Матричные игры 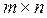 и линейное программирование. 62
и линейное программирование. 62
2.2.16 Методы решения нелинейных уравнений. 65
2.2.17 Методы решения систем линейных уравнений. 72
2.2.18 Нахождение наибольшего по модулю собственного числа матрицы. 77
2.2.19 Полиномиальное интерполирование. 78
2.2.20 Метод наименьших квадратов. 81
2.2.21 Численное интегрирование. 84
Список литературы. 86
ВВЕДЕНИЕ
Целью итоговой государственной аттестации является установление уровня подготовки студента к выполнению профессиональных задач и соответствия его подготовки требованиям государственного стандарта по данной специальности.
К итоговым аттестационным испытаниям допускаются лица, успешно завершившие в полном объеме освоение основной образовательной программы по специальности.
По специальности «Прикладная математика» для квалификации «дипломированный специалист» итоговая аттестация содержит формы: дипломная работа и государственный экзамен.
Итоговый экзамен проводится в форме итогового междисциплинарного экзамена по дисциплинам: математический анализ, математическое моделирование, методы оптимизации (математическое программирование), теория игр, численные методы.
Настоящее пособие содержит программу государственных экзаменов и методические указания по подготовке к экзаменам.
Перед работой с методическими указаниями необходимо проработать соответствующий лекционный материал и просмотреть набор задач, относящийся к данной теме.
Математический анализ
1. Теоремы Вейерштрасса.
2. Теоремы Роля, Лагранжа.
3. Теоремы Коши, Ферма.
4. Формула Тейлора.
5. Длина гладкой кривой.
6. Объем тела вращения.
7. Площадь поверхности тела вращения.
8. Понятие компакта.
9. Необходимые и достаточные условия локальных экстремумов.
10. Задачи на относительный экстремум. правило множителей Лагранжа.
11. Теорема о замене переменных в кратных интегралах. Полярные, цилиндрические и сферические системы координат. Геометрический смысл Якобиана.
12. Потенциальные векторные поля. Критерии потенциального векторного поля.
13. Формула Грина.
14. Формула Гаусса–Остроградского.
15. Формула Стокса.
Математический анализ
Теоремы Вейерштрасса
Теоремы Роля, Лагранжа
Теорема Ролля. Пусть функция 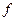 непрерывна на отрезке
непрерывна на отрезке 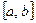 , имеет производную на интервале
, имеет производную на интервале 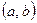 и принимает равные значения на его концах
и принимает равные значения на его концах  . Тогда на интервале
. Тогда на интервале 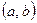 существует, по крайней мере, одна точка
существует, по крайней мере, одна точка 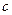 , в которой производная зануляется
, в которой производная зануляется 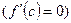 .
.
Теорема Лагранжа. Пусть функция 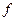 непрерывна на отрезке
непрерывна на отрезке 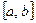 , имеет производную на интервале
, имеет производную на интервале 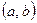 . Тогда на интервале
. Тогда на интервале 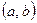 существует точка
существует точка 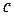 , для которой выполняется равенство
, для которой выполняется равенство  .
.
Теорема Лагранжа имеет простой геометрический смысл. Действительно, 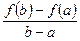 есть тангенс угла наклона секущей, проходящей через точки
есть тангенс угла наклона секущей, проходящей через точки 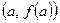 и
и 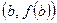 , а
, а 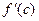 – тангенс угла наклона касательной в точке
– тангенс угла наклона касательной в точке  , следовательно, рассматриваемые секущая и касательная параллельны.
, следовательно, рассматриваемые секущая и касательная параллельны.
Пример 2.1.2.1. Показать, что функция 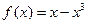
 на отрезках
на отрезках 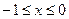 и
и 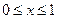 удовлетворяет условиям теоремы Ролля. Найти соответствующие значения
удовлетворяет условиям теоремы Ролля. Найти соответствующие значения 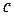 .
.
Решение.
Функция 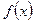 непрерывна и дифференцируема для всех значений
непрерывна и дифференцируема для всех значений 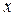 ; кроме того,
; кроме того, 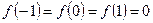 . Следовательно, теорема Ролля применима на отрезках
. Следовательно, теорема Ролля применима на отрезках 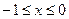 и
и 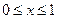 . Для нахождения числа
. Для нахождения числа 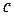 составляем уравнение:
составляем уравнение: 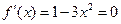 . Отсюда
. Отсюда 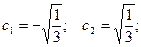
 причем
причем 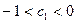 ;
; 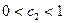 .
.
Пример 2.1.2.2. Проверить выполнение теоремы Лагранжа для функции 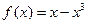 на отрезке
на отрезке  и найти соответствующее промежуточное значение
и найти соответствующее промежуточное значение 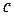 .
.
Решение.
Функция 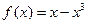 непрерывна и дифференцируема для всех значений
непрерывна и дифференцируема для всех значений  , причем
, причем  . Отсюда по формуле Лагранжа имеем,
. Отсюда по формуле Лагранжа имеем, 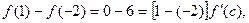 т. е.
т. е. 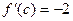 .
.
Следовательно, 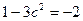 и
и 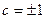 ; подходит только значение
; подходит только значение 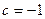 , для которого справедливо неравенство
, для которого справедливо неравенство  .
.
Теоремы Коши, Ферма
Теорема Коши. Пусть функции 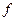 и
и 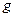 непрерывны на отрезке
непрерывны на отрезке 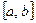 , имеют производные
, имеют производные  и
и 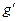 на интервале
на интервале 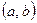 одновременно не обращающиеся в
одновременно не обращающиеся в 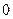 ,
, 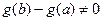 . Тогда на интервале
. Тогда на интервале 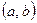 существует точка
существует точка 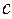 , для которой выполняется равенство
, для которой выполняется равенство 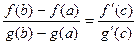 .
.
Теорема Ферма. Пусть функция 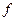 достигает в точке
достигает в точке 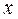 локального экстремума (максимума или минимума) и в ней существует производная, тогда
локального экстремума (максимума или минимума) и в ней существует производная, тогда 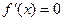 .
.
Пример 2.1.3.1. Для функции 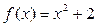 и
и 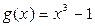 проверить выполнение условий теоремы Коши на отрезке
проверить выполнение условий теоремы Коши на отрезке 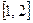 и найти
и найти 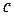 .
.
Решение.
Проверим выполнение условий теоремы Коши. Функции 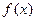 и
и 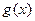 непрерывны на отрезке
непрерывны на отрезке 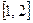 и при
и при  имеют производные, не обращающиеся в нуль одновременно, причем
имеют производные, не обращающиеся в нуль одновременно, причем 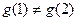 .
.
Тогда по теореме Коши
 или
или 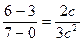 . Отсюда
. Отсюда 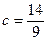 , где
, где 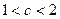 .
.
Пример 2.1.3.2. Для функции 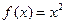 проверить выполнение условий теоремы Ферма.
проверить выполнение условий теоремы Ферма.
Решение.
Очевидно, функция 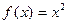 имеет минимум в точке
имеет минимум в точке 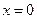 . Так как
. Так как 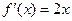 , то
, то  , как и утверждает теорема Ферма.
, как и утверждает теорема Ферма.
Формула Тейлора
Основным свойством дифференциального исчисления является формула Тейлора, позволяющая приближать функции специальными многочленами в окрестности некоторой точки. Мы рассмотрим формулу Тейлора с остаточным членом в форме Лагранжа (глобальная формула Тейлора) и с остаточным членом в форме Пеано (локальная формула Тейлора).
Пусть функция 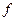 в некотором интервале
в некотором интервале 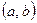 имеет
имеет 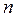 производных, тогда для любой точки
производных, тогда для любой точки 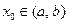 можно написать многочлен Тейлора
можно написать многочлен Тейлора
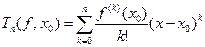 .
.
Разность 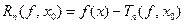 называется остаточным членом формулы Тейлора, это выражение может быть преобразовано различными способами, которые приводят к разным формам остаточного члена.
называется остаточным членом формулы Тейлора, это выражение может быть преобразовано различными способами, которые приводят к разным формам остаточного члена.
Теорема (остаточный член в форме Пеано). Пусть функция 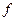 в некотором интервале
в некотором интервале 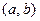 имеет
имеет 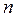 непрерывных производных, тогда для любой точки
непрерывных производных, тогда для любой точки 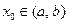 при
при 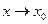 имеет место равенство:
имеет место равенство:
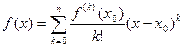 .
.
Теорема (остаточный член в форме Лагранжа). Пусть функция 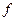 в некотором интервале
в некотором интервале 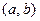 , содержащем точку
, содержащем точку 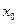 , имеет
, имеет 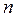 производных, а во всех точках этого интервала, кроме, быть может, точки
производных, а во всех точках этого интервала, кроме, быть может, точки 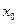 , имеет
, имеет 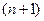 -ю производную; тогда для любого
-ю производную; тогда для любого 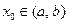 ,
, 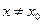 существует
существует  , находящееся между
, находящееся между 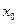 и
и  , для которой выполнено равенство:
, для которой выполнено равенство:
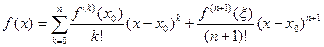 .
.
Заметим, что при 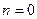 последняя теорема превращается в теорему Лагранжа.
последняя теорема превращается в теорему Лагранжа.
Формулу Тейлора в точке  обычно называют формулой Маклорена. В этом случае удобно положить
обычно называют формулой Маклорена. В этом случае удобно положить 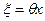 , т.е.
, т.е. 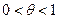 .
.
Пример 2.1.4.1. Разложить по формуле Маклорена функцию 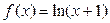 .
.
Решение.
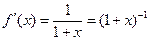 ,
,
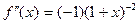 ,
,
…
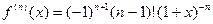 .
.
Тогда 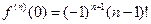 ,
,  и так как
и так как 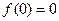 , то
, то  ,
,  .
.
Пример 2.1.4.2. Функцию 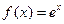 разложить по степеням бинома
разложить по степеням бинома 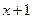 до члена, содержащего
до члена, содержащего 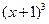 .
.
Решение.
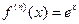 для всех
для всех 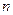 ,
, 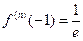 . Следовательно,
. Следовательно,
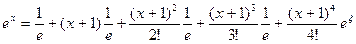 , где
, где  ,
, 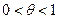 .
.
Длина гладкой кривой
Рассмотрим некоторую функцию  . Для фиксированного значения
. Для фиксированного значения  – есть некоторая точка
– есть некоторая точка 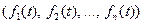 в
в 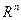 . Такую функцию называют параметрическим представлением кривой
. Такую функцию называют параметрическим представлением кривой 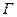 в пространстве
в пространстве 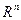 (роль параметра играет переменная
(роль параметра играет переменная 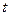 ). Кривая
). Кривая 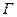 называется непрерывной (соответственно гладкой), если все функции
называется непрерывной (соответственно гладкой), если все функции 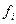 являются непрерывными (соответственно непрерывно дифференцируемыми). Пусть
являются непрерывными (соответственно непрерывно дифференцируемыми). Пусть  – некоторое разбиение отрезка
– некоторое разбиение отрезка  ; рассмотрим точки
; рассмотрим точки 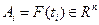 и ломаную
и ломаную 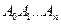 , которая получается последовательным соединением точек
, которая получается последовательным соединением точек  и
и  прямолинейными отрезками. Такие ломаные называют вписанными в кривую
прямолинейными отрезками. Такие ломаные называют вписанными в кривую 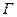 . Пусть
. Пусть 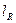 – длина ломаной
– длина ломаной 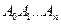 .
.

Кривая называется спрямляемой, если конечна величина 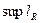 , где верхняя грань берется по всем вписанным в
, где верхняя грань берется по всем вписанным в 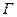 ломаным. За значение длины кривой
ломаным. За значение длины кривой 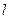 как раз и принимают указанную величину.
как раз и принимают указанную величину.
Оказывается, что для гладких кривых существует достаточно простой способ вычисления длинны 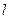 .
.
Теорема: Гладкая кривая является спрямляемой, причем для ее длины 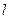 справедлива следующая формула:
справедлива следующая формула:
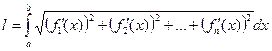 .
.
 Пример 2.1.5.1. Найти длину астроиды
Пример 2.1.5.1. Найти длину астроиды 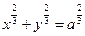 .
.
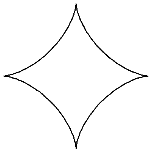 Решение.
Решение.
Дифференцируя уравнение астроиды, получим 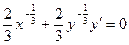 , отсюда
, отсюда  .
.
Поэтому для длины дуги одной четверти астроиды имеем:
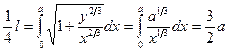 .
.
Отсюда 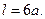
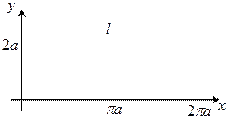 Пример 2.1.5.2. Найти длину одной арки циклоиды
Пример 2.1.5.2. Найти длину одной арки циклоиды 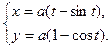

Решение.
Имеем 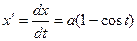 и
и 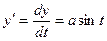 . Поэтому
. Поэтому
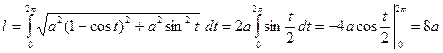 .
.
Пределы интегрирования 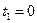 и
и 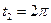 соответствуют крайними точкам арки циклоиды.
соответствуют крайними точкам арки циклоиды.

 Пример 2.1.5.3. Найти всю длину кардиоиды
Пример 2.1.5.3. Найти всю длину кардиоиды 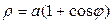 .
.
Решение.
В силу симметрии кривой найдем сначала половину длины. Поскольку 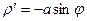 , получим:
, получим:

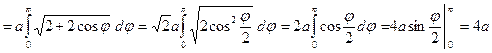 .
.
Отсюда 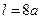 .
.
Объем тела вращения
Пусть 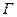 – кривая, описываемая в декартовой системе координат на плоскости непрерывной неотрицательной функцией
– кривая, описываемая в декартовой системе координат на плоскости непрерывной неотрицательной функцией 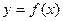
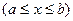 . Рассмотрим формулу для вычисления
. Рассмотрим формулу для вычисления 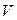 – объема тела вращения, ограниченного плоскостями
– объема тела вращения, ограниченного плоскостями 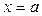 и
и 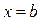 и поверхностью вращения кривой
и поверхностью вращения кривой 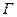 вокруг оси
вокруг оси 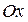 в трехмерном пространстве.
в трехмерном пространстве.
Теорема. Для величины 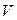 справедлива следующая формула:
справедлива следующая формула:
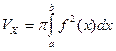 .
.
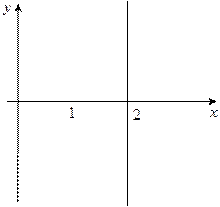
 Пример 2.1.6.1. Найти объем тела, образованного вращением вокруг оси
Пример 2.1.6.1. Найти объем тела, образованного вращением вокруг оси 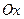 фигуры, ограниченной кривой
фигуры, ограниченной кривой 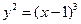 и прямой
и прямой  .
.
Решение.
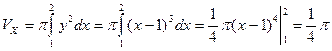 .
.
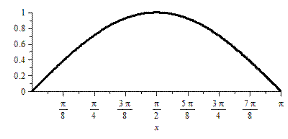
Пример 2.1.6.2. Вычислить объем тела, образованного вращением фигуры, ограниченной одной полуволной синусоиды 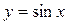 и отрезком
и отрезком 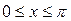 оси
оси 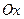 вокруг оси
вокруг оси 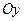 .
.
Решение.
Воспользуемся формулой 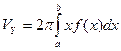 . Тогда
. Тогда
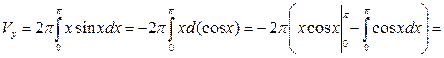
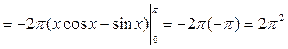 .
.
Пример 2.1.6.3. Вычислить объем тела, полученного вращением вокруг оси 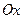 одной арки циклоиды
одной арки циклоиды 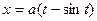 ,
, 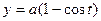
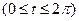 .
.
Решение:
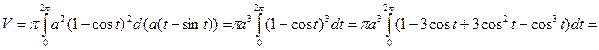
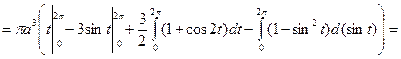
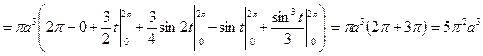 .
.
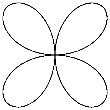 Пример 2.1.6.4. Определить объем, образованный вращением кривой
Пример 2.1.6.4. Определить объем, образованный вращением кривой 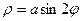 вокруг полярной оси.
вокруг полярной оси.
Решение.
Воспользуемся формулой 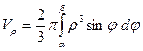 .
.
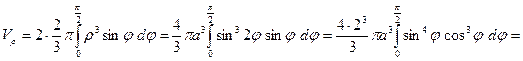
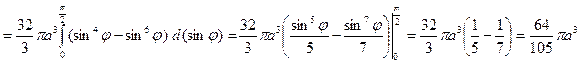 .
.
Понятие компакта
Компакты
 Определение. Множество
Определение. Множество 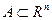 называется компактным множеством (компактом), если из любой последовательности точек этого множества можно извлечь подпоследовательность, сходящуюся к некоторой точке множества
называется компактным множеством (компактом), если из любой последовательности точек этого множества можно извлечь подпоследовательность, сходящуюся к некоторой точке множества 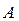 .
.
Теорема (критерий компактности). Множество 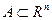 является компактом тогда и только тогда, когда оно замкнуто и ограничено.
является компактом тогда и только тогда, когда оно замкнуто и ограничено.
Определение. Пусть нам дан набор множеств  ,
, 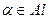 (
( 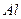 называется индексным множеством). Совокупность индексированных множеств
называется индексным множеством). Совокупность индексированных множеств  называется семейством.
называется семейством.
Определение. Пусть дано множество 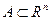 и семейство множеств
и семейство множеств 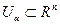 . Семейство множеств
. Семейство множеств 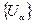 называется покрытием множества
называется покрытием множества 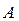 , если
, если 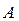 содержится в объединении всех множеств рассматриваемого семейства
содержится в объединении всех множеств рассматриваемого семейства  .
.
Определение. Говорят, что 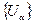 – открытое покрытие множества
– открытое покрытие множества 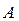 , если:
, если:
1. 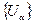 – покрытие
– покрытие 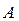 ,
,
2. каждое 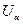 – открытое множество.
– открытое множество.
Определение. Покрытие  называется подпокрытием покрытия
называется подпокрытием покрытия 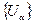 , если любой элемент покрытия
, если любой элемент покрытия 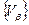 является элементом покрытия
является элементом покрытия 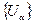 , то есть для всех
, то есть для всех 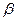 существует такое
существует такое 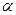 , что
, что 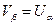 .
.
Теорема Бореля. Множество 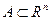 – компакт тогда и только тогда, когда из любого открытого покрытия множества
– компакт тогда и только тогда, когда из любого открытого покрытия множества  можно извлечь конечное подпокрытие.
можно извлечь конечное подпокрытие.
Пример 2.1.8.1. Показать, что отрезок  является компактным множеством в этом пространстве.
является компактным множеством в этом пространстве.
Решение.
Поскольку отрезок 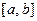 является ограниченным множеством, следовательно, из любой последовательности его элементов можно извлечь подпоследовательность, которая имеет конечный предел (теорема Больцано-Вейерштрасса). В силу теоремы о предельном переходе в неравенстве (см. [17] гл. 2 теорема 1.3), предел такой последовательности принадлежит отрезку
является ограниченным множеством, следовательно, из любой последовательности его элементов можно извлечь подпоследовательность, которая имеет конечный предел (теорема Больцано-Вейерштрасса). В силу теоремы о предельном переходе в неравенстве (см. [17] гл. 2 теорема 1.3), предел такой последовательности принадлежит отрезку 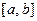 . Таким образом, по определению промежуток
. Таким образом, по определению промежуток 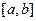 является компактным множеством.
является компактным множеством.
Полярные координаты
Введем на плоскости полярную систему координат, согласованную с заданной декартовой (  – полярная ось,
– полярная ось,  – расстояние от точки до полюса
– расстояние от точки до полюса 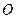 ,
, 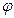 – угол между радиусом-вектором точки и полярной осью).
– угол между радиусом-вектором точки и полярной осью).
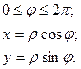
 |
Данная система уравнений осуществляет преобразование полярных координат в декартовы. Правые части – непрерывно дифференцируемые функции с якобианом
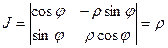 .
.
Если  ;
; 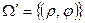 , то
, то 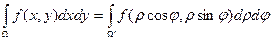 .
.
Сферические координаты
Пусть заданы полярные координаты в плоскости 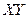 ,
, 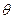 – угол между радиусом-вектором точки и плоскостью
– угол между радиусом-вектором точки и плоскостью 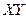 .
.
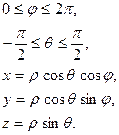
 |
Если 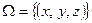 ,
, 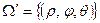 то
то
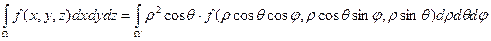 . (ОШИБКА)
. (ОШИБКА)
Цилиндрические координаты
 В плоскости
В плоскости 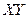 вводим полярные координаты
вводим полярные координаты 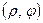 . Тогда координаты
. Тогда координаты 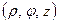 называются цилиндрическими.
называются цилиндрическими.
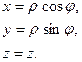
Эти равенства связывают цилиндрические координаты с декартовыми координатами. Здесь 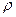 – расстояние от проекции точки
– расстояние от проекции точки 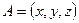 на плоскость
на плоскость 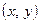 до начала координат декартовой системы, а
до начала координат декартовой системы, а 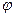 – угол между радиусом-вектором указанной проекции и осью
– угол между радиусом-вектором указанной проекции и осью 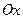 . Якобиан преобразования легко вычисляется.
. Якобиан преобразования легко вычисляется.
 .
.
Если 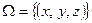 ;
; 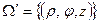 то
то
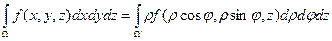 .
.
Пример 2.1.11.1. Перейдя к полярным координатам, вычислить двойной интеграл 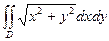 , если
, если 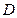 – I четверть круга
– I четверть круга 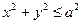 .
.
Решение.
Полагая 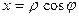 ,
, 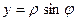 имеем
имеем
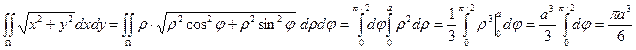 .
.
 Пример 2.1.11.2. Вычислить объем тела, ограниченного поверхностями:
Пример 2.1.11.2. Вычислить объем тела, ограниченного поверхностями: 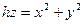 ,
, 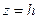 .
.
Решение.
Данное тело ограничено снизу параболоидом  , сверху плоскостью
, сверху плоскостью 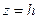 и проецируется в круг
и проецируется в круг  плоскости
плоскости 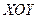 . Используем цилиндрические координаты, в которых уравнение параболоида примет вид
. Используем цилиндрические координаты, в которых уравнение параболоида примет вид 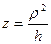 . Объем тела равен
. Объем тела равен
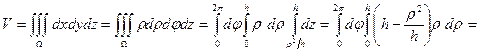
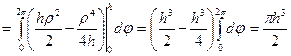 .
.
Пример 2.1.11.3. Вычислить 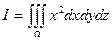 , если
, если 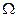 – шар
– шар 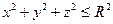 .
.
Решение.
Перейдем к сферическим координатам. В области 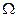 координаты
координаты 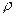 ,
, 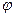 и
и 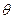 изменяются так:
изменяются так: 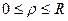 ,
, 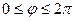 ,
,  . Следовательно,
. Следовательно,
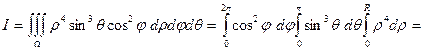
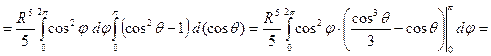
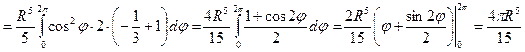 .
.
2.1.12 Потенциальные векторные поля.
Критерии потенциального векторного поля
Формула Грина
Теорема (формула Грина). Пусть в области 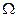 задано гладкое векторное поле
задано гладкое векторное поле 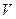 , также задано множество
, также задано множество 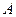 в
в 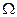 с кусочно-гладкой границей, которая правильно ориентирована, тогда справедлива следующая формула:
с кусочно-гладкой границей, которая правильно ориентирована, тогда справедлива следующая формула:
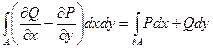 ,
,
где  ,
,  – координаты векторного поля.
– координаты векторного поля.
Пример 2.1.13.1. Применяя формулу Грина, вычислить
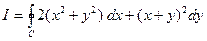 , если
, если  – контур треугольника с вершинами
– контур треугольника с вершинами 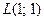 ,
, 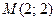 ,
, 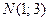 , пробегаемый против хода часовой стрелки. Проверить результат непосредственным интегрированием.
, пробегаемый против хода часовой стрелки. Проверить результат непосредственным интегрированием.
Решение.
 ,
, 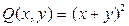 . Находим
. Находим  . Таким образом,
. Таким образом,
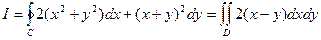 , где область
, где область  – треугольник
– треугольник 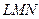 . Уравнение прямой
. Уравнение прямой  , уравнение
, уравнение 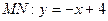 . Вычислим двойной интеграл по данной области:
. Вычислим двойной интеграл по данной области:
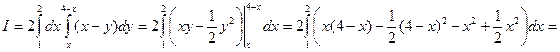
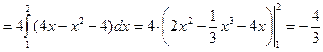 .
.
Вычислим теперь непосредственно криволинейный интеграл по контуру  , состоящему из звеньев
, состоящему из звеньев 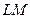 ,
, 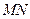 ,
,  :
:
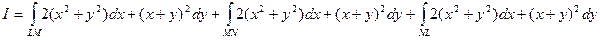 .
.
Уравнение 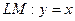 ; следовательно
; следовательно 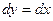 ,
,  .
.
Уравнение 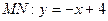 ; следовательно
; следовательно 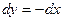 ,
,  .
.
Уравнение 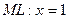 ; значит
; значит 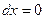 ,
,  .
.
Таким образом,
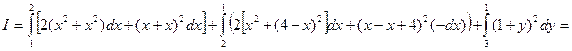
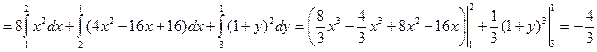 .
.
Пример 2.1.13.2. Применяя формулу Грина, вычислить 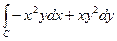 , где
, где  – окружность
– окружность 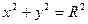 , пробегая против хода часовой стрелки.
, пробегая против хода часовой стрелки.
Решение.
Здесь  ,
,  . Тогда
. Тогда 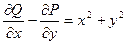 . Следовательно,
. Следовательно,
 .
.
Поверхностные интегралы
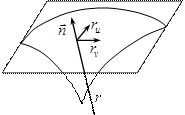 Рассмотрим открытое множество
Рассмотрим открытое множество  , точки которого будем обозначать
, точки которого будем обозначать 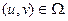 . Пусть
. Пусть 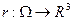 – дифференцируемая функция,
– дифференцируемая функция,  .
.
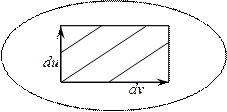 Образ отображения
Образ отображения  представляет собой при некоторых дополнительных предположениях двухмерную поверхность в
представляет собой при некоторых дополнительных предположениях двухмерную поверхность в 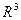 .
.
Рассмотрим векторы
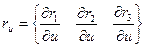 ;
;
 .
.
Они будут касательными к поверхности в текущей точке.
Потребуем, чтобы матрица, состоящая из векторов  и
и  , имела ранг 2. Тогда
, имела ранг 2. Тогда 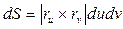 – элемент площади поверхности,
– элемент площади поверхности, 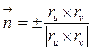 – единичные нормали в текущей точке поверхности.
– единичные нормали в текущей точке поверхности.
Определение. Поверхность ориентируема, если в каждой точке поверхности можно определить нормаль так, чтобы нормали непрерывно изменялись от точки к точке. Такую поверхность также называют двухсторонней.
Формула Стокса
Определение. Ротор (вихрь) векторного поля 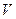 задается следующей формулой:
задается следующей формулой:
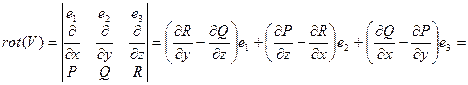
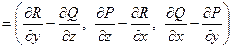 .
.
Формула Стокса
 Пусть дана ориентированная полем единичных нормалей гладкая поверхность
Пусть дана ориентированная полем единичных нормалей гладкая поверхность  в
в  , граница
, граница  состоит из конечного числа гладких кривых.
состоит из конечного числа гладких кривых.
Рассмотрим кривую 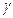 (один из кусков границы). Зададим ориентацию
(один из кусков границы). Зададим ориентацию 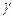 так, чтобы направление обхода было согласовано с вектором нормали. Будем обходить кривую
так, чтобы направление обхода было согласовано с вектором нормали. Будем обходить кривую 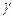 так, что если смотреть на поверхность с конца нормали, то обход границы осуществляется в том же направлении, в каком поворот вектора
так, что если смотреть на поверхность с конца нормали, то обход границы осуществляется в том же направлении, в каком поворот вектора  ортонормированного правильного базиса
ортонормированного правильного базиса 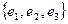
 до совмещения с вектором
до совмещения с вектором 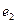 меньше. Тогда ориентированная граница называется согласованно ориентированной с ориентацией поверхности. Зададим гладкое векторное поле
меньше. Тогда ориентированная граница называется согласованно ориентированной с ориентацией поверхности. Зададим гладкое векторное поле 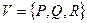 в окрестности поверхности.
в окрестности поверхности.
Теорема (формула Стокса). В условиях, приведенных выше, справедлива формула:
 .
.
Пример 2.1.15.1. Применяя формулу Стокса, найти 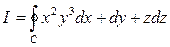 , если
, если 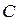 – окружность
– окружность  ,
, 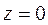 .
.
Решение.
Радиус-вектор для окружности  ,
, 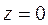 равен
равен 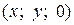 . Тогда
. Тогда
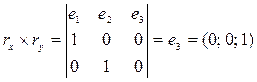 ;
;
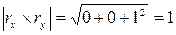 ;
;
 ;
;
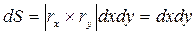 .
.
Учитывая, что 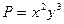 ,
, 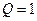 ,
, 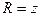 , получим
, получим
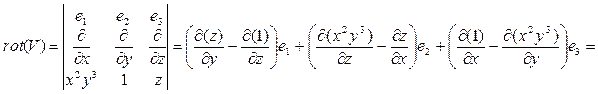
 .
.
По формуле Стокса получаем
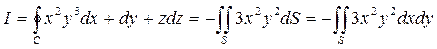 ,
,
где плоская область 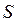 ограничена окружностью
ограничена окружностью 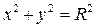 . Вводя полярные координаты
. Вводя полярные координаты 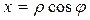 ,
, 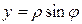 , получим
, получим
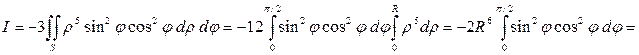
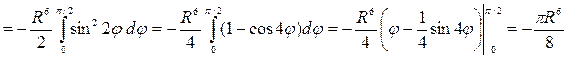 .
.
Метод половинного деления
Пусть дано нелинейное уравнение 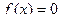 и отделен простой корень
и отделен простой корень 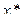 на отрезке
на отрезке 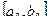 , выполняется условие
, выполняется условие  и
и 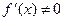 ,
,  и
и  сохраняет знак. Требуется уточнить местоположение корня уравнения с заданной точностью
сохраняет знак. Требуется уточнить местоположение корня уравнения с заданной точностью  .
.
Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности 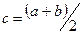 , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция
, и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция 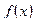 принимает различные знаки.
принимает различные знаки.
Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины  , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
, задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
Метод имеет линейную, но безусловную сходимость, его погрешность за каждую итерацию уменьшается в 2 раза:
 .
.
Методика решения нелинейного уравнения
методом половинного деления
1. Найти начальный интервал неопределенности 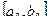 одним из методов отделения корней, задать малое положительное число
одним из методов отделения корней, задать малое положительное число  и присвоить
и присвоить 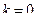 .
.
2. Найти середину текущего интервала 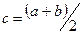 .
.
3. Если 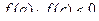 , то
, то 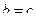 , иначе
, иначе 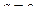 .
.
4. Если 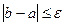 , то процесс завершить:
, то процесс завершить:  , иначе
, иначе  и перейти к п.2.
и перейти к п.2.
Пример 2.2.16.4. Найти корень уравнения методом половинного деления  с точностью
с точностью 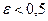 на интервале
на интервале 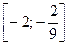 .
.
Решение.
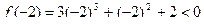 ,
,
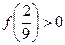 ,
,
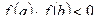 ,
,
1)  ,
, 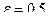 .
.
2)  .
.
Если 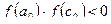 , тогда
, тогда 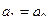 ,
, 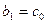 , иначе
, иначе 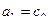 ,
,  .
.
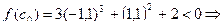
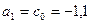 ,
, 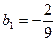 .
.
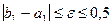
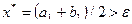 , иначе
, иначе 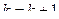 .
.
2) 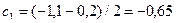 ,
,
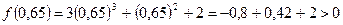 ,
,
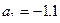 ,
,
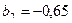 ,
,
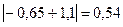 ,
,
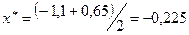 .
.
Метод итераций
Если данное уравнение 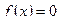 приведено к виду
приведено к виду 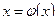 , где
, где 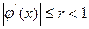 всюду на отрезке
всюду на отрезке 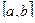 , на котором исходное уравнение имеет единственный корень, то исходя из некоторого начального значения
, на котором исходное уравнение имеет единственный корень, то исходя из некоторого начального значения  , принадлежащего отрезку
, принадлежащего отрезку 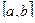 , можно построить такую последовательность:
, можно построить такую последовательность:
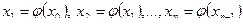 .
.
Пределом этой последовательности является единственный корень уравнения 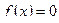 на отрезке
на отрезке 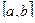 .
.
Метод Гаусса
Метод Гаусса состоит в исключении слагаемых системы путем ее равносильного преобразования. Метод разбивается на две совокупности операций, которые разбиваются условно на прямой и обратный ход.
а) Прямой ход состоит в исключении элементов, расположенных ниже элементов, соответствующих главной диагонали матрицы  . Матрица
. Матрица  преобразуется к верхнетреугольному виду с единицами на главной диагонали.
преобразуется к верхнетреугольному виду с единицами на главной диагонали.
б) Обратный ход, из матрицы 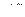 определяем последовательно
определяем последовательно 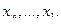
Надо решить систему алгебраических уравнений  :
:
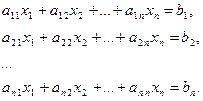
Нужно преобразовать к треугольной матрице.
Прямой ход, в общем случае коэффициенты матрицы рассчитываются в виде:
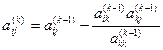 ,
,  , (2.17.3)
, (2.17.3)
где 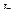 – номер шага
– номер шага 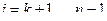 ,
, 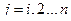 .
.
Получим
 .
.
Обратный ход, начиная с последнего уравнения, последовательно определяем 
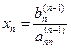 ,
,
 . (2.17.4)
. (2.17.4)
Изложенный метод имеет ограничение, связанное с тем, что ведущие элементы 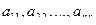 и т.д. должны быть отличны от нуля и не должны быть малыми по модулю, поскольку погрешности вычислений будут большими.
и т.д. должны быть отличны от нуля и не должны быть малыми по модулю, поскольку погрешности вычислений будут большими.
Порядок последовательности исключения неизвестных может сильно сказаться на результатах расчетов. Наиболее надежным является метод Гаусса с выбором главного элемента.
Метод простой итерации
Для решения систему линейных уравнений  приводим к каноническому виду:
приводим к каноническому виду:
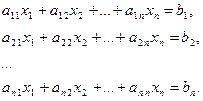 (2.17.6)
(2.17.6)
Выразим  :
:

Таким образом, получим 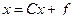 , где
, где

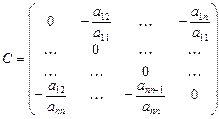 ,
, 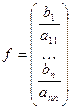 ,
,  . (2.17.7)
. (2.17.7)
Итерационный процесс запишется виде:
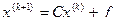 . (2.17.8)
. (2.17.8)
Начальное приближение 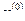 выбирается произвольно, но требуется выполнение условия сходимости, норма матрицы
выбирается произвольно, но требуется выполнение условия сходимости, норма матрицы 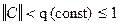 . Сходящийся процесс обладает свойством самоисправляемости. Условие сходимости выполняется, если в матрице
. Сходящийся процесс обладает свойством самоисправляемости. Условие сходимости выполняется, если в матрице  диагональные элементы преобладают. Иначе модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов. Чем меньше величина нормы матрицы
диагональные элементы преобладают. Иначе модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов. Чем меньше величина нормы матрицы 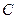 , тем быстрее сходится метод.
, тем быстрее сходится метод.
Для того чтобы данный процесс сходился, необходимо, чтобы норма матрицы 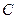 была меньше 1 или выполнялись следующие условия:
была меньше 1 или выполнялись следующие условия:
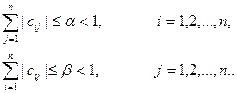 (2.17.9)
(2.17.9)
Тогда справедливы оценки скорости сходимости:
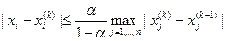 ,
,
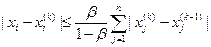 . (2.17.10)
. (2.17.10)
Методика решения систем линейных уравнений
методом простой итерации
1. Преобразовать систему  к виду
к виду 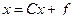 .
.
2. Проверить условие сходимости 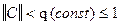 . Задать начальное приближение
. Задать начальное приближение  и точность
и точность 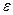 . Положить
. Положить 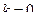 .
.
3. Вычислить приближение по формуле 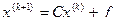 .
.
4. Если выполнено условие  , то процесс завершить и положить
, то процесс завершить и положить 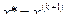 , иначе
, иначе 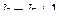 перейти к пункту 3.
перейти к пункту 3.
Пример 2.2.17.2. Для системы линейных алгебраических уравнений построить сходящийся итерационный процесс:
Решение.
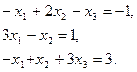
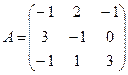 .
.
Матрица этой системы не имеет диагонального преобладания.
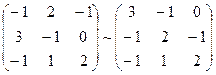 .
.
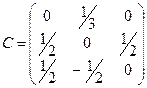 ,
,  ,
,  .
.
Достаточное условие сходимости метода простых итераций 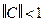 выполняется. Поэтому сначала проведем преобразование.
выполняется. Поэтому сначала проведем преобразование.
 .
.
Возьмем
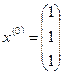 , тогда
, тогда
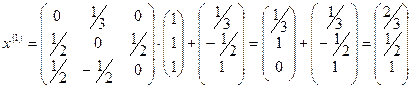 ,
,
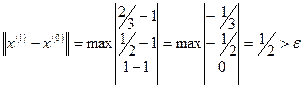 ,
,
 ,
,
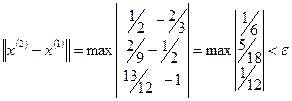 .
.
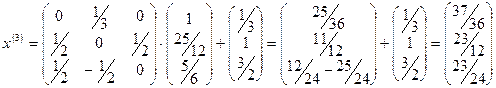 ,
,
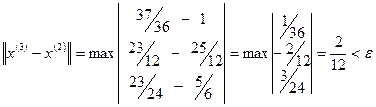 .
.
Видно, что норма разности между двумя последовательными приближениями с увеличением номера итерации уменьшается, что характеризует сходящийся процесс (этот вывод относится ко всем приведенным примерам). Видно также, что, начиная со 2-й итерации,  с увеличением
с увеличением  увеличиваются и уменьшаются соответственно, и они стремятся к верному (точному) решению:
увеличиваются и уменьшаются соответственно, и они стремятся к верному (точному) решению: 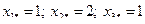 .
.
2.2.18 Нахождение наибольшего по модулю
собственного числа матрицы
Корни характеристического уравнения  являются
являются 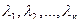 собственными значениями матрицы
собственными значениями матрицы  .
.
Пусть 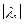 наибольший по модулю. Матрица с действительными и положительными коэффициентами имеем наибольшее действительное собственное значение.
наибольший по модулю. Матрица с действительными и положительными коэффициентами имеем наибольшее действительное собственное значение.
В качестве начального собственного вектора возьмем произвольный вектор 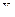 . Тогда
. Тогда 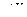 назовем итерацией вектора
назовем итерацией вектора 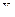 , которая образуется путем перемножения
, которая образуется путем перемножения 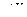 ,
, 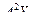 , …,
, …, 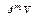 ;
;
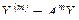 .
.
Приближенное наибольшего по модулю собственного значения:
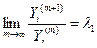 ,
, 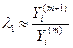 , при
, при 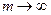 .
.
Для ускорения сходимости можно составить последовательность  и т.д.
и т.д.
Методика решения задачи нахождения наибольшего
собственного значения матрицы
1. Выбрать произвольное начальное приближение собственного вектора 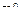 ,
, 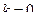 .
.
2. Найти 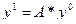 ,
, 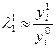 , где
, где 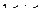 и
и 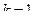 .
.
3. Вычислить 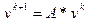 .
.
4. Найти 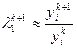 , где
, где 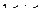 .
.
5. Если 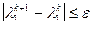 , то процесс завершить и положить
, то процесс завершить и положить 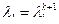 , иначе
, иначе 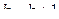 и перейти к п.3.
и перейти к п.3.
Пример 2.2.18.1. Найти наибольшее собственное значение матрицы 
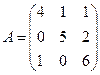 , с точностью
, с точностью  .
.
Решение.
Пусть  , тогда значение наибольшего собственного значения на нулевой итерации равно
, тогда значение наибольшего собственного значения на нулевой итерации равно 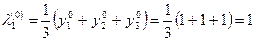 ,
,
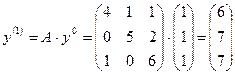 .
.
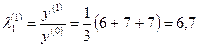 ,
,
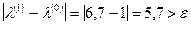 .
.
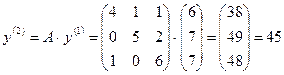 ,
,
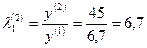 ,
,
 .
.
Метод наименьших квадратов
Задана таблица значений аргументов 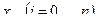 и соответствующих значений функции
и соответствующих значений функции  .
.
На практике удобно представить искомую зависимость в виде многочлена, линейной комбинации некоторых базисных функций:
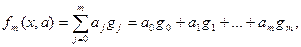 (2.20.1)
(2.20.1)
где 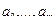 – неизвестные коэффициенты,
– неизвестные коэффициенты, 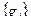 – заданная система базисных функций. В качестве базисных функций могут выбираться, например, степенные функции, полиномы Чебышева, тригонометрические функции
– заданная система базисных функций. В качестве базисных функций могут выбираться, например, степенные функции, полиномы Чебышева, тригонометрические функции  .
.
Условия согласования метода сглаживания – метод наименьших квадратов:
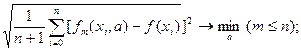 . (2.20.2)
. (2.20.2)
Отметим отличительные особенности решения задачи сглаживания методом наименьших квадратов:
1. Метод наименьших квадратов требует выполнения условия соответствия  и
и 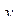 в среднем.
в среднем.
2. Количество точек 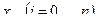 , в которых задана исходная функция, значительно больше, чем степень многочлена.
, в которых задана исходная функция, значительно больше, чем степень многочлена.
Численное интегрирование
Формула трапеции
Разобьем отрезок 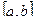 на
на 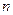 равных частей точками
равных частей точками  , каждая длиной
, каждая длиной 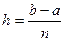 и найдем
и найдем 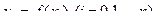 , тогда формула трапеции:
, тогда формула трапеции:
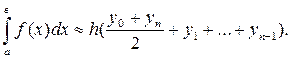
Оценка погрешности:
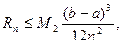 где
где 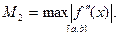
Формула Симпсона
Разобьем отрезок 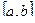 на
на 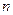 равных частей точками
равных частей точками  , каждая длиной
, каждая длиной 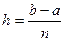 и найдем
и найдем 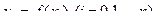 , но теперь возьмем четное число
, но теперь возьмем четное число 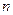 , тогда формула Симпсона:
, тогда формула Симпсона:
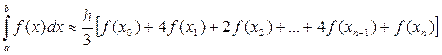 .
.
Оценка погрешности:
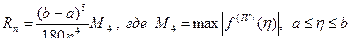 .
.
Другой способ оценки погрешности. Если отыскание четвертой производной подынтегральной функции затруднительно, то оценку погрешности вычисления интеграла  по формуле Симпсона можно получить по методу удвоения шага вычислений.
по формуле Симпсона можно получить по методу удвоения шага вычислений.
Полагая  , вычисляют приближенное значение данного интеграла по формуле Симпсона для шага
, вычисляют приближенное значение данного интеграла по формуле Симпсона для шага  . Погрешность определяется формулой:
. Погрешность определяется формулой:
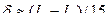 ,
,
где  – найденное значение интеграла при шаге
– найденное значение интеграла при шаге  ,
,
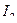 – найденное значение интеграла при шаге
– найденное значение интеграла при шаге 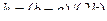 .
.
Пример 2.2.21.1. Вычислить определенный интеграл методом трапеции с шагом 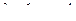 . Найти оценку погрешности.
. Найти оценку погрешности.
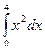 .
.
Решение.
Формула трапеции:
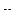
| 0 | 1 | 2 | 3 | 4 |

| 0 | 1 | 4 | 9 | 16 |
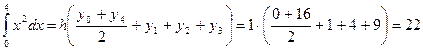 .
.
Оценка погрешности:

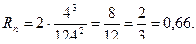
Точное решение:
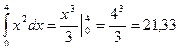 , погрешность ~0,66.
, погрешность ~0,66.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 5
1 ПРОГРАММА ГОСУДАРСТВЕННЫХ ЭКЗАМЕНОВ. 6
2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВОПРОСАМ ПРОГРАММЫ.. 8
2.1 Математический анализ 8
2.1.1 Теоремы Вейерштрасса. 8
2.1.2 Теоремы Роля, Лагранжа. 8
2.1.3 Теоремы Коши, Ферма. 9
2.1.4 Формула Тейлора. 10
2.1.5 Длина гладкой кривой. 11
2.1.6 Объем тела вращения. 13
2.1.7 Площадь поверхности тела вращения. 14
2.1.8 Понятие компакта. 16
2.1.9 Необходимые и достаточные условия локальных экстремумов. 17
2.1.10 Задачи на относительный экстремум. Правило множителей Лагранжа. 18
2.1.11 Теорема о замене переменных в кратных интегралах. Полярные, цилиндрические и сферические системы координат. Геометрический смысл Якобиана. 20
2.1.12 Потенциальные векторные поля. Критерии потенциального векторного поля. 23
2.1.13 Формула Грина. 24
2.1.14 Формула Гаусса–Остроградского. 25
2.1.15 Формула Стокса. 26
2.2 Математическое моделирование, математическое программирование, теория игр, численные методы. 29
2.2.1 Регрессионная модель. Однофакторная модель (построение модели, определение дисперсии, проверка адекватности) 29
2.2.2 Двойственная задача линейного программирования. 31
2.2.3 Производственная функция Кобба-Дугласа. Коэффициенты эластичности. 34
2.2.4 Модели расчета годовой производственной программы. Критерии в моделях. 35
2.2.5 Модель оптимальной загрузки оборудования для выпуска комплектной продукции. Виды комплектов. 37
2.2.6 Математическая обработка результатов опытов в планировании эксперимента. Полный факторный эксперимент. Свойства матрицы планирования. 38
2.2.7 Управление запасами материалов. Типы моделей. Простейшая модель Уилсона. 41
2.2.8 Сетевые графики. Критический путь. Оптимизация графика по времени в зависимости от вложенных средств. 42
2.2.9 Сетевые графики. Вероятностная сеть. Оценка времени выполнения работ. 45
2.2.10 Динамическое программирование. Распределение ресурсов между предприятиями головной фирмы. 47
2.2.11 Задачи раскроя материалов и составления смеси. Область применения. 50
2.2.12 Транспортная задача. Закрытая транспортная задача. 53
2.2.13 Открытая транспортная задача. 55
2.2.14 Матричные игры. Игры  и
и  ............. 58
............. 58
2.2.15 Матричные игры  и линейное программирование. 62
и линейное программирование. 62
2.2.16 Методы решения нелинейных уравнений. 65
2.2.17 Методы решения систем линейных уравнений. 72
2.2.18 Нахождение наибольшего по модулю собственного числа матрицы. 77
2.2.19 Полиномиальное интерполирование. 78
2.2.20 Метод наименьших квадратов. 81
2.2.21 Численное интегрирование. 84
Список литературы. 86
ВВЕДЕНИЕ
Целью итоговой государственной аттестации является установление уровня подготовки студента к выполнению профессиональных задач и соответствия его подготовки требованиям государственного стандарта по данной специальности.
К итоговым аттестационным испытаниям допускаются лица, успешно завершившие в полном объеме освоение основной образовательной программы по специальности.
По специальности «Прикладная математика» для квалификации «дипломированный специалист» итоговая аттестация содержит формы: дипломная работа и государственный экзамен.
Итоговый экзамен проводится в форме итогового междисциплинарного экзамена по дисциплинам: математический анализ, математическое моделирование, методы оптимизации (математическое программирование), теория игр, численные методы.
Настоящее пособие содержит программу государственных экзаменов и методические указания по подготовке к экзаменам.
Перед работой с методическими указаниями необходимо проработать соответствующий лекционный материал и просмотреть набор задач, относящийся к данной теме.
ПРОГРАММА ГОСУДАРСТВЕННЫХ ЭКЗАМЕНОВ
Математический анализ
1. Теоремы Вейерштрасса.
2. Теоремы Роля, Лагранжа.
3. Теоремы Коши, Ферма.
4. Формула Тейлора.
5. Длина гладкой кривой.
6. Объем тела вращения.
7. Площадь поверхности тела вращения.
8. Понятие компакта.
9. Необходимые и достаточные условия локальных экстремумов.
10. Задачи на относительный экстремум. правило множителей Лагранжа.
11. Теорема о замене переменных в кратных интегралах. Полярные, цилиндрические и сферические системы координат. Геометрический смысл Якобиана.
12. Потенциальные векторные поля. Критерии потенциального векторного поля.
13. Формула Грина.
14. Формула Гаусса–Остроградского.
15. Формула Стокса.
Дата: 2018-12-28, просмотров: 384.