(Equivalent annual annuity, EAA)
Метод цепочки замещения не очень удобен в тех случаях, когда для уравнивания продолжительности проектов нужно повторять их много раз. В этом случае мы можем использовать метод эквивалентного годового аннуитета. Мы исходим из предположения, что если повторять оба проекта бесконечное число раз, то их продолжительности уравняются. Бесконечное повторение проектов даст в результате серию промежуточных выплат в размере NPV, которые будут бесконечными. Следующий шаг в анализе — предположить, что каждый платеж - это просто настоящая стоимость бесконечного аннуитета, которая накапливается в течение срока реализации проекта. Можно вычислить ЕАА из:
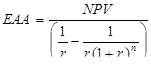(8.12)
Здесь r — ставка дисконта, а n — срок жизни проекта.
Поскольку мы уже превратили все промежуточные NPV в годовые аннуитеты, мы можем найти приведенную стоимость бесконечно повторяющихся проектов по формуле бесконечного аннуитета.
(8.13)
Теперь мы можем сравнить настоящие стоимости разных проектов и выбрать проект с максимальным значением NPV.
Пример 22: Применить метод EAA для оценки двух проектов из примера 20.
Находим значения EAA и NPV для первого проекта:
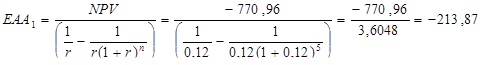тыс.руб.
NPV1(EAA метод) =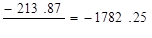 
тыс.руб.
Аналогично находим EAA и NPV для второго проекта:
EAA2 = -221,48 тыс.руб. NPV2(EAA метод) = -1845,70 тыс.руб.
Сравнение NPV двух проектов по методу ЕАА показывает, что по проекту 1 (покупка новой машины) NPV выше, его и следует выбрать.
Оценка риска
Проект - это инвестиции в реальные активы, которые порождают серию денежных потоков в будущем. Ранее, рассуждая об оценке будущих денежных потоков по проекту, мы предполагали, что денежные потоки детерминированы. Но в реальной жизни денежные потоки - это только оценка будущих последствий случайных событий. Исходя из этого, можно сказать, что риск проекта - это переменная ожидаемых денежных потоков, порожденных этим проектом. Далее мы обсудим различные методы, которые можно использовать при оценке риска ожидаемых денежных потоков по проекту.
Анализ чувствительности
Анализ чувствительности - это самый простой из всех методов оценки риска проектов. В этом методе мы предполагаем, что имеется одна критическая переменная, изменение которой вызовет все изменения денежных потоков по проекту. Некоторые из возможных кандидатов на роль такой переменной — число единиц проданной продукции, цена за единицу, удельные затраты и т.д. Проиллюстрируем метод анализа чувствительности на следующем примере.
Пример 23: Торговая продовольственная компания рассматривает проект создания собственной пекарни. Ниже приведены важнейшие параметры проекта.
Начальный денежный поток $100000
Продолжительность 5 лет
Ожидаемая цена продукции $0,75
Переменные затраты на единицу $0,25
Постоянные затраты (в год) $10000
Ставка налогообложения 30 %
Терминальная стоимость проекта отсутствует. Ожидается, что средний спрос на продукцию пекарни непредсказуем. Руководство ожидает, что ежегодный объем продаж может меняться, и разработало следующие сценарии:
Состояние экономики Вероятность Объем продаж
Отличное 0,3 130000
Среднее 0,5 100000
Плохое 0,2 70000
Провести анализ чувствительности и рассчитать ожидаемую NPV и стандартное отклонение ожидаемой NPV.
В данном примере ключевая переменная — это объем продаж. Прежде всего, рассчитаем ожидаемую NPV по всем трем возможным сценариям. В данном примере единственный компонент денежного потока проекта, который будет меняться — операционный денежный поток. Рассчитаем сначала операционный денежный поток, а затем используем его для оценки ожидаемой NPV.
Состояние экономики Отличное Среднее Плохое
Объем продаж 130000 100000 70000
Выручка от продаж (цена ´ объем) $97500 $75000 $52500
Переменные затраты (затраты ´ объем) -$32500 -$25000 -$17500
Постоянные затраты -$10000 -$10000 -$10000
Операционный доход до уплаты налогов $55000 $40000 $25000
Налог (30 %) -$16500 -$12000 -$ 7500
Чистый операционный денежный поток $38500 $28000 $17500
Налоговый щит за год составит: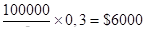 
в год
Теперь можем рассчитать NPV проекта для возможных состояний экономики:
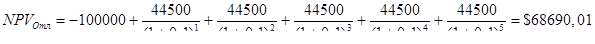
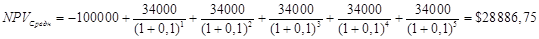
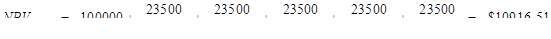
Ожидаемая NPV:
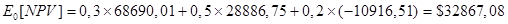
Рискованность проекта измеряется стандартным отклонением NPV:
sE[NPV] = [0,3 (68690,01–32867,08)2 + 0,5 (28886,75–32867,08)2 + 0,2 (–10916,51–32867,08)2]1/2 = 27862,23
Когда известна оценка ожидаемой чистой стоимости и ее стандартное отклонение, фирма может оценить вероятность убыточности проекта, чтобы принять решение о том, браться ли за его реализацию.
Приведенная в конце данной главы в Справочных материалах Таблица показывает пространство нормального распределения, т.е. Х стандартных отклонений влево и вправо от среднего (ожидаемого) значения анализируемого параметра – в данном случае параметра NPV при оценке нормального инвестиционного проекта.
Если принять, что распределение вероятностей в течение реализации проекта нормально, то можно рассчитать вероятность отрицательного значения NPV. Эта вероятность находится путем определения площади, лежащей слева под кривой от нулевой точки.
При нормальном распределении 2/3 распределения попадают в область, ограниченную одним стандартным отклонением в ту или иную сторону от ожидаемого значения параметра, т.е. в нашем случае с вероятностью 2/3 NPV будет находиться в пределах ± стандартное отклонение ожидаемой NPV.
2/3 площади
 | |||
| | |||
1/6 площади 1/6 площади
 |  |
NPV<0
Левый хвост Правый хвост
0 sE[NPV] E0 [ NPV] sE[NPV]
Рис. 8.2. Вероятностное распределение NPV проекта
Для начала необходимо вычислить разницу между критическим значением оцениваемого параметра и его ожидаемым значением.
В общем случае:
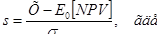Х – результат, в котором мы заинтересованы
В нашем случае критическим считается нулевое значение NPV*, поскольку проект отвергается при NPV ≤ 0, соответственно, разница будет как раз равна значению E0[NPV]. Затем нужно пронормировать эту разницу, разделив ее на стандартное отклонение NPV:
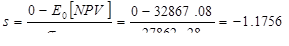
Полученный результат говорит о том, что критическое значение NPV находится на s-расстоянии стандартного отклонения от ожидаемого значения NPV. Следующий шаг – найти в таблице нормального распределения соответствующее значение s в левом столбце (число стандартных отклонений от среднего Х) и определить в правом столбце площадь влево или вправо (один хвост). Это и есть показатель вероятности того, что реализация проекта приведет к убыткам.
Для нашего проекта вероятность убытков составляет около 12%. Насколько высок риск реализации данного проекта решает менеджмент или собственник компании, исходя из своих представлений о соотношении доходности и риска.
Обычное правило заключается в том, чтобы одобрить проект с положительной чистой стоимостью, если уровень риска не выходит за пределы, установленные фирмой. Ниже мы рассмотрим, как фирмы устанавливают допустимый уровень риска.
Сценарный анализ
В анализе чувствительности мы допускали изменение только одной ключевой переменной. Но в реальной жизни денежные потоки по проекту зависят более чем от одной переменной. При сценарном анализе мы создаем несколько возможных сценариев, в которых изменяются более одной переменной, и приписываем каждому из них определенную вероятность. Затем мы оцениваем чистую стоимость по каждому сценарию и вычисляем ожидаемую NPV и стандартное отклонение NPV.
Пример 24: Продолжим рассмотрение проекта создания пекарни. Финансовый директор компании рассматривает три сценария для разных состояний экономики.
Сценарий 1 Сценарий 2 Сценарий 3
Начальный денежный поток $100000 $100000 $100000
Продолжительность проекта 5 лет 5 лет 5 лет
Ожидаемая продажная цена
за единицу продукции 0,85 $0,75 $0,60
Объем продаж, ед. 130000 100000 70000
Переменные затраты на ед. $0,20 $0,25 $0,30
Постоянные затраты (в год) $10000 $10000 $10000
Ставка налога для фирмы 30 % 30 % 30 %
Провести сценарный анализ проекта и рассчитать ожидаемую NPV и стандартное отклонение NPV.
Как и при анализе чувствительности, мы будем оценивать денежные потоки по каждому сценарию и после этого вычислим ожидаемую NPV проекта. Поскольку начальные денежные потоки и налоговые щиты по всем проектам одинаковы, мы пересчитаем только операционные денежные потоки.
Операционные денежные потоки:
Сценарий 1 Сценарий 2 Сценарий 3
Объем продаж 130000 100000 70000
Доход от продаж
(цена ´ объем) $110500 $75000 $42000
Переменные затраты
(затраты ´ объем) -$ 26000 -$25000 -$21000
Постоянные затраты $ 10000 -$10000 -$10000
Операционный
доход до уплаты налогов $ 74500 $40000 $11000
Налог на доход 30% -$22350 - $12000 -$ 3300
Чистый операционный
денежный поток $52150 $28000 $ 7700
Совокупный денежный поток по трем сценариям составит:
Год Сценарий 1 Сценарий 2 Сценарий 3
0 -$100000 -$100000 -$100000
1-5 +$ 58150 +$ 34000 +$ 13700
Зная совокупный денежный поток, мы можем рассчитать NPV:
NPV
Сценарий 1 +$110434,25
Сценарий 2 +$ 28886,75
Сценарий 3 - $ 48066,22
Ожидаемая чистая приведенная стоимость проекта составит:
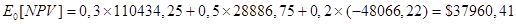
Риск проекта измеряется стандартным отклонением NPV:
EE[NPV] = [0,3 (110434,25 – 37960,41)2 + 0,5 (28886,75 – 37960,41)2 +
+ 0,2 (-48066,22 – 37960,71)2]1/2 = $ 55650,960
Рассчитаем теперь вероятность убыточности проекта:
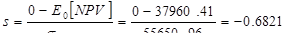
В таблице нормального распределения находим соответствующее значение вероятности – около 0,25, т.е. с вероятностью 25% реализация проекта принесет убытки.
Сравнивая результаты анализа чувствительности и сценарного анализа, мы видим, что ожидаемая NPV и стандартное отклонение NPV выше при сценарном анализе. Причина кроется в том, как создаются сценарии. Когда они строились, в оптимистическом прогнозе рассматривались все наиболее благоприятные показатели, а пессимистический прогноз предусматривал плохие значения всех показателей. Это приводит к более высокому стандартному отклонению NPV проекта по сценарному анализу.
Поправка на риск
Ранее, при обсуждении риска и доходности, мы обнаружили, что инвесторы ожидают более высокой доходности от вложений, связанных с большим риском. Тот же принцип можно применить и при оценке проектов, связанных с риском. Ставка дисконта в методе NPV есть средневзвешенная стоимость капитала по проекту. Если проект имеет более высокий риск, инвесторы будут ожидать более высокого дохода, что в свою очередь повысит стоимость капитала. При оценке проектов с разным уровнем риска возможно применение разных ставок дисконта.
В данном случае можно опереться только на иностранный опыт, так как российская рыночная практика еще не дает возможностей для обобщений. Берем требуемые нормы из американского опыта:
ü Инвестиции в повышение эффективности (снижение затрат, замена оборудования, перемещение производств в другие регионы) – 6-12 %
ü Инвестиции в расширение производства – ранее сформированные рынки, известные товары – 15-20%
ü Инвестиции в новые производства – новые рынки, новые товары – 25 %
ü Вынужденные инвестиции – требования закона, например, экологические, стандарты качества, лицензирования и т.д. – 0 %.
Варианты будущих решений
Метод NPV, традиционно используемый для оценки проектов, имеет один существенный недостаток — он не принимает в расчет возможных изменений деятельности в будущем. Проиллюстрируем это на следующем примере.
Пример 25: Фармацевтическая компания разрабатывает новый антибиотик, который можно будет использовать против всех известных бактерий. Фирма хочет вложить $1млн. в предварительные исследования, которые могут привести к выявлению молекулы, способной победить бактерии, для дальнейшего производства лекарства. Вероятность того, что эта молекула будет найдена в результате начальных исследований, составляет 50%. Начальная стадия предположительно продлится один год. В случае успеха на этом, начальном, этапе фирма может вложить еще $10 млн. в проверку лекарства на людях. Это может потребовать ещё один год, вероятность успеха составит 40 %. В случае успеха фирма может начать реальное производство лекарства, инвестировав в него еще $50 млн.
Фирме известно, что и другие компании ведут подобные исследования. Если фирма первой выйдет на рынок с новым лекарством, она займет монопольное положение на рынке и может получать ежегодный чистый денежный поток в размере $30 млн. (включая налоговый щит после уплаты налогов) в течение десяти лет. Если другие фирмы выйдут на рынок с подобным лекарством раньше нашей фирмы, то ожидаемый годовой чистый денежный поток составит лишь $5млн. Фирма считает, что вероятность разработки лекарства другими фирмами составляет 40%. Если стоимость капитала по проекту 10%, какова ожидаемая NPV проекта?
Фирме необходимо принять несколько последовательных решений. Вот последовательность доходов и расходов по проекту.
Год 0 Год 1 Год 2 Год 3 Год 10
0,6 $30млн. $30млн
-$50млн.
0,4
0,4 $5млн. $5млн.
-$10млн.
0,5
0,6 0
-$1млн.
0,5 0
Мы видим, что в проекте существует четыре возможности выхода из проекта и каждую из них можно рассматривать как сценарий. Ниже приводятся совместные вероятности и приведенные чистые стоимости (NPV) по каждому из этих четырех сценариев.
Совместная вероятность NPV
Сценарий 1 0,5´0,4´0,6 = 0,12 $100,9314млн.
Сценарий 2 0,5´0,4´0,4 = 0,08 -$26,0224 млн.
Сценарий 3 0,5´0,6 = 0,30 -$10,0909 млн.
Сценарий 4 0,5 = 0,50 -$ 1,0000 млн.
Ожидаемая NPV проекта равна:
E0[NPV] = 0,12´100,9314 – 0,8 ´ 26,0224 – 0,3´10,0909 – 0,5´1 = $6,5027 млн.
В приведенном примере у фирмы есть опцион, возможность или право прекратить проект, если условия складываются неблагоприятно. Представьте, какие убытки фирма могла бы понести, если бы она решила инвестировать все средства сразу, не ожидая результатов каждой фазы проекта!
Реальные опционы можно определить как право предпринять определенные действия в определенный момент времени. Приведем еще несколько примеров опционов, права действий по определенным проектам:
- Фирма, занимающаяся бурением нефтяных скважин, может прекратить добычу нефти из скважины, если цена на нефть снизится.
- Электростанция может переключиться с природного газа на нефть, если цена на природный газ вырастет.
- Производитель автомобилей может временно закрыть сборочный завод в случае падения спроса на автомобили.
- Производитель компьютеров может быстро перевести сборочный конвейер на изготовление другого вида компьютеров, если меняется рыночный спрос.
Традиционный метод расчета NPV, в котором просто дисконтируются будущие денежные потоки, не может учесть стоимость опционов, потому что их стоимость зависит от событий, которые произойдут в будущем. Их можно оценить с помощью моделей оценки опционов, которые мы в данной книге не рассматриваем.
Выводы
Планирование капитальных вложений — одна из самых важных тем в управлении финансами. Будущая доходность фирмы зависит от тех решений о вложении средств в реальные активы, которые она примет сегодня. В данной главе мы рассмотрели различные методы оценки проектов. Определение чистой приведенной стоимости NPV – это наиболее подходящий метод оценки проектов.
Поскольку оценка проекта зависит от будущих денежных потоков по нему, абсолютно необходимо как можно точнее оценить эти денежные потоки. Наилучший способ для этого — оценить приращение денежных потоков, т.е. разницу между денежными потоками фирмы с учетом реализации проекта и без этого проекта
Денежные потоки по проекту ожидаются в будущем, которое всегда неопределенно, следовательно, фирма должна принимать в расчет фактор риска, связанный с инвестиционным проектом. Есть разные способы оцени риска проекта, и мы обсудили два — анализ чувствительности и сценарный анализ.
Реально каждый проект связан с определенными возможностями выбора в будущем (опционами), которые зависят от результатов реализации отдельных фаз проекта и направлены на улучшение общих результатов проекта.
Контрольные вопросы по теме «Планирование капиталовложений»
1. Почему инвестиционные решения по взаимоисключающим и независимым проектам принимаются по-разному?
2. Проекты замещения и новые инвестиционные проекты – в чем состоит их различие? Отражается ли это при оценке проекта? Каким именно образом?
3. Почему оценка инвестиционных проектов методом расчета дисконтированного срока окупаемости может привести к принятию неверного решения?
4. По какой ставке дисконтирования фирмы оценивают инвестиционные проекты? Каким образом при этом можно учитывать рискованность оцениваемых проектов?
5. Какие из методов оценки инвестиционных проектов могут давать неверные решения и по каким причинам?
6. Почему критерий IRR (внутренняя норма доходности проекта) называют иногда барьерной ставкой. Какая связаны критерии IRR и запас прочности проекта?
7. В чем суть конфликта методов оценки инвестиционных проектов? Какие методы "конфликтуют"? Дайте не менее двух интерпретаций.
8. Почему фирмы иногда используют ставку Cr (точку Фишера) для принятия инвестиционного решения при выборе из двух взаимоисключающих проектов? От оценки проектов какими методами они при этом отказываются?
9. Какой из методов оценки инвестиционных проектов снимает противоречия двух других методов? В чем состоит основная идея этого метода?
10. Какой из методов оценки инвестиционных проектов признается наиболее универсальным? Однако и этот метод не лишен определенной ограниченности. В чем она состоит?
11. Какой из критериев оценки инвестиционных проектов является аналогом доходности к погашению при оценке облигации?
12. Какие приемы применяются при оценке проектов разной продолжительности? Опишите не менее двух способов.
13. Почему и как внешние эффекты должны включаться в анализ эффективности намечаемых капиталовложений? Приведите пример внешних эффектов.
14. Какие денежные потоки формируют денежный поток по инвестиционному проекту?
15. Охарактеризуйте способы учета риска инвестиционного проекта. Опишите не менее двух способов.
16. В чем сущность опциона? Приведите пример реального опциона (связанного с инвестиционным проектом). Можно ли измерить стоимость опциона?
Справочные материалы по теме:
Таблица нормального распределения
| Число стандартных отклонений от среднего (Х) | Площадь влево или вправо (один хвост) | Число стандартных отклонений от среднего (Х) | Площадь влево или вправо (один хвост) |
| 0,00 | 0,5000 | 1,55 | 0,0606 |
| 0,05 | 0,4801 | 1,60 | 0,0548 |
| 0,10 | 0,4602 | 1,65 | 0,0495 |
| 0,15 | 0,4404 | 1,70 | 0,0446 |
| 0,20 | 0,4207 | 1,75 | 0,0401 |
| 0,25 | 0,4013 | 1,80 | 0,0359 |
| 0,30 | 0,3821 | 1,85 | 0,0322 |
| 0,35 | 0,3632 | 1,90 | 0,0287 |
| 0,40 | 0,3446 | 1,95 | 0,0256 |
| 0,45 | 0,3264 | 2,00 | 0,0228 |
| 0,50 | 0,3085 | 2,05 | 0,0202 |
| 0,55 | 0,2912 | 2,10 | 0,0179 |
| 0,60 | 0,2743 | 2,15 | 0,0158 |
| 0,65 | 0,2578 | 2,20 | 0,0139 |
| 0,70 | 0,2420 | 2,25 | 0,0122 |
| 0,75 | 0,2264 | 2,30 | 0,0107 |
| 0,80 | 0,2119 | 2,35 | 0,0094 |
| 0,85 | 0,1977 | 2,40 | 0,0082 |
| 0,90 | 0,1841 | 2,45 | 0,0071 |
| 0,95 | 0,1711 | 2,50 | 0,0062 |
| 1,00 | 0,1577 | 2,55 | 0,0054 |
| 1,05 | 0,1469 | 2,60 | 0,0047 |
| 1,10 | 0,1357 | 2,65 | 0,0040 |
| 1,15 | 0,1251 | 2,70 | 0,0035 |
| 1,20 | 0,1151 | 2,75 | 0,0030 |
| 1,25 | 0,1056 | 2,80 | 0,0026 |
| 1,30 | 0,0968 | 2,85 | 0,0022 |
| 1,35 | 0,0885 | 2,90 | 0,0019 |
| 1,40 | 0,0808 | 2,95 | 0,0016 |
| 1,45 | 0,0735 | 3,00 | 0,013 |
| 1,50 | 0,0668 |
Список литературы
1. Бригхэм Юджин Ф. Энциклопедия финансового менеджмента: краткий курс; Пер. с англ. / Ю.Ф.Бригхэм, Дж.Хьюстон – 4-е изд. Спб.: Питер, 2007.
2. Бригхэм, Юджин Ф. Финансовый менеджмент : учебник: пер. с англ. / Ю. Ф. Бригхэм, М. С. Эрхаррдт ; Ред. Е. А. Дорофеев. - 10-е изд. - СПб. : Питер, 2005.
3. Грей, Клиффорд Ф. Управление проектами : учебник: пер. с англ. / К. Ф. Грей, Э. У. Ларсон. - 3-е изд., полн. перераб. - М. : Дело и сервис, 2007.
4. Ван Хорн Дж. К., Вахович Дж. Основы управления финансами / Пер. с англ. – М.: Финансы и статистика, 2009.
5. Дж.К.Шим, Дж.Г.Сигел. Финансовый менеджмент. М., Экономика для практиков, 1996, с. 141-153, 173-182
6. Шим Дж.К., Сигел Дж.Г. Основы коммерческого бюджетирования. СПб, 1998.
7. Ковалев В.В. Введение в финансовый менеджмент: Учебник для вузов. – М.: Финансы и статис-
тика. 2006.
8. Лапуста М.Г., Скамай Л.Г. Финансы фирмы: Учеб. пособие – М.: ИНФРА-М, 2002 (Серия «Вопрос – ответ»)
9. Модильяни Ф., Миллер М. Сколько стоит фирма? Теорема ММ: Пер. с англ. – М.: Дело, 2001
10. Ершов Ю.С. Финансовая математика в вопросах и ответах. Учебное пособие. – Новосибирск: Сибирское соглашение, 1999
11. Финансовый менеджмент: теория и практика: Учебник / Под ред. Е.С.Стояновой. – 6-е изд. - М.: Изд-во "Перспектива", 2010.
ТАБЛИЦА С-1. Текущая стоимость $1 за период 
| 1,00% | 1,25% | 1,50% . | 1,75% | 2,00% | 3,00% | 4 ,00% | 5,00% | 6,00% | 7,00% | 8,00% | 9,00% | 10,00% | 12,00% | 14,00% | 15,00% | |
| 1 | 0,9901 | 0,9877 | 0,9852 | 0,9828 | 0,9804 | 0,9709 | 0,9615 | 0,9524 | 0,9434 | 0,9346 | 0,9259 | 0,9174 | 0,9091 | 0,8929 | 0,8772 | 0,8696 |
| 2 | 0,9803 | 0,9755 | 0,9707 | 0,9659 | 0,9612 | 0,9426 | 0,9246 | 0,9070 | 0,8900 | 0,8734 | 0,8573 | 0,8417 | 0,8264 | 0,7972 | 0,7695 | 0,7561 |
| 3 | 0,9706 | 0,9634 | 0,9563 | 0,9493 | 0,9423 | 0,9151 | 0,8890 | 0,8638 | 0,8396 | 0,8163 | 0,7938 | 0,7722 | 0,7513 | 0,7118 | 0,6750 | 0,6575 |
| 4 | 0,9610 | 0,9515 | 0,9422 | 0,9330 | 0,9238 | 0,8885 | 0,8548 | 0,8227 | 0,7921 | 0,7629 | 0,7350 | 0,7084 | 0,6830 | 0,6355 | 0,5921 | 0,5718 |
| 5 | 0,9515 | 0,9398 | 0,9283 | 0,9169 | 0,9057 | 0,8626 | 0,8219 | 0,7835 | 0,7473 | 0,7130 | 0,6806 | 0,6499 | 0,6209 | 0,5674 | 0,5194 | 0,4972 |
| 6 | 0,9420 | 0,9282 | 0,9145 | 0,9011 | 0,8880 | 0,8375 | 0,7903 | 0,7462 | 0,7050 | 0,6663 | 0,6302 | 0,5963 | 0,5645 | 0,5066 | 0,4556 | 0,4323 |
| 7 | 0,9327 | 0,9167 | 0,9010 | 0,8856 | 0,8706 | 0,8131 | 0,7599 | 0,7107 | 0,6651 | 0,6227 | 0,5835 | 0,5470 | 0,5132 | 0,4523 | 0,3996 | 0,3759 |
| 8 | 0,9235 | 0,9054 | 0,8877 | 0,8704 | 0,8535 | 0,7894 | 0,7307 | 0,6768 | 0.6274 | 0,5820 | 0,5403 | 0,5019 | 0,4665 | 0,4039 | 0,3506 | 0,3269 |
| 9 | 0,9143 | 0,8942 | 0,8746 | 0,8554 | 0,8368 | 0,7664 | 0,7026 | 0,6446 | 0,5919 | 0,5439 | 0,5002 | 0,4604 | 0,4241 | 0,3606 | 0,3075 | 0,2843 |
| 10 | 0,9053 | 0,8832 | 0,8617 | 0,8407 | 0,8203 | 0,7441 | 0,6756 | 0,61391 | 0,5584 | 0,5083 | 0,4632 | 0,4224 | 0,3855 | 0,3220 | 0,2697 | 0,2472 |
| 11 | 0,8963 | 0,8723 | 0,8489 | 0,8263 | 0,8043 | 0.7224 | 0,6496 | 0,5847 | 0,5268 | 0,4751 | 0,4289 | 0,3875 | 0,3505 | 0,2875 | 0,2366 | 0,2149 |
| 12 | 0,8874 | 0,8615 | 0,8364 | 0,8121 | 0,7885 | 0,7014 | 0,6246 | 0,5568 | 0,4970 | 0,4440 | 0,3971 | 0,3555 | 0,3186 | 0,2567 | 0,2076 | 0,1869 |
| 13 | 0,8787 | 0,8509 | 0,8240 | 0,7981 | 0,7730 | 0,6810 | 0,6006 | 0,5303 | 0,4688 | 0,4150 | 0,3677 | 0,3262 | 0,2897 | 0,2292 | 0,1821 | 0,1625 |
| 14 | 0,8700 | 0,8404 | 0,8118 | 0,7844 | 0,7579 | 0,6611 | 0,5775 | 0,5051 | 0,4423 | 0,3878 | 0,3405 | 0,2992 | 0,2633 | 0,2046 | 0,1597 | 0,1413 |
| 15 | 0,8613 | 0,8300 | 0,7999 | 0,7709 | 0,7430 | 0,6419 | 0,5553 | 0,4810 | 0,4173 | 0,3624 | 0,3152 | 0,2745 | 0,2394 | 0,1827 | 0,1401 | 0,1229 |
| 16 | 0,8528 | 0,8197 | 0,7880 | 0,7576 | 0,7284 | 0,6232 | 0,5339 | 0,4581 | 0,3936 | 0,3387 | 0,2919 | 0,2519 | 0,2176 | 0,1631 | 0,1229 | 0,1069 |
| 17 | 0,8444 | 0,8096 | 0,7764 | 0,7446 | 0,7142 | 0,6050 | 0,5134 | 0,4363 | 0,3714 | 0,3166 | 0,2703 | 0,2311 | 0,1978 | 0,1456 | 0,1078 | 0,0929 |
| 18 | 0,8360 | 0,7996 | 0,7649 | 0,7318 | 0,7002 | 0,5874 | 0,4936 | 0,4155 | 0,3503 | 0,2959 | 0,2502 | 0,2120 | 0,1799 | 0,1300 | 0,0946 | 0,0808 |
| 19 | 0,8277 | 0,7898 | 0,7536 | 0,7192 | 0,6864 | 0,5703 | 0,4746 | 0,3957 | 0,3305 | 0,2765 | 0,2317 | 0,1945 | 0,1635 | 0,1161 | 0,0829 | 0,0703 |
| 20 | 0,8195 | 0,7800 | 0,7425 | 0,7068 | 0,6730 | 0,5537 | 0,4564 | 0,3769 | 0,3118 | 0,2584 | 0,2145 | 0,1784 | 0,1486 | 0,1037 | 0,0728 | 0,0611 |
| 21 | 0,8114 | 0,7704 | 0,7315 | 0,6947 | 0,6598 | 0,5375 | 0,4388 | 0,3589 | 0,2942 | 0,2415 | 0,1987 | 0,1637 | 0,1351 | 0,0926 | 0,0638 | 0,0531 |
| 22 | 0,8034 | 0,7609 | 0,7207 | 0,6827 | 0,6468 | 0,5219 | 0,4220 | 0,3418 | 0,2775 | 0,2257 | 0,1839 | 0,1502 | 0,1228 | 0,0826 | 0,0560 | 0,0462 |
| 23 | 0,7954 | 0,7515 | 0,7100 | 0,6710 | 0,6342 | 0,5067 | 0,4057 | 0,3256 | 0,2618 | 0,2109 | 0,1703 | 0,1378 | 0,1117 | 0,0738 | 0,0491 | 0,0402 |
| 24 | 0,7876 | 0,7422 | 0,6995 | 0,6594 | 0,6217 | 0,4919 | 0,3901 | 0,3101 | 0,2470 | 0,1971 | 0,1577 | 0,1264 | 0,1015 | 0,0659 | 0,0431 | 0,0349 |
| 25 | 0,7798 | 0,7330 | 0,6892 | 0,6481 | 0,6095 | 0,4776 | 0,3751 | 0,2953 | 0,2330 | 0,1842 | 0,1460 | 0,1160 | 0,0923 | 0,0588 | 0,0378 | 0,0304 |
| 26 | 0,7720 | 0,7^40 | 0,6790 | 0,6369 | 0,5976 | 0,4637 | 0,3607 | 0,2812 | 0,2198 | 0,1722 | 0,1352 | 0,1064 | 0,0839 | 0,0525 | 0,0331 | 0,0264 |
| 27 | 0,7644 | 0,7150 | 0,6690 | 0,6260 | 0,5859 | 0,4502 | 0,3468 | 0,2678 | 0,2074 | 0,1609 | 0,1252 | 0,0976 | 0,0763 | 0,0469 | 0,0291 | 0,0230 |
| 28 | 0,7568 | 0,7062 | 0,6591 | 0,6152 | 0,5744 | 0,4371 | 0,3335 | 0,2551 | 0,1956 | 0,1504 | 0,1159 | 0,0895 | 0,0693 | 0,0419 | 0,0255 | 0,0200 |
| 29 | 0,7493 | 0,6975 | 0,6494 | 0,6046 | 0,5631 | 0,4243 | 0,3207 | 0,2429 | 0,1846 | 0,1406 | 0,1073 | 0,0822 | 0,0630 | 0,0374 | 0,0224 | 0,0174 |
| 30 | 0,7419 | 0,6889 | 0,6398 | 0,5942 | 0,5521 | 0,4120 | 0,3083 | 0,2314 | 0,1741 | 0,1314 | 0,0994 | 0,0754 | 0,0573 | 0,0334 | 0,0196 | 0,0151 |
ТАБЛИЦА С-2. Текущая стоимость аннуитета $1 за период 
| 1,00% | 1,25% | 1,50% | 1,75% | 2,00% | 3,00% | 4,00% | 5,00% | 6,00% | 7,00% | 8,00% | 9,00% | 10,00% | 12,00% | 14,00% | 15,00% | |
| 1 | 0,9901 | 0,9877 | 0,9852 | 0,9828 | 0,9804 | 0,9709 | 0,9615 | 0,9524 | 0,9434 | 0,9346 | 0,9259 | 0,9174 | 0,9091 | 0,8929 | 0,8772 | 0,8696 |
| 2 | 1,9704 | 1,9631 | 1,9559 | 1,9487 | 1,9416 | 1,9135 | 1,8861 | 1,8594 | 1,8334 | 1,8080 | 1,7833 | 1,7591 | 1,7355 | 1,6901 | 1,6467 | 1,6257 |
| 3 | 2,9410 | 2,9265 | 2,9122 | 2,8980 | 2,8839 | 2,8286 | 2,7751 | 2,7232 | 2,6730 | 2,6243 | 2,5771 | 2,5313 | 2,4869 | 2,4018 | 2,3216 | 2,2832 |
| 4 | 3,9020 | 3,8781 | 3,8544 | 3,8309 | 3,8077 | 3,7171 | 3,6299 | 3,5460 | 3,4651 | 3,3872 | 3,3121 | 3,2397 | 3,1699 | 3,0373 | 2,9137 | 2,8550 |
| 5 | 4,8534 | 4,8178 | 4,7826 | 4,7479 | 4,7135 | 4,5797 | 4,4518 | 4,3295 | 4,2124 | 4.1002 | 3,9927 | 3,8897 | 3,7908 | 3,6048 | 3,4331 | 3,3522 |
| 6 | 5,7955 | 5,7460 | 5,6972 | 5,6490 | 5,6014 | 5,4172 | 5,2421 | 5,0757 | 4,9173 | 4,7665 | 4,6229 | 4,4859 | 4,3553 | 4,1114 | 3,8887 | 3,7845 |
| 7 | 6,7282 | 6,6627 | 6,5982 | 6,5346 | 6,4720 | 6,2303 | 6,0021 | 5,7864 | 5,5824 | 5,3893 | 5,2064 | 5,0330 | 4,8684 | 4,5638 | 4,2883 | 4,1604 |
| 8 | 7,6517 | 7,5681 | 7,4859 | 7,4051 | 7,3255 | 7,0197 | 6,7327 | 6,4632 | 6,2098 | 5,9713 | 5,7466 | 5,5348 | 5,3349 | 4,9676 | 4,6389 | 4,4873 |
| 9 | 8,5660 | 8,4623 | 8,3605 | 8,2605 | 8,1622 | 7,7861 | 7,4353 | 7,1078 | 6,8017 | 6,5152 | 6,2469 | 5,9952 | 5,7590 | 5,3282 | 4,9464 | 4,7716 |
| 10 | 9,4713 | 9,3455 | .9,2222 | 9,1012 | 8,9826 | 8,5302 | 8,1109 | 7,7217 | 7,3601 | 7,0236 | 6,7101 | 6,4177 | 6,1446 | 5,6502 | 5,2161 | 5,0188 |
| 11 | 10,3676 | 10,2178 | 10,0711 | 9,9275 | 9,7868 | 9,2526 | 8,7605 | 8,3064 | 7,8869 | 7,4987 | 7,1390 | 6,8052 | 6,4951 | 5,9377 | 5,4527 | 5,2337 |
| 12 | 11,2551 | 11,0793 | 10,9075 | 10,7395 | 10,5753 | 9,9540 | 9,3851 | 8,8633 | 8,3838 | 7,9427 | 7,5361 | 7,1607 | 6,8137 | 6,1944 | 5,6603 | 5,4206 |
| 13 | 12,1337 | 11,9302 | 11,7315 | 11,5376 | 11.3484 | 10,6350 | 9,9856 | 9,3936 | 8,8527 | 8,3577 | 7,9038 | 7,4869 | 7,1034 | 6,4235 | 5,8424 | 5,5831 |
| 14 | 13,0037 | 12,7706 | 12,5434 | 12,3220 | 12,1062 | 11,2961 | 10,5631 | 9,8986 | 9,2950 | 8,7455 | 8,2442 | 7,7862 | 7,3667 | 6,6282 | 6,0021 | 5,7245 |
| 15 | 13,8651 | 13,6005 | 13,3432 | 13,0929 | 12,8493 | 11,9379 | 11,1184 | 10,3797 | 9,7122 | 9,1079 | 8,5595 | 8,0607 | 7,6061 | 6,8109 | 6,1422 | 5,8474 |
| 16 | 14,7179 | 14,4203 | 14,1313 | 13,8505 | 13.5777 | 12,5611 | 11,6523 | 10,8378 | 10,1059 | 9,4466 | 8,8514 | 8,3126 | 7,8237 | 6,9740 | 6,2651 | 5,9542 |
| 17 | 15,5623 | 15,2299 | 14,9076 | 14,5951 | 14,2919 | 13,1661 | 12,1657 | 11,2741 | 10,4773 | 9,7632 | 9,1216 | 8,5436 | 8,0216 | 7,1196 | 6,3729 | 6,0472 |
| 18 | 16,3983 | 16,0295 | 15,6726 | 15,3269 | 14,9920 | 13,7535 | 12,6593 | 11,6896 | 10,8276 | 10,0591 | 9,3719 | 8,7556 | 8,2014 | 7,2497 | 6,4674 | 6,1280 |
| 19 | 17,2260 | 16,8193 | 16,4262 | 16,0461 | 15,6785 | 14,3238 | 13,1339 | 12,0853 | 11,1581 | 10,3356 | 9,6036 | 8,9501 | 8,3649 | 7,3658 | 6,5504 | 6,1982 |
| 20 | 18,0456 | 17,5993 | 17,1686 | 16,7529 | 16,3514 | 14,8775 | 13,5903 | 12,4622 | 11,4699 | 10,5940 | 9,8181 | 9,1285 | 8,5136 | 7,4694 | 6,6231 | 6,2593 |
| 21 | 18,8570 | 18,3697 | 17,9001 | 17,4475 | 17,0112 | 15,4150 | 14,0292 | 12.8212 | 11,7641 | 10,8355 | 10,0168 | 9,2922 | 8,6487 | 7,5620 | 6,6870 | 6,3125 |
| 22 | 19,6604 | 19,1306 | 18,6208 | 18,1303 | 17,6580 | 15,9369 | 14,4511 | 13,1630 | 12,0416 | 11,0612 | 10,2007 | 9,4424 | 8,7715 | 7,6446 | 6,7429 | 6,3587 |
| 23 | 20,4558 | 19,8820 | 19,3309 | 18,8012 | 18,2922 | 16,4436 | 14,8568 | 13,4886 | 12,3034 | 11,2722 | 10.3711 | 9,5802 | 8,8832 | 7,7184 | 6,7921 | 6,3988 |
| 24 | 21,2434 | 20,6242 | 20.0304 | 19,4607 | 18,9139 | 16,9355 | 15,2470 | 13,7986 | 12,5504 | 11,4693 | 10,5288 | 9,7066 | 8,9847 | 7,7843 | 6,8351 | 6,4338 |
| 25 | 22,0232 | 21,3573 | 20,7196 | 20,1088 | 19,5235 | 17,4131 | 15,6221 | 14,0939 | 12,7834 | 11,6536 | 10,6748 | 9,8226 | 9,0770 | 7,8431 | 6,8729 | 6,4641 |
| 26 | 22,7952 | 22,0813 | 21,3986 | 20,7457 | 20,1210 | 17,8768 | 15,9828 | 14,3752 | 13,0032 | 11,8258 | 10,8100 | 9,9290 | 9,1609 | 7,8957 | 6,9061 | 6.4906 |
| 27 | 23,5596 | 22,7963 | 22,0676 | 21,3717 | 20,7069 | 18,3270 | 16,3296 | 14,6430 | 13.2105 | 11,9867 | 10,9352 | 10,0266 | 9,2372 | 7,9426 | 6,9352 | 6,5135 |
| 28 | 24,3164 | 23,5025 | 22,7267 | 21,9870 | 21,2813 | 18,7641 | 16,6631 | 14,8981 | 13,4062 | 12,1371 | 11,0511 | 10,1161 | 9,3066 | 7,9844 | 6,9607 | 6,5335 |
| 29 | 25,0658 | 24,2000 | 23.3761 | 22,5916 | 21,8444 | 19,1885 | 16,9837 | 15,1411 | 13,5907 | 12,2777 | 11,1584 | 10,1983 | 9,3696 | 8,0218 | 6,9830 | 6,5509 |
| 30 | 25,8077 | 24,8889 | 24,0158 | 23,1858 | 22,3965 | 19,6004 | 17,2920 | 15,3725 | 13,7648 | 12,4090 | 11,2578 | 10,2737 | 9,4269 | 8,0552 | 7,0027 | 6,5660 |
ТАБЛИЦА С-З. Будущая стоимость $1 за период 
| 1,00% | 1,25% | 1,50% | 1,75% | 2,00% | 3,00% | 4 ,00% | 5,00% | 6,00% | 7,00% | 8,00% | 9,00% | 10,00% | 12,00% | 14,00% | 15.00% | |
| 1 | 1,0100 | 1,0125 | 1,0150 | 1,0175 | 1,0200 | 1,0300 | 1,0400 | 1,0500 | 1,0600 | 1,0700 | 1,0800 | 1,0900 | 1,1000 | 1,1200 | 1,1400 | 1,1500 |
| 2 | 1,0201 | 1,0252 | 1,0302 | 1,0353 | 1,0404 | 1,0609 | 1,0816 | 1,1025 | 1,1236 | 1,1449 | 1,1664 | 1,1881 | 1,2100 | 1,2544 | 1,2996 | 1,3225 |
| 3 | 1,0303 | 1,0380 | 1,0457 | 1,0534 | 1,0612 | 1,0927 | 1,1249 | 1,1576 | 1,1910 | 1,2250 | 1,2597 | 1,2950 | 1,3310 | 1,4049 | 1,4815 | 1,5209 |
| 4 | 1,0406 | 1,0509 | 1,0614 | 1,0719 | 1,0824 | 1,1255 | 1,1699 | 1,2155 | 1,2625 | 1,3108 | 1,3605 | 1,4116 | 1,4641 | 1,5735 | 1,6890 | 1,7490 |
| 5 | 1,0510 | 1,0641 | 1,0773 | 1,0906 | 1,1041 | 1,1593 | 1,2167 | 1,2763 | 1,3382 | 1,4026 | 1,4693 | 1,5386 | 1,6105 | 1,7623 | 1,9254 | 2,0114 |
| 6 | 1,0615 | 1,0774 | 1.0934 | 1,1097 | 1,1262 | 1,1941 | 1,2653 | 1,3401 | 1,4185 | 1,5007 | 1,5869 | 1,6771 | 1,7716 | 1,9738 | 2,1950 | 2,3131 |
| 7 | 1,0721 | 1,0909 | 1,1098 | 1,1291 | 1,1487 | 1,2299 | 1,3159 | 1,4071 | 1,5036 | 1,6058 | 1,7138 | 1,8280 | 1,9487 | 2,2107 | 2,5023 | 2,6600 |
| 8 | 1,0829 | 1,1045 | 1,1265 | 1,1489 | 1,1717 | 1,2668 | 1,3686 | 1,4775 | 1,5938 | 1,7182 | 1,8509 | 1,9926 | 2,1436 | 2,4760 | 2,8526 | 3,0590 |
| 9 | 1,0937 | 1,1183 | 1,1434 | 1,1690 | 1,1951 | 1,3048 | 1,4233 | 1,5513 | 1,6895 | 1,8385 | 1,9990 | 2,1719 | 2,3579 | 2,7731 | 3,2519 | 3,5179 |
| 10 | 1,1046 | 1,1323 | 1,1605 | 1,1894 | 1,2190 | 1,3439 | 1,4802 | 1,6289 | 1,7908 | 1,9672 | 2,1589 | 2,3674 | 2,5937 | 3,1058 | 3,7072 | 4,0456 |
| 11 | 1,1157 | 1,1464 | 1,1779 | 1,2103 | 1,2434 | 1,3842 | 1,5395 | 1,7103 | 1,8983 | 2,1049 | 2,3316 | 2,5804 | 2,8531 | 3,4785 | 4,2262 | 4,6524 |
| 12 | 1,1268 | 1,1608 | 1,1956 | 1,2314 | 1,2682 | 1,4258 | 1,6010 | 1,7959 | 2,0122 | 2,2522 | 2,5182 | 2,8127 | 3,1384 | 3,8960 | 4,8179 | 5,3503 |
| 13 | 1,1381 | 1,1753 | 1,2136 | 1,2530 | 1,2936 | 1,4685 | 1,6651 | 1,8856 | 2,1329 | 2,4098 | 2,7196 | 3,0658 | 3,4523 | 4,3635 | 5,4924 | 6.1528 |
| 14 | 1,1495 | 1,1900 | 1,2318 | 1,2749 | 1,3195 | 1,5126 | 1,7317 | 1,9799 | 2,2609 | 2,5785 | 2,9372 | 3,3417 | 3,7975 | 4,8871 | 6,2613 | 7,0757 |
| 15 | 1,1610 | 1,2048 | 1,2502 | 1,2972 | 1,3459 | 1,5580 | 1,8009 | 2,0789 | 2,3966 | 2,7590 | 3,1722 | 3,6425 | 4,1772 | 5,4736 | 7,1379 | 8,1371 |
| 16 | 1,1726 | 1,2199 | 1,2690 | 1,3199 | 1,3728 | 1,6047 | 1,8730 | 2,1829 | 2,5404 | 2,9522 | 3,4259 | 3,9703 | 4,5950 | 6,1304 | 8,1372 | 9,3576 |
| 17 | 1,1843 | 1,2351 | 1,2880 | 1,3430 | 1,4002 | 1,6528 | 1,9479 | 2,2920 | 2,6928 | 3,1588 | 3,7000 | 4,3276 | 5,0545 | 6,8660 | 9,2765 | 10,7613 |
| 18 | 1,1961 | 1,2506 | 1,3073 | 1,3665 | 1,4282 | 1,7024 | 2,0258 | 2,4066 | 2,8543 | 3,3799 | 3,9960 | 4.7171 | 5,5599 | 7,6900 | 10,5752 | 12.3755 |
| 19 | 1,2081 | 1,2662 | 1,3270 | 1.3904 | 1,4568 | 1,7535 | 2,1068 | 2,5270 | 3,0256 | 3,6165 | 4,3157 | 5,1417 | 6,1159 | 8,6128 | 12,0557 | 14,2318 |
| 20 | 1,2202 | 1,2820 | 1,3469 | 1,4148 | 1,4859 | 1,8061 | 2,1911 | 2,6533 | 3,2071 | 3,8697 | 4,6610 | 5,6044 | 6,7275 | 9,6463 | 13,7435 | 16,3665 |
| 21 | 1,2324 | 1,2981 | 1,3671 | 1,4395 | 1,5157 | 1,8603 | 2,2788 | 2,7860 | 3,3996 | 4,1406 | 5,0338 | 6,1088 | 7,4002 | 10,8038 | 15,6676 | 18,8215 |
| 22 | 1,2447 | 1,3143 | 1,3876 | 1,4647 | 1,5460 | 1,9161 | 2,3699 | 2,9253 | 3,6035 | 4,4304 | 5,4365 | 6,6586 | 8,1403 | 12,1003 | 17,8610 | 21,6447 |
| 23 | 1,2572 | 1,3307 | 1,4084 | 1,4904 | 1,5769 | 1,9736 | 2,4647 | 3,0715 | 3,8197 | 4,7405 | 5,8715 | 7,2579 | 8,9543 | 13,5523 | 20,3616 | 24,8915 |
| 24 | 1,2697 | 1,3474 | 1,4295 | 1,5164 | 1,6084 | 2,0328 | 2,5633 | 3,2251 | 4,0489 | 5,0724 | 6,3412 | 7,9111 | 9,8497 | 15,1786 | 23,2122 | 28,6252 |
| 25 | 1,2824 | 1,3642 | 1,4509 | 1,5430 | 1,6406 | 2,0938 | 2,6658 | 3,3864 | 4,2919 | 5,4274 | 6,8485 | 8,6231 | 10,8347 | 17,0001 | 26,4619 | 32,9190 |
| 26 | 1,2953 | 1,3812 | 1,4727 | 1,5700 | 1,6734 | 2,1566 | 2,7725 | 3,5557 | 4,5494 | 5,8074 | 7,3964 | 9,3992 | 11,9182 | 19,0401 | 30,1666 | 37,8568 |
| 27 | 1,3082 | 1,3985 | 1,4948 | 1,5975 | 1,7069 | 2,2213 | 2,8834 | 3,7335 | 4,8223 | 6,2139 | 7,9881 | 10,2451 | 13,1100 | 21,3249 | 34,3899 | 43,5353 |
| 28 | 1,3213 | 1,4160 | 1,5172 | 1,6254 | 1,7410 | 2,2879 | 2,9987 | 3,9201 | 5,1117 | 6,6488 | 8,6271 | 11,1671 | 14,4210 | 23,8839 | 39,2045 | 50,0656 |
| 29 | 1,3345 | 1,4337 | 1,5400 | 1,6539 | 1,7758 | 2,3566 | 3,1187 | 4,1161 | 5,4184 | 7,1143 | 9,3173 | 12.1722 | 15,8631 | 26,7499 | 44,6931 | 57,5755 |
| 30 | 1,3478 | 1,4516 | 1,5631 | 1,6828 | 1,8114 | 2,4273 | 3,2434 | 4,3219 | 5,7435 | 7,6123 | 10,0627 | 13,2677 | 17,4494 | 29,9599 | 50,9502 | 66,2118 |
ТАБЛИЦА С-4. Будущая стоимость аннуитета $1 за период 
| 1,00% | 1,25% | 1,50% | 1,75% | 2,00% | 3,00% | 4,00% | 5,00% | 6,00% | 7,00% | 8,00% | 9,00% | 10,00% | 12,00% | 14,00% | 15,00% | |
| 1 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 2 | 2,0100 | 2,0125 | 2,0150 | 2,0175 | 2,0200 | 2,0300 | 2,0400 | 2,0500 | 2,0600 | 2,0700 | 2,0800 | 2,0900 | 2,1000 | 2,1200 | 2,1400 | 2,1500 |
| 3 | 3,0301 | 3,0377 | 3,0452 | 3,0528 | 3,0604 | 3,0909 | 3,1216 | 3,1525 | 3,1836 | 3,2149 | 3,2464 | 3,2781 | 3,3100 | 3,3744 | 3,4396 | 3,4725 |
| 4 | 4,0604 | 4,0756 | 4,0909 | 4,1062 | 4,1216 | 4,1836 | 4,2465 | 4,3101 | 4,3746 | 4,4399 | 4,5061 | 4,5731 | 4,6410 | 4,7793 | 4.9211 | 4,9934 |
| 5 | 5,1010 | 5,1266 | 5,1523 | 5,1781 | 5,2040 | 5,3091 | 5,4163 | 5,5256 | 5,6371 | 5,7507 | 5,8666 | 5,9847 | 6,1051 | 6,3528 | 6,6101 | 6,7424 |
| 6 | 6,1520 | 6,1907 | 6,2296 | 6,2687 | 6,3081 | 6,4684 | 6,6330 | 6,8019 | 6,9753 | 7,1533 | 7,3359 | 7,5233 | 7,7156 | 8,1152 | 8,5355 | 8,7537 |
| 7 | 7,2135 | 7,2680 | 7,3230 | 7,3784 | 7,4343 | 7,6625 | 7,8983 | 8,1420 | 8,3938 | 8,6540 | 8,9228 | 9,2004 | 9,4872 | 10,0890 | 10,7305 | 11,0668 |
| 8 | 8,2857 | 8,3589 | 8,4328 | 8,5075 | 8,5830 | 8,8923 | 9,2142 | 9,5491 | 9,8975 | 10,2598 | 10,6366 | 11,0285 | 11,4359 | 12,2997 | 13,2328 | 13,7268 |
| 9 | 9,3685 | 9,4634 | 9,5593 | 9,6564 | 9,7546 | 10,1591 | 10,5828 | 11,0266 | 11,4913 | 11,9780 | 12,4876 | 13,0210 | 13,5795 | 14,7757 | 16,0853 | 16,7858 |
| 10 | 10,4622 | 10,5817 | 10,7027 | 10,8254 | 10,9497 | 11,4639 | 12,0061 | 12,5779 | 13,1808 | 13,8164 | 14,4866 | 15,1929 | 15,9374 | 17,5487 | 19,3373 | 20,3037 |
| 11 | 11,5668 | 11,7139 | 11,8633 | 12,0148 | 12,1687 | 12,8078 | 13.4864 | 14,2068 | 14.9716 | 15,7836 | 16,6455 | 17,5603 | 18,5312 | 20,6546 | 23,0445 | 24,3493 |
| 12 | 12,6825 | 12,8604 | 13,0412 | 13,2251 | 13,4121 | 14,1920 | 15,0258 | 15,9171 | 16,8699 | 17,8885 | 18,9771 | 20,1407 | 21,3843 | 24,1331 | 27,2707 | 29,0017 |
| 13 | 13,8093 | 14,0211 | 14,2368 | 14,4565 | 14,6803 | 15,6178 | 16,6268 | 17,7130 | 18,8821 | 20,1406 | 21,4953 | 22,9534 | 24,5227 | 28,0291 | 32,0887 | 34,3519 |
| 14 | 14,9474 | 15,1964 | 15,4504 | 15,7095 | 15,9739 | 17,0863 | 18,2919 | 19,5986 | 21,0151 | 22,5505 | 24,2149 | 26,0192 | 27,9750 | 32,3926 | 37,5811 | 40,5047 |
| 15 | 16,0969 | 16,3863 | 16,6821 | 16,9844 | 17,2934 | 18,5989 | 20,0236 | 21,5786 | 23,2760 | 25,1290 | 27,1521 | 29,3609 | 31,7725 | 37,2797 | 43,8424 | 47,5804 |
| 16 | 17,2579 | 17,5912 | 17,9324 | 18,2817 | 18,6393 | 20,1569 | 21,8245 | 23,6575 | 25,6725 | 27,8881 | 30,3243 | 33,0034 | 35,9497 | 42,7533 | 50,9804 | 55,7175 |
| 17 | 18,4304 | 18,8111 | 19,2014 | 19,6016 | 20,0121 | 21,7616 | 23,6975 | 25,8404 | 28,2129 | 30,8402 | 33,7502 | 36,9737 | 40,5447 | 48,8837 | 59,1176 | 65,0751 |
| 18 | 19,6147 | 20,0462 | 20,4894 | 20,9446 | 21,4123 | 23,4144 | 25,6454 | 28,1324 | 30,9057 | 33,9990 | 37,4502 | 41,3013 | 45,5992 | 55,7497 | 68,3941 | 75,8364 |
| 19 | 20,8109 | 21,2968 | 21,7967 | 22,3112 | 22,8406 | 25,1169 | 27,6712 | 30,5390 | 33,7600 | 37,3790 | 41,4463 | 46,0185 | 51,1591 | 63,4397 | 78,9692 | 88,2118 |
| 20 | 22,0190 | 22,5630 | 23,1237 | 23,7016 | 24,2974 | 26,8704 | 29,7781 | 33,0660 | 36,7856 | 40,9955 | 45,7620 | 51,1601 | 57,2750 | 72,0524 | 91,0249 | 102.4436 |
| 21 | 23,2392 | 23,8450 | 24,4705 | 25,1164 | 25,7833 | 28,6765 | 31,9692 | 35,7193 | 39,9927 | 44,8652 | 50,4229 | 56,7645 | 64,0025 | 81,6987 | 104,7684 | 118,8101 |
| 22 | 24,4716 | 25,1431 | 25,8376 | 26,5559 | 27,2990 | 30,5368 | 34,2480 | 38,5052 | 43,3923 | 49,0057 | 55,4568 | 62,8733 | 71,4027 | 92,5026 | 120,4360 | 137,6316 |
| 23 | 25,7163 | 26,4574 | 27,2251 | 28,0207 | 28,8450 | 32,4529 | 36,6179 | 41,4305 | 46,9958 | 53,4361 | 60,8933 | 69,5319 | 79,5430 | 104,6029 | 138,2970 | 159,2764 |
| 24 | 26,9735 | 27,7881 | 28,6335 | 29,5110 | 30,4219 | 34,4265 | 39,0826 | 44,5020 | 50,8156 | 58.1767 | 66,7648 | 76,7898 | 88,4973 | 118,1552 | 158,6586 | 184,1678 |
| 25 | 28,2432 | 29,1354 | 30,0630 | 31,0275 | 32,0303 | 36,4593 | 41,6459 | 47,7271 | 54,8645 | 63.2490 | 73,1059 | 84,7009 | 98,3471 | 133,3339 | 181,8708 | 212,7930 |
| 26 | 29,5256 | 30,4996 | 31,5140 | 32,5704 | 33,6709 | 38,5530 | 44,3117 | 51,1135 | 59,1564 | 68,6765 | 79,9544 | 93,3240 | 109,1818 | 150,3339 | 208,3327 | 245,7120 |
| 27 | 30,8209 | 31,8809 | 32,9867 | 34,1404 | 35,3443 | 40,7096 | 47,0842 | 54,6691 | 63,7058 | 74,4838 | 87,3508 | 102,7231 | 121,0999 | 169,3740 | 238,4993 | 283,5688 |
| 28 | 32,1291 | 33,2794 | 34,4815 | 35,7379 | 37,0512 | 42,9309 | 49,9676 | 58,4026 | 68,5281 | 80,6977 | 95,3388 | 112,9682 | 134,2099 | 190,6989 | 272,8892 | 327,1041 |
| 29 | 33,4504 | 34,6954 | 35,9987 | 37,3633 | 38,7922 | 45,2189 | 52,9663 | 62,3227 | 73,6398 | 87,3465 | 103,9659 | 124,1354 | 148,6309 | 214,5828 | 312,0937 | 377,1697 |
| 30 | 34,7849 | 36,1291 | 37,5387 | 39,0172 | 40,5681 | 47.5754 | 56,0849 | 66,4388 | 79,0582 | 94,4608 | 113,2832 | 136,3075 | 164,4940 | 241,3327 | 356,7868 | 434,7451 |
Сведения об авторах
Джитендранейтон Тадавилил (Jithendranathan Thadavillil) – профессор университета Сент-Томаса (St.Thomas), Миннесота, США
Кравченко Наталия Александровна – профессор ЭФ НГУ, д.э.н. Читает курсы «Финансовый менеджмент», «Инвестиционный менеджмент» для студентов отделения Менеджмент ЭФ НГУ, слушателей программ дополнительного профессионального образования. Ведущий научный сотрудник Института экономики и ОПП СО РАН.
Черемисина Татьяна Петровна, доцент ЭФ НГУ, к.э.н. Читает курс «Финансовый менеджмент» для студентов отделения Менеджмент, Экономики и управления ЭФ НГУ, слушателей программ дополнительного профессионального образования. Старший научный сотрудник Института экономики и ОПП СО РАН.
Юсупова Альмира Талгатовна, доцент ЭФ НГУ, д.э.н. Читает курсы «Финансовый менеджмент», «Отраслевые рынки» для студентов отделения Менеджмент, Экономики и управления ЭФ НГУ, слушателей программ дополнительного профессионального образования. Старший научный сотрудник Института экономики и ОПП СО РАН.
Финансовый менеджмент
Учебное пособие
Подписано в печать 02.09.13 Формат 60х84 1/8
Печать офсетная Уч.-изд. л. 14,75
Заказ №. Тираж 250 экз.
Редакционно-издательский центр НГУ
630090, Новосибирск-90, ул. Пирогова, 2
*
В отечественной литературе понятия приведения и дисконтирования денежных потоков иногда употребляются как синонимы, но это не вполне корректно.
[1]
http://vitis-ocenka.ucoz.ua/load/5-1-0-4.
[2]
Здесь предполагается, что уровень долга в структуре капитала остается постоянным в течение бесконечного времени, и процентные платежи по долгу фиксированы.
[3] Стоимость фирмы сейчас равна $7000, а долг составляет половину этой величины, то есть $3500.
1 www.Damodaran.com , Stern School of Business at New York University
*
http://www.bcs-express.ru/show_res_ru.asp?id=9320
*
Можно задавать требуемый компанией уровень чистого дохода от проекта NPV.
Дата: 2019-02-02, просмотров: 262.
