В данной главе на основе концепции временной стоимости денег (глава 1) мы оценим стоимость финансовых активов двух видов, а именно облигаций и акций. На практике можно применять некоторые из рассмотренных ниже методов оценки и к другим активам, в том числе нефинансовым.

Общая формула оценки

Активы с точки зрения экономики это то, что создает будущие доходы. Стоимость активов в конкретный момент времени зависит от будущих доходов, которые они принесут. Поскольку мы уже знаем, как оценивать текущую стоимость будущих доходов, мы можем записать общую формулу оценки в следующем виде:

PV=Present 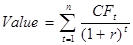                                                     (3.1)

В этом уравнении стоимость активов сегодня (настоящая стоимость - PV) представляет собой сумму дисконтированных стоимостей всех будущих доходов, которые принесет данный актив.

CF_t — это будущий доход в период t, а r — дисконтная ставка.

Эта модель может быть применена к любым активам, которые в будущем могут принести доходы.

Рассмотрим теперь модели оценки стоимости облигаций и акций.

Оценка облигаций

Облигации — это финансовые долговые инструменты, выпускаемые правительствами, правительственными учреждениями или частными корпорациями. Существует много типов облигаций. По купонным облигациям делаются периодические выплаты - так называемые купонные платежи, а также окончательная выплата основной суммы займа - так называемого номинала. Ниже приведена последовательность доходов и расходов по типичной купонной облигации.

        0             1            2                  3

Цена покупки Купон               Купон         Купон

(расход)                                                     + Номинал

Цена — это стоимость облигации. Купонные выплаты выражаются в процентах от номинала. Например, если номинал облигации составляет 1000 руб., а выплата по купонам 10 %, то ежегодные выплаты составят 1000 ´ 0,10 = 100 руб.

Рассмотрим оценку облигации на следующем примере.

Пример 1: Допустим, 1 января 2011 года фирма выпустила облигации с купоном 10% и сроком погашения три года. Выплаты по купонам осуществляются один раз в год. Номинал облигации составляет 1000 руб. Сколько должна стоить эта облигация 1 января 2011 года, если требуемая инвестором доходность равна 10%?

Time-line облигации можно представить следующим образом:

1 янв. 11            1 янв. 12                                     1 янв. 13         1 янв. 14

Цена?                       100                                           100                  100

                                                                                                                               1000

По этой облигации предусмотрены равные фиксированные платежи в течение фиксированного срока, а ее стоимость на 1 января 2011 года равна сумме дисконтированных всех будущих платежей.

Доходность, которую ожидает (требует) инвестор, является той дисконтной ставкой, которая используется для оценки облигации. В отношении облигаций дисконтная ставка носит особое название — доходность к погашению ( Yield To Maturity – YTM ) и обозначается буквой у (а не r ).

Для определения текущей цены равнокупонной облигации необходимо дисконтировать все доходы по ней. Поэтому используется комбинация двух формул - для оценки PV аннуитета и PV однократного вложения:

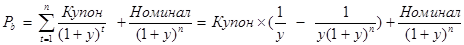   (3.2)

Подставив известные величины в это уравнение, получим цену облигации:

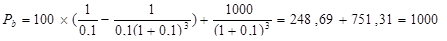руб.

Итак, цена облигации на 1 января 2011 г. равна 1000 руб, т.е. совпадает с ее номиналом. Такие облигации называются паритетными. Заметим также, что для паритетных облигаций ставка выплат по купонам совпадает со ставкой дисконтирования – доходностью к погашению.