Ожидаемая доходность инвестиционного портфеля определяется как средневзвешенное значение доходностей отдельных акций в портфеле. Она рассчитывается по следующей формуле:

                    (2.12)

Как и в случае расчета фактической доходности, веса представляют долю акций по стоимости в общем объеме портфеля.

Расчет риска для портфеля

Степень риска для портфеля определяется как стандартное отклонение ожидаемой доходности. Но в отличие от доходности портфеля риск для него не равен взвешенному среднему стандартных отклонений отдельных акций в портфеле. Прежде чем привести общую формулу для расчета этого риска, рассмотрим пример портфеля, состоящего из двух видов акций.

Пример 13: Используя данные примера 12, рассчитаем ожидаемую доходность и стандартное отклонение для портфеля, состоящего из акций А и В в соотношении 50:50.

Сначала вычислим ожидаемую доходность портфеля для разных состояний экономики.

Состояние экономики  Вероятность   E₀[r_Aj]E₀[r_Bj]E₀[r_pj]

Бурный рост                   0,20                25% 11 %              18,0 %

Умеренный рост            0,20                15% 20 %           17,5 %

Медленный рост                           0,40                10% 9 %              9,5 %

Спад                                 0,20                - 5% -15 %             -10,0 %

                                           1,00

Доходность портфеля для каждого состояния экономики рассчитывается путем вычисления взвешенного среднего доходностей отдельных акций для этого состояния. Например, доходность портфеля при бурном росте экономики равна E₀[r_pрост] = 0,5 х 25 +0,5 х 11 = 18 %. Вычислим ожидаемую доходность портфеля.

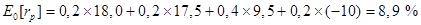
Изменчивость ожидаемой доходности равна

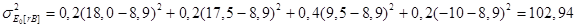
Стандартное отклонение для портфеля:

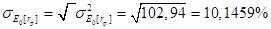
Взвешенное среднее двух стандартных отклонений равно: 0,5·9,6954+0,5·11,6344 = 10,6649 %.

В то же время стандартное отклонение для портфеля равно лишь 10,1459 %. Эта разница объясняется тем, что ожидаемые доходности входящих в портфель ценных бумаг не полностью коррелируют.

Какие же практические преимущества дает диверсификация?

Изменения в экономике по-разному влияют на разные акции. Если инвестор объединяет в портфеле акции разных компании, доходности которых при изменении состояний экономики меняются в разных направлениях, то эти изменения доходностей отдельных акций в портфеле несколько сглаживаются, что снижает риск инвестиций. Причем, снижение риска портфеля при этом не коррелирует со снижением доходности.

Приведенный выше метод оценки риска для портфеля довольно сложен, и становится почти неприменимым на практике, если портфель содержит много разных видов акций. Ниже приводится общая формула для оценки стандартного отклонения портфеля, состоящего из двух видов акций.

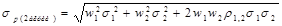         (2.13)

Здесь w₁ и w₂ — веса акций видов 1 и 2 в портфеле, s ₁ и s ₂ — стандартные отклонения ожидаемой доходности этих акций, а r _1,2 — коэффициент корреляции между доходностями акций.

По этой формуле можно вычислить стандартное отклонение портфеля в примере 13.

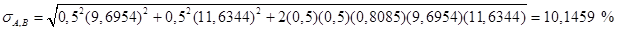
Оценка стандартного отклонения ожидаемой доходности получается такой же.

Общая формула для вычисления стандартного отклонения ожидаемой доходности портфеля, состоящего из n акций, записывается следующим образом:

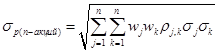                        (2.14)

Если в портфеле много акций, такие вычисления трудно провести вручную. Существуют компьютерные программы, позволяющие сделать это легко и быстро.