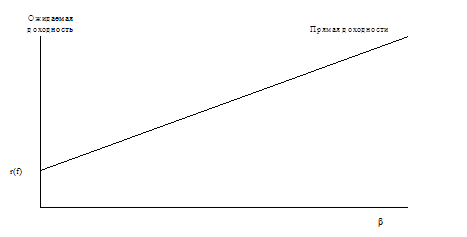
Уравнение 2.18 - это уравнение прямой линии, определяемой доходностью активов с нулевым риском и рыночной премией за риск. Таким образом, если построить график ожидаемой доходности в зависимости от бета-коэффициента, то получится прямая линия, называемая линией рынка ценных бумаг (Security market line, или SML).
|
Рис. 2.10 . Линия рынка ценных бумаг
Инвесторы меняют свою оценку ценных бумаг, если ожидаемая доходность отличается от доходности бумаг с близким уровнем риска. Общая формула для вычисления ожидаемой доходности представлена моделью САРМ. Объединяя их, получаем общую модель равновесных цен.
В наших рассуждениях использовалась предпосылка о том, что все инвесторы одинаково прогнозируют доходность активов с нулевым риском, среднерыночную доходность, а также доходность конкретных акций и их бета-коэффициенты. Поскольку они заботятся только об общерыночном риске (риск отдельных акций можно игнорировать благодаря диверсификации), они используют приведенную выше модель для оценки ожидаемой доходности акций. Зависимость между ожидаемой доходностью и бета-коэффициентом линейна, поэтому все комбинации доходность-бета должны лежать на прямой доходности. Если такая комбинация лежит в стороне, цены будут меняться, пока все такие комбинации не окажутся опять на прямой доходности. Рассмотрим пример.
Пример 17: Имеется следующая информация об акциях А и В:.
Акции P0 E0[P1] b j
A $50 $56,70 1,2
B $55 $60,00 1,2
Среднерыночная ожидаемая доходность 12%, доходность активов с нулевым риском 5%. Находятся ли цены на акции А и В в равновесии? Если нет, какими должны быть равновесные цены?
Прежде всего, рассчитаем ожидаемую доходность акций на основе модели САРМ.
E0[rA] = E0[rB] = 5 + (12-5)1,2 = 13,4%
Если предполагать, что рынок прогнозирует одинаковое изменение цен, то текущая цена должна быть равной сегодняшней ценности ожидаемой будущей цены. Зная прогнозируемые цены и ожидаемую готовность, мы можем рассчитать сегодняшние цены следующим образом:
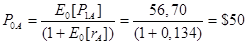
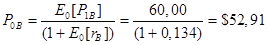
Сравнивая сегодняшние цены, можно увидеть, что цена на акции А находится в соответствии с САРМ, а цена на В слишком высока. Умные инвесторы начнут продавать акции В без покрытия, что увеличит их предложение на рынке и снизит цену на них, пока она не достигнет уровня $52,91.
Коэффициент b для портфеля
Значение b для портфеля определяется как средневзвешенное значение коэффициентов для отдельных акций в портфеле, в соответствии со следующей формулой:
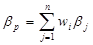(2.19)
Очевидно, что эта формула похожа на формулу доходности портфеля.
Пример 18: Предположим, что вы имеете в портфеле следующие акции.
Акция Сумма, руб. bj
A 5000 0,9
B 8000 1,1
C 7000 1,2
20000
Доходность акций с нулевым риском составляет 4 %, а ожидаемая среднерыночная доходность — 10 %. Какова ожидаемая доходность портфеля? Если для снижения уровня риска портфеля вы продадите В и С и замените их акциями D с b = 1, какой будет ожидаемая доходность нового портфеля?
Для текущего состава портфеля b вычисляется следующим образом:
bp = 0,25´0,9 + 0,4´1,1 + 0,35´1,2 = 1,085
Ожидаемая доходность портфеля: E0[rp] = 4 + (10-4)1,085 = 10,51%
При замене акций B и C изменятся веса акций в портфеле:
Вес
A 5000/20000 = 0,25
D 15000/20000 =0,75
Значение b для нового портфеля: bp(New) = 0,25´0,9 + 0,75´1,0 = 0,975
Ожидаемая доходность нового портфеля: E0[rp(New)] = 4 + (10-4)0,975 = 9,85 %
Оценка b
Как было показано, значение b равно отношению ковариации ожидаемой доходности акций со среднерыночной доходностью и вариации ожидаемой среднерыночной доходности. На практике оценить вариации и ковариации ожиданий довольно трудно. Поэтому для оценки b вместо ожидаемой можно использовать фактическую доходность. При этом предполагается, что соотношение между доходностью конкретных акций и среднерыночной доходностью со временем не изменяется, и поэтому ковариацию фактической доходности можно использовать в качестве оценки ковариации будущей доходности. Тот же аргумент применим и к вариации доходности, поскольку она тоже стабильна во времени.
Обычно для вычисления b используются фактические данные о доходности акций за последние шестьдесят месяцев. Можно применить следующую формулу регрессии.
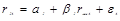(2.20)
Здесь rjt и rmt — фактическая доходность акций j и среднерыночная доходность за месяц t. Коэффициент регрессии b j дает оценку b для акций j, и aj — свободный член регрессии. Последний член e t представляет ошибку.
Рассмотрим оценку b на примере.
Пример 19: Ниже приведены данные по доходности за двенадцать месяцев. Рассчитать значение b для этих акций.
| Месяц | Среднерыночная доходность | Доходность акций |
| Январь-00 | -0,02477 | -0,21987 |
| Февраль-00 | 0,008386 | -0,19976 |
| Март-00 | 0,043504 | 0,086306 |
| Апрель-00 | 0,032357 | -0,24323 |
| Май-00 | 0,008062 | 0,31809 |
| Июнь-00 | -0,00201 | 0,431889 |
| Июль-00 | 0,045315 | -0,00034 |
| Август-00 | -0,02442 | -0,13343 |
| Сентябрь-00 | 0,026419 | -0,04922 |
| Октябрь-00 | -0,01848 | -0,15595 |
| Ноябрь-00 | 0,02792 | -0,04122 |
| Декабрь-00 | 0,028207 | 0,115192 |
Уравнение регрессии 3.19 дает следующие значения для линейной зависимости:
aj = -0,02435 bj = 1,33312
На рис.3.10 показан график регрессии. Линия регрессии называется характеристической прямой.
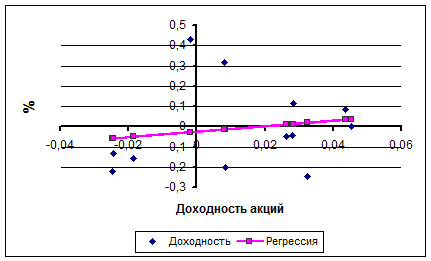
Рис. 3.10. Характеристическая прямая
Прямая с коэффициентом наклона 1,33312 и есть прямая регрессии. Сравнение данных среднерыночной доходности и доходности акций j показывает, что имеется значительный разброс значений. Этот момент следует учитывать при использовании метод регрессии для оценки b в реальных ситуациях. Для определения статистической значимости оценки b нужно использовать другие статистические показатели, например, R2.
Выводы
Компромисс между риском и доходностью является одним из ключевых понятий в финансах. В данное главе было рассмотрено различие между фактической (ex-post) и ожидаемой (ex-ante) доходностью. Рискованность вложения средств определяется вариацией его ожидаемой доходности. Для измерения риска используется стандартное отклонение.
Объединение акций в портфели уменьшает общий риск. Причина этого — в отсутствии полной корреляции между доходностями отдельных акций. Можно использовать понятия риска и доходности для нахождения множества эффективных портфелей.
Вкладчики ориентируются на собственные критерии для того, чтобы выбрать из множества эффективных портфелей оптимальный вариант. Если на рынке существуют ценные бумаги с нулевым риском, то можно выбирать из различных комбинаций таких бумаг и бумаг с неопределенной доходностью.
Риск, связанный с вложением средств в акции можно разделить на системный риск и риск отдельной фирмы. Диверсификация позволяет игнорировать риск, связанный с конкретными акциями, но остается систематический риск, связанный с состоянием всего рынка. Уровень системного риска для разных акций может быть разным, для его характеристики используется параметр b.
Было показано, что при определенных ограничениях можно найти равновесное соотношение между ожидаемой доходностью конкретных акций, ожидаемой доходностью рынка, и доходностью с нулевым риском. Это соотношение называется моделью САРМ.
Контрольные вопросы по теме «Доходность и риск»
1. Почему в финансах различается доходность ex-post и ex-ante? В чем суть этого различия? Каковы возможные подходы к оценке доходности ex-ante?
2. Какие инвестиционные предположения стоят за выбором принципа усреднения, лежащего в основе исчисления среднего дохода от инвестиций за период свыше года?
3. В чем суть маржинальной покупки на рынке ценных бумаг и при каком условии она может реализоваться? В чем ее выгода? Кто является ее участниками?
4. В чем суть короткой продажи на рынке ценных бумаг и при каком условии она может реализоваться? В чем ее выгода? Кто является ее участниками?
5. С помощью каких критериев оценивается движение случайных величин, какое применение это нашло в теории портфеля?
6. Как в финансах определяются доходность и риск актива? Опишите алгоритм расчета риска.
7. Опишите алгоритм расчета ожидаемой доходности и риска портфеля.
8. Почему возможна диверсификация портфеля и в чем ее смысл?
9. Дайте 4 интерпретации коэффициента бета (β).
10. Какие виды риска необходимо учитывать при оценке портфеля? Что является мерой риска каждого вида? Приведите примеры рисков каждого вида.
11. Какие прогнозы позволяет делать модель CAPM?
12. Определите понятие "линия рынка ценных бумаг", дайте геометрическую интерпретацию и связь с моделью равновесных цен.
13. Почему различаются систематический (рыночный) и несистематический (индивидуальный) риски? Приведите примеры различных типов рисков, связанных с вложением в российские ценные бумаги.
Справочные материалы по теме[1] на 26.08.2009
Дата: 2019-02-02, просмотров: 379.
