Как отмечалось выше, ключевым фактором, определяющим полезность диверсификации, является корреляция ожидаемой доходности отдельных акций. Рассмотрим влияние изменения коэффициента корреляции на формирование множества портфелей. Прежде всего, рассмотрим те же акции, что и в примере 14, но с коэффициентом корреляции –1. Вычислим стандартные отклонения для этого случая.
 |
Начиная с портфеля 1, стандартное отклонение убывает и равно 0% для портфеля 4.
Уровень риска для портфеля 4 равен 0, т.е. это безрисковый портфель. При объединении в портфеле из двух бумаг акций с коэффициентом корреляции -1 существует портфель с нулевым риском. Ниже на графике показан набор эффективных портфелей.
Приведенный график состоит из двух прямолинейных сегментов. В первом (нижнем) сегменте находятся неэффективные портфели (их доходность невысока), а во втором — эффективные (их доходность при уровне риска от 8,14 до 0% выше, чем в первом сегменте).
При уровне риска, скажем, в 5% инвестор имеет возможность выбирать из двух вариантов портфеля – в нижнем сегменте доходность составит около 12%, в верхнем – почти 20%. Очевидно, что предпочтение будет отдано портфелю с более высокой доходностью.
Очевидно так же и то, что пространство выбора ограничено областью риска от 8,14 до 5%. Если инвестор определил для себя приемлемым уровень риска, превышающий 8,14%, например, в 10%, то выбора уже не будет, потому что этому условию отвечает один единственный портфель с доходностью около 24%.
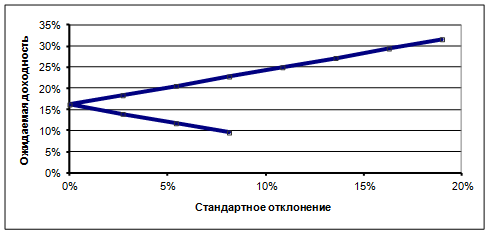
Рис. 2.5. Множество эффективных портфелей —
пример портфеля из двух акций с корреляцией -1
Рассмотрим теперь другой крайний случай, в котором коэффициент корреляции доходностей равен +1. Ниже показаны ожидаемые доходности и стандартные отклонения для данных портфелей.
| Вес А | Вес В | Стандартное отклонение | Доходность портфеля | |
| Портфель 1 | 1,0 | 00,0 | 8,14 % | 9,50 % |
| Портфель 2 | 0,9 | 0,1 | 9,23 % | 11,71 % |
| Портфель 3 | 0,8 | 0,2 | 10,31 % | 13,92 % |
| Портфель 4 | 0,7 | 0,3 | 11,40 % | 16,13 % |
| Портфель 5 | 0,6 | 0,4 | 12,48 % | 18,34 % |
| Портфель 6 | 0,5 | 0,5 | 13,57 % | 20,55 % |
| Портфель 7 | 0,4 | 0,6 | 14,66 % | 22,76 % |
| Портфель 8 | 0,3 | 0,7 | 15,74 % | 24,97 % |
| Портфель 9 | 0,2 | 0,8 | 16,83 % | 27,18 % |
| Портфель 10 | 0,1 | 0,9 | 17,91 % | 29,39 % |
| Портфель 11 | 0,0 | 1,0 | 19,00 % | 31,60 % |
В этом случае ожидаемые доходности и стандартные отклонения увеличиваются. Ниже показан график ожидаемой доходности и стандартного отклонения.
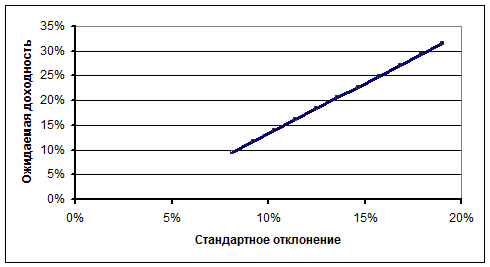
Рис. 2.6. Множество эффективных портфелей —
пример портфеля из двух акций с корреляцией +1
В этом множестве совсем нет неэффективных портфелей. Поскольку допустимый набор — прямая линия, она характеризуется постоянным углом наклона. Следовательно, уровень риска возрастает прямо пропорционально росту ожидаемой доходности. Соединение таких акций в портфель не дает преимуществ диверсификации.
В реальных ситуациях коэффициент корреляции ожидаемой доходности лежит между двумя крайними значения. Как правило, ожидаемые доходности имеют положительную корреляцию, хотя она и меньше +1. При соединении в портфеле акции с неполной корреляцией, диверсификация оказывается полезной.
Мы показали, как связаны уровень риска и доходность, а также как найти эффективные портфели. Следующий вопрос — как выбрать из набора эффективных портфелей тот, который удовлетворяет критериям инвестора.
Дата: 2019-02-02, просмотров: 410.