В тех случаях, когда средства инвестируются на длительный срок, требуется рассчитывать общую и среднегодовую доходности вложения. Рассмотрим два разных способа усреднения: среднее арифметическое и среднее геометрическое.
Расчет среднегодовой доходности по среднеарифметическому значению. Доходность рассчитывается за каждый период и по следующей формуле берется среднее арифметическое:
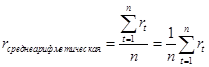, (2.2)
где rt – доходность за год t, а n – число лет.
Отметим, что этот способ используется редко. Здесь предполагается, что сумма инвестиции не меняется, т.е. прибыль, получаемая в конце каждого периода, изымается.
Пример 2: Допустим, что 1 января 2012 г. вы вложили 100 руб. в акции. К 31 декабря 2012 г. цена вложений поднялась до 200 руб., а к 31 декабря 2013 г. опустилась до 100 руб. Дивиденды по акциям не выплачивались. Найти доходность за 2012 и 2013 годы, а также среднюю доходность за два года.
1 января 2012 г. 31 декабря 2012 г. 31 декабря 2013 г.
P0=100 P1=200 P2=100
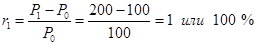
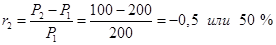
Среднеарифметическая доходность за два года равна rср.ар.= (100 % - 50 %)/2 = 25 %
Среднегодовая доходность по методу среднего геометрического: При использовании этого метода применяется следующая формула:
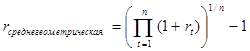(2.3)
Здесь предполагается реинвестирование получаемой в течение периода прибыли.
Пример 3: Найти среднегодовую доходность акции из примера 2 по методу среднего геометрического.
Подставим уже вычисленные значения годовой доходности в формулу 2.3.
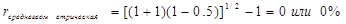
Значения, рассчитанные по этим методам, различаются. Как определить, какое из них правильное? На самом деле оба значения верны. Дело в том, что эти методы основаны на разных концепциях поведения инвестирования.
Как уже отмечалось, метод среднего арифметического предполагает, что в течение всего периода размер вклада не меняется. В приведенном выше примере это означает, что в конце первого года превышение курсовой разницы изымается инвестором в личный доход и остается только первоначально вложенная сумма, т.е. 1000 руб. Если акционер в нулевой момент приобрел 10 акций по 100 руб., израсходовав 1000 руб., то к концу года пакет его акций стал стоить 2000 руб. Поскольку усреднение доходности по методу среднего арифметического предполагает, что размер инвестиции не изменяется, это означает, что инвестор в конце первого года продает половину пакета (5 из 10) своих акций и полученные деньги направляет в личный доход, а пакет из оставшихся 5 акций опять стоит 1000 руб. В следующем периоде цена акций упала в 2 раза (на 50 %), поэтому теперь инвестор вынужден из личного дохода инвестировать 500 руб. для покупки 5 акций по 100 руб., чтобы размер вклада остался прежним (1000 руб.). Суммарный доход за два года определяется как (100 – 50 руб.), или в среднем 25 руб. в год. Таким образом, средний доход за период равен 25 % от суммы инвестиции Р0.
Но такое поведение инвестора не признается рациональным: они действительно так не поступают. Как правило, рациональный инвестор, цель которого состоит в увеличении стоимости своего пакета акций, реинвестируют получаемую прибыль. Поэтому и для расчета средней доходности более правильно использовать метод среднего геометрического, который, как отмечалось, основан на предположении о том, что все промежуточные доходы от вклада реинвестируются.
Пример 4: Предположим, что 1 июля 2010 г. вы приобрели 100 акций Корпорации XYZ по 50 руб. за акцию. Эта компания каждый год в конце июня выплачивает дивиденды в размере 1 руб. на акцию. Если на 30 июня 2011 г. цена акций составляла 50 руб., а на 30 июня 2012 г. - 60 руб., какой была среднегодовая доходность за двухлетний период?
2010 2011 2012
P0=50 P1=50 P2=60
D1=1 D2=1
Сначала подсчитаем доходность за каждый год, а потом вычислим среднегодовую доходность по методу геометрического среднего. Рассчитаем доходность (в расчете на 1 акцию) за год:
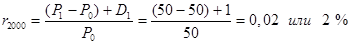
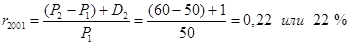
Среднегодовая доходность за двухлетний период по методу среднегеометрической средней рассчитывается следующим образом:
R2010-2012 = ((1+0,02)*(1+0,22)1/2 – 1 = 0,115527 или 11,5527%
Здесь предполагается, что 100 руб. дивидендов, полученных 30 июня 2011 г., были реинвестированы, т.е. на них куплены еще две акции по 50 руб. В конце второго года пакет инвестора увеличился на 2 акции: 100 + 2 = 102 акции.
Можно рассчитать доходность и иным путем - используя концепцию временной стоимости денег. Денежные потоки (в расчете на весь объем инвестиции), связанные с этой инвестицией, выглядят следующим образом:
1 июля 2010 г. 30 июня 2011 г. 30 июня 2012 г.
Инвестиция = -5000 руб. Дивиденды = 100 руб. Продажа акций = 6120 руб.
Покупка новых=-100 руб. Дивиденды = 102 руб.
акций (две акции) 6222 руб.
В нулевой момент на сумму в 5000 руб. приобретено 100 акций по цене 50 руб. (минус показывает, что это отток денежных средств). 30 июня 2011 г. получены дивиденды — 1 руб. на каждую акцию: 100*1=100 руб.
Полученный дивидендный доход был реинвестирован – куплены две дополнительные акции по 50 руб.
Наконец, 30 июня 2012 г. получены дивиденды в размере 1 руб. на каждую из 102 акций, а весь пакет акций вырос в цене до 6120 руб., поскольку каждая акция теперь стоит 60 руб.
Итого совокупный размер инвестиции уже составляет 6120+102 = 6222 руб.
Теперь можно рассчитать процентную ставку, при которой $5000 через два года превратятся в $6222.
Согласно формуле будущей стоимости (FV) вклада, приведенной в главе 2, нужно решить следующее уравнение:
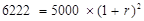, откуда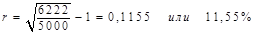 
Ставка процента равна 11,55 %, что совпадает со значением доходности, полученным выше.
Дата: 2019-02-02, просмотров: 267.
