Инфляцией называется повышение цен, и соответственно, снижение покупательной способности денег. Например, если сегодня плитка шоколада стоит 100 руб., а через год 2 руб., это означает, что через год на 100 руб. мы сможем купить лишь половину плитки, т.е. инфляция уменьшит стоимость денег наполовину.
При анализе изменения стоимости денег во времени следует учитывать влияние инфляции и упущенной прибыли (альтернативных издержек). Истинная стоимость денег в экономике называется реальной процентной ставкой, а наблюдаемая — номинальной процентной ставкой (r). Соотношение, связывающее номинальную процентную ставку, инфляцию и реальную процентную ставку, было выведено известным экономистом Ирвингом Фишером:
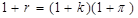(1.11)
или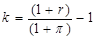 
где k — реальная процентная ставка, а p — показатель инфляции.
Это уравнение можно переписать и упростить следующим образом: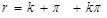 
Если реальная процентная ставка и темпы инфляции не слишком высоки, приближенно можно записать то же уравнение следующим образом:
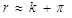(1.12)
Иначе говоря, номинальная процентная ставка приблизительно равна сумме реальной процентной ставки и инфляции при условии невысокой инфляции.
Пример 19: Допустим, вы инвестируете сегодня 1000 д.е. на 5 лет под номинальную процентную ставку 10%. Если уровень инфляции в течение этих пяти лет составит 4 %, какой будет настоящая стоимость вашего вклада через 5 лет?
Есть два разных способа решения этой задачи. Один способ — найти реальную процентную ставку и с ее помощью найти будущую стоимость. Реальная процентная ставка находится так: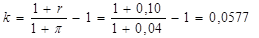 
Теперь используем это значение и уравнение 1.1 для того, чтобы найти будущую стоимость. Получаем ответ — 1323,72 д.е.
Другой способ состоит в определении будущей стоимости через номинальную ставку процента. Поскольку каждый год стоимость денег снижается из-за инфляции, с учетом показателя инфляции можно привести номинальную будущую стоимость к реальной будущей стоимости. Из уравнения 1.1 при номинальной процентной ставке вычисляется будущая стоимость, равная 1610,51 д.е. Теперь, чтобы найти реальную стоимость инвестиции в сегодняшних долларах, нужно дисконтировать будущую стоимость по ставке 4 %. Уравнение 2.5 показывает, что сегодняшняя стоимость этих 1610,51 д.е. равна 1323,72, т.е. ответ совпадает.
Контрольные вопросы по теме «Временная стоимость денег»
1. При каких условиях эффективная годовая ставка процента оказывается выше, а при каких - ниже номинальной ставки? Приведите примеры финансовых инструментов, по которым EAR выше или ниже номинальной ставки.
2. В будущем вас ожидает наследство. От каких факторов зависит настоящая стоимость вашего наследства? Дайте пояснение по каждому фактору.
3. Какой аннуитет дороже при прочих равных условиях – с выплатами в конце или в начале периода? Обоснуйте свой ответ на примере.
4. Можно ли пользоваться стандартными таблицами для вычисления настоящей и будущей стоимости аннуитета с выплатами в начале периода? Если можно, объясните, как и почему.
5. Что представляет собой ссуда в рассрочку? Какие факторы, заложенные в разные схемы погашения ссуды, «работают» на снижение риска банка?
6. Как взаимосвязаны между собой номинальная и реальная процентные ставки и инфляция?
7. От каких факторов зависит стоимость краткосрочных банковских кредитов?
8. Покажите на расчетном примере, влияет ли размер первоначального взноса на стоимость потребительского кредита, возвращаемого на условиях ссуды в рассрочку?
Глава 2. Риск и доходность
В данной главе мы рассмотрим два важнейших аспекта любого инвестиционного решения – риск и доходность. Концепция доходности относительно проста и легко воспринимаема, значительно труднее понять, что такое риск и особенно сложно оценить его. Цель данной главы — рассмотреть природу связи между риском и доходностью, показать, как она влияет на решения инвестора. Понятия риска и доходности используются применительно ко всем видам активов, мы будем анализировать в основном инструменты фондового рынка, т.е. инвестиции в ценные бумаги.
Измерение доходности
Доходность любого вложения капитала определяется будущими денежными поступлениями от этого вложения, которые формируются за счет повышения цены и периодических платежей. Например, если деньги вкладываются в акции, то для расчета доходности такого вложения нужно оценить изменение их цены и выплаченную сумму дивидендов за определенный период. При этом необходимо различать два способа расчета доходности: ex-post (после) и ex-ante (до) совершения события, т.е. до момента оценки доходности.
Расчет доходности (Ex-Post)
Доходность ex-post – это доходность вложения за период, рассчитанная по фактическим данным по его завершении. Рассмотрим простую модель расчета доходности для одного периода.
0 1
Цена в начале = P0 Цена в конце = P1
Дивиденд = D1
В приведенном примере рассматривается инвестиция в акцию, которая в конце периода стоит P1, кроме этого в конце периода на акцию выплачиваются дивиденды в размере D1. Если в конце периода инвестор продаст акцию, то он получит доход (P1 - P0), образующийся за счет изменения цены. Суммарный доход от вложения состоит из этой разницы и выплаченных дивидендов D1. Формула расчета общей фактической доходности (ex-post) за один период:
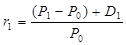(2.1)
где r1 — доходность вложения ex-post.
Заметим, что эта формула работает как для одной акции, так и для пакета, поскольку доходность – относительная величина, измеряемая в процентах за период.
Пример 1: Предположим, что 1 сентября 2012 г. вы купили акцию за 50 руб. Через год, 31 августа 2013 г., выплачиваются дивиденды в размере 1 руб., а цена акции равна 55 руб. Какова доходность ex-post для такого вложения капитала?
Подставив заданные значения в уравнение 2.1, получим:
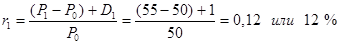
Далее термин «доходность» будет подразумевать фактическую доходность ex-post.
Дата: 2019-02-02, просмотров: 337.
