Часто по условиям ссуды заемщик должен выплачивать ее равными долями в течение определенного времени. Очевидно, что такие денежные выплаты составят аннуитет. Но каждый платеж будет состоять из двух частей: процента за кредит и часть основного долга. Следующий пример поможет нам понять, как это происходит.
Пример 15: 1 января 2013 года вы получили в банке ссуду в 10000 д.е. на три года. Вы планируете погасить этот долг за три равные платежа. Если процент по ссуде составляет 10 % с ежегодным начислением, сколько вы должны будете платить каждый год?
Для решения подобных задач необходимо использовать технику Time-Line:



 0 r =10 % 1 r 2 r 3
0 r =10 % 1 r 2 r 3

10000 С С С
Известны следующие данные: PV = 10000; t = 3; и r = 10 %.
Подставим эти значения в формулу для настоящей стоимости обычного аннуитета (уравнение 1.8) и рассчитаем платеж С:
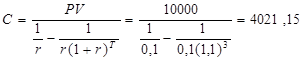
Каждый год вам нужно будет вносить 4021,15 д.е. Какая часть каждого платежа пойдет на покрытие процентов, а какая – на погашение основной суммы долга? Эти части можно определить следующим образом:
График амортизации (погашения) долга
| Год | Сумма долга на начало года | Процент 10 % | Основной платеж | Общая сумма платежа | Сумма долга на конец года |
| 1 | 10000 | 1000 | 3021,15 | 4021,15 | 6978,85 |
| 2 | 6978,85 | 697,89 | 3323,26 | 4021,15 | 3655,59 |
| 3 | 3655,59 | 365,56 | 3655,59 | 4021,15 | 0,00 |
Заметим, что в первых платежах большая их часть приходится на проценты, но со временем доля процентом уменьшается и растет доля, отчисляемая на погашение основной суммы долга. К концу периода основная сумма долга сокращается до нуля. Преимущество такого графика заключается в том, что вы можете определить точную сумму задолженности в конце каждого периода. Например, если вы хотите полностью погасить долг после двух лет, вам нужно выплатить 3655,59 д.е.
Но если частота, а значит и число платежей увеличится, например, заемщик должен вносить равные ежемесячные (m=12) платежи, то число строк в таблице, отражающей амортизацию долга, возрастет до 36, а месячный платеж сократится, но не в 12 раз:
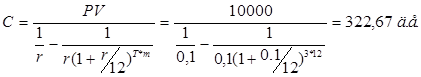
Мы видим, что, выплатив 36 раз по 322,67 д.е., заемщик в совокупности уплатит меньше, чем при погашении тремя ежегодными суммами: 36 * 322,67 = 11616,12 3 * 4021,15 = 12063,45
Очевидно, что рассмотренная процедура погашения ссуды уравновешивает риски заемщика и кредитора.
Процедуры погашения ссуды
Банки могут предложить заемщику ссуду с погашением в рассрочку на разных условиях. В зависимости от условий предоставления ссуды различают три процедуры (метода) погашения долга:
· Метод Инвуда: погашение долга равными суммами (одновременная выплата процентов и погашение основного долга);
· Метод Ринга погашение основного долга равными частями и выплата процентов по текущему долгу;
· Метод Хоскольда: регулярная выплата процентов по основному долгу и возврат ссуды в конце срока из погасительного фонда.
Рассмотрим все три метода на одном примере:
Пример 16: Размер ссуды 10000 д.е., срок – 4 года, ставка -14%, выплата 1 раз в конце года.
Метод Инвуда
Размер равного ежегодного платежа (С) в счет погашения ссуды рассчитывается как частное от деления суммы займа на соответствующий фактор аннуитета (PV аннуитета, в котором число периодов равно 4, ставка процента – 14% в месяц, таблица С-2): С = 10000/2,9137= 3432,06 д.е.
График погашения (амортизации) ссуды
| t | Сумма долга на начало года | Уплата про-центов (1%) | Размер платежа (С) | Погашение основной суммы долга | Сумма долга на конец года |
| 1 | 10000 | 1400 | 3432,06 | 2032,06 | 7967,94 |
| 2 | 7967,94 | 1115,51 | 3432,06 | 2316,55 | 5651,39 |
| 3 | 5651,39 | 791,20 | 3432,06 | 2640,87 | 3010,53 |
| 4 | 3010,53 | 421,47 | 3432,06 | 3010,53 | 0 |
| Итого: | 3728,18 | - |
Метод Ринга
Платеж по основному долгу: С = 10000/4 = 2500 д.е.
График погашения (амортизации) ссуды
| t | Сумма долга на начало года | Уплата про-центов (14%) | Размер платежа (С) | Погашение основной суммы долга | Сумма долга на конец года |
| 1 | 10000 | 1400 | 2500 | 3900 | 7500 |
| 2 | 7500 | 1050 | 2500 | 3550 | 5000 |
| 3 | 5000 | 700 | 2500 | 3200 | 2500 |
| 4 | 2500 | 350 | 2500 | 2850 | 0 |
| Итого: | 3500 | 10000 | 13500 | - |
Метод Хоскольда
Чтобы выплатить необходимую сумму к концу срока, заемщик предварительно ее накапливает. На накапливаемую сумму начисляется 10% ежегодно.
Вариант 1.
Равные ежегодные взносы формируют погасительный фонд, из которого ежегодно выплачиваются проценты по ссуде, а в конце срока погашается займ.
Размер ежегодного взноса С в погасительный фонд:
С = 10000 х (0,14 + 1/FV-фактор аннуитета-4 периода; 10%, табл. С-4) = 3554,71 д.е.
График погашения (амортизации) ссуды
| t | Сумма долга на начало года | Уплата про-центов (14%) | Взносы в погаси- тельный фонд (С) | Чистое накопление в год | Накопление нарастающим итогом |
| 1 | 10000 | 1400 | 3554,71 | 2154,71 | 2154,71 |
| 2 | 10000 | 1400 | 3554,71 | 2154,71 | 4524,89 |
| 3 | 10000 | 1400 | 3554,71 | 2154,71 | 7132,09 |
| 4 | 10000 | 1400 | 3554,71 | 2154,71 | 10000 |
| 5600 | 14218,84 | 8654,84 | - |
Вариант 2
Процент по ссуде ежегодно не выплачивается, а присоединяется к первоначальной сумме долга, следовательно, в конце срока кредита сумма к погашению увеличивается. Это увеличивает размер погасительного фонда, который следует накопить к концу срока, а значит, увеличивается и размер С равного ежегодного взноса в этот фонд.
С = 10000 х (1+0,14)4 х 1/FV-фактор аннуитета- 4 периода; 10%, табл. С-4) =
= 20000 х (1,144 х 1/4,6410) = 3639,30 д.е.
График погашения (амортизации) ссуды
| t | Сумма долга на начало года | Взносы в погасительный фонд (С) | Накопление нарастающим итогом | Сумма долга на конец года |
| 10000 | 3639,30 | 3639,30 | 11400 | |
| 11400 | 3639,30 | 7642,53 | 12996 | |
| 12996 | 3639,30 | 12046,08 | 14815,44 | |
| 14815,44 | 3639,30 | 16889,99 | 16889,60 | |
| Итого: | 14557,20 | - |
Дата: 2019-02-02, просмотров: 416.