Выплата процентов и возврат основной суммы долга осуществляется в этом случае равными частями в течение срока кредита (метод Инвуда), процент исчисляется на основе номинальной ставки и добавляется к основной сумме долга.

А. Т=1 год, погашение долга осуществляется ежемесячно, т.е. 12-тью равными платежами.

Расчет стоимости кредита на таких условиях делается в несколько этапов:

1) Расчет суммы по процентам: 10000*0,12 = 1200 д.е.

2) Расчет суммы, подлежащей возврату: 10000+1200 = 11200 д.е.

3) Расчет размера ежемесячного платежа в счет погашения ссуды: РМТ = 11200/12 = 933,33 д.е.

4) Построим time-line по оцениваемому инструменту:

0         1        2         3                                                                                      10     11  12

      -10000 933,33 933,33 933,33                                                                              933,33 933,33 933,33

При погашении заемщиком ссуды банк получает аннуитетные выплаты, настоящая стоимость PV которых равна 10000 д.е., т.е. сумме, полученной заемщиком на руки. Для определения стоимости кредита на таких условиях необходимо рассчитать месячную ставку доходности (для банка) по инструменту из уравнения:

10000 = 933,33 * PV-фактор аннуитета (12 периодов, r_мес.)

PV-фактор аннуитета (12 периодов, r_мес.) = 10000/933,33 = 10,71432

5) Расчет месячной доходности кредита для банка, которая равна его стоимости для заемщика.

Чтобы определить r_мес., обратимся к таблице С-2 и в строке 12 (12 периодов) найдем число, близкое 10,71432. Соответствующая этому числу ставка и будет приблизительной среднемесячной доходностью банка по выданной ссуде. Ее точное значение без труда рассчитывается в Excel – 1.788%.

6) Пересчитаем месячную ставку на годовую эффективную: ЕАR = (1 + 0,01788)¹² – 1 = 23,7%.

Это и есть реальная цена кредита на условиях дополнительного процента – она почти вдвое превышает номинальную ставку.

Б. Т=1/4 года, погашение долга осуществляется ежемесячно, т.е. тремя равными платежами.

Расчет стоимости кредита на таких условиях делается в несколько этапов:

1) Расчет суммы по процентам: 10000*(0,12/4) = 300 д.е.

2) Расчет суммы, подлежащей возврату: 10000+300 = 10300 д.е.

3) Расчет размера ежемесячного платежа в счет погашения ссуды: РМТ = 10300/3 = 3433,33 д.е.

4) Построим time-line по оцениваемому инструменту:

0         1          2              3

-10000 3433,33 3433,33    3433,33

Месячная ставка по аннуитету определяется из уравнения:

10000 = 3433,33 * PV-фактор аннуитета (3 периодов, r_мес.)

PV-фактор аннуитета (3 периодов, r_мес.) = 10000/3433,33 = 2,912621

5) Чтобы определить r_мес., обратимся к таблице С-2 и в строке 3 (3 периода) найдем число, близкое 2,912621. Соответствующая этому числу ставка и будет приблизительной среднемесячной доходностью банка по выданной ссуде – 1.5%.

6) Пересчитаем месячную ставку на годовую эффективную: ЕАR = (1 + 0,015)¹² – 1 = 19,56%.

Мы видим, что более короткие сроки кредита на таких условиях снижают его стоимость (срок кредита короче в 4 раза, а его стоимость ниже лишь на 17%).

4. Простой процент + компенсационный остаток

Иногда банки ужесточаю условия кредита требованием поддержания так называемого компенсационного остатка (СВ) на счету не ниже определенного уровня. Это значит, что заемщик не имеет права снимать со счета всю сумму и для него это оборачивается необходимостью увеличения номинальной суммы кредита, а следовательно, - удорожанием.

Итак, допустим, СВ составляет 20% от уровня займа.

А. Т=1 год

Номинальная сумма кредита рассчитывается по формуле:

Реальная сумма кредита/(1-СВ) = = 10000/(1-0,2) = 10000/0,8 = 12500 у.е.

Проценты начисляются на всю сумму кредита: 12500*0,12 = 1500 у.е.

EAR = 1500/10000 = 15% = 12%/(1-0.2) = 15%

Требование компенсационного остатка привело к повышению стоимости кредита с 12 до 15%.

Б. Т=1/4 года

Номинальная сумма кредита будет той же – 12500 у.е.

Проценты исчисляются на всю сумму кредита, но с учетом его срока: 12500/0,12/4 = 375 у.е.

Стоимость кредита за квартал = 375/10000 = 3,75%

ЕАR = (1 + 0,0375)⁴ – 1 = 15,87% - это несколько выше, чем в случае А.

5. Дисконтный процент + компенсационный остаток

А. Т = 1 год, СВ = 0,2

Номинальная сумма кредита = Требуемая сумма/(1-r_ном.-СВ) = 10000/(1-0,12-0,2) = 14705,88 у.е.

Проценты начисляются на всю сумму кредита: 14705,88 * 0,12 = 1764,71 у.е.

EAR= 1764,71/10000 = 17,65%

Б. Т = 1/4 года, СВ = 0,2

Номинальная сумма кредита = Требуемая сумма/(1-r_ном/4_.-СВ)=10000/(1-0,12/4-0,2) =10000/0,77=12987 у.е.

Проценты начисляются на всю сумму кредита: 12987* 0,12/4 = 389,6 у.е.

Стоимость кредита за квартал = 389,6/10000 = 3,896%

EAR= (1+0,03896)⁴ – 1 = 16,52% - это несколько ниже, чем в случае А.

Поток неравных платежей

Довольно часто при оценке финансовых проектов (планирование капитальных вложений) ставится задача оценки конечного потока неравных денежных платежей. Очевидно, что для ее решения необходимо определить PV или FV каждого платежа, а затем просуммировать их.

Тогда наши формулы будут выглядеть следующим образом:

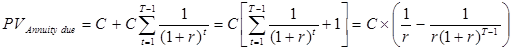
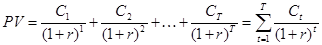
На следующем примере покажем, как в таком случае оценить будущую и текущую стоимость такого финансового инструмента как инвестиционный проект.

0                                 1                            2                       3

                                 600                                      500                      800                    

Здесь неприменима формула для аннуитета, поскольку в разные периоды платежи разные. Можно использовать либо специальный финансовый калькулятор, либо просуммировать отдельные дисконтированные платежи.

Пример 18: Найти будущую и настоящую стоимость проекта, если известно, что ожидаемые доходы составят 600 д.е. в конце первого года, 500 д.е. в конце второго и 800 д.е. в конце третьего года. Годовая процентная ставка равна 10 %.

Будущая стоимость проекта рассчитывается следующим образом:

0                        1                             2               3

              600                           500           800