Теоретически возможно уменьшать период начисления процентов до тех пор, пока он не станет бесконечно малым. В этом случае говорят о непрерывном начислении процентов и используют следующую формулу:

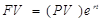                                                                                       (1.4)

Если в примере 3 мы применим формулу для непрерывного начисления процентов, то получим следующий результат:

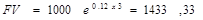
Очевидно, что разница между ежедневным и непрерывным начислением процентов очень мала. Фактически же банки не начисляют проценты чаще, чем ежедневно или ежемесячно.

Пример 5: Допустим, что банк начисляет проценты из расчета 12 % годовых. Тогда фактическая ставка при начислении процентов два раза в год составит

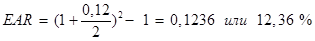
Это значит, что доход вкладчика составит 12,36 % в год. Например, если он вкладывает 1000 д.е. под 12 % годовых, то за три года при начислении раз в полгода его вклад вырастет до

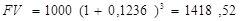д.е.

Именно это значение мы получили в примере 4. Понятие эффективной ставки помогает подсчитать реальный доход от вашего вклада, если проценты на него начисляются несколько раз в год.

Это справедливо и для случаев, когда начисление на вклад осуществляется реже, чем 1 раз в год. Но в этом случае эффективная ставка будет меньше, чем номинальная.

Пример 6: Допустим, вы заняли у товарища 1000 д.е. на 1,5 года, пообещав в конце срока вернуть 1233,24 д.е. Какой будет эффективная годовая ставка этого займа?

Номинальная ставка по займу за 1,5 года составит:

1233,24/1000 -1 = 23,324%

А теперь вернемся к формуле EAR :

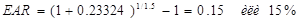
Таким образом, годовая эффективная ставка по этому займу составит 15%, а номинальная окажется выше.

Настоящая стоимость (Present Value – PV) однократного вложения

Настоящая (текущая) стоимость PV денег равна сегодняшней стоимости вложения, которое мы получим в будущем. Например, зная, какую сумму вы получите через год, можно сказать, какой сумме она эквивалентна сегодня. Это одно из самых важных понятий в финансах. Ранее мы рассмотрели будущую стоимость FV вклада, которая рассчитывается по формуле сложных процентов. Из того же уравнения можно вывести формулу расчета настоящей (текущей) стоимости вклада по известной будущей его стоимости:

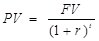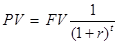                , или                          (1.5)

Задача в этом случае будет ставиться так: какую сумму денежных единиц PV вам сегодня следует инвестировать, чтобы через год (два, … t лет) в вашем распоряжении оказалось сумма, равная FV?

     0           1           2                                      t лет

  I            I           I                 ...                  I

PV=?      r           r                                 r FV

Способы нахождения PV те же, что FV: Таблица 1 (см. Приложение 1) дает оценку PV "неработающей", т.е. не приносящей доход, денежной единицы через заданный промежуток времени (от года до 55 лет) при фиксированном значении среднегодовой ставки процента. Заметим, что при оценке будущей стоимости финансисты используют для r название процентная ставка, а процесс определения FV называют приведением или наращением. При определении настоящей (текущей) стоимости они употребляют для r другой термин - ставка дисконтирования, а процесс определения PV называют дисконтированием.

В этих расчетах легко представить себе, что будущие поступления и есть то самое движение денежных средств, которое мы хотим прогнозировать. Для начала рассчитаем настоящую стоимость однократного будущего вложения. Это можно сделать, если известна сумма будущего вклада FV, ставка дисконтирования r и число периодов начисления m.

Графическое представление процессов дисконтирования и приведения (наращения) денежной суммы (1 рубля) показано ниже:

   PV руб.                                                              FV руб.

       1,0             r=0 %                                            4              x

       0,8                                                                                                         

                                                                              3               r=100 %     

      0,5 х                                                                                                        

      0,3        r=100 %                                              2     х    r=0 %

      0,25 х                                                         

                                                                                          1

0 I I I      I                                                                     I   I  I        I 

      1 2 3 ... t                                                            0  1    2 3 ...     t

Очевидно, что PV денежной суммы тем меньше, чем выше r и больше t (число дисконтируемых периодов); напротив, FV тем больше, чем больше r и число дисконтируемых периодов t.

Ставка дисконтирования

Дисконт (ставка процента) может рассматриваться как альтернативная стоимость денег.

Если, к примеру, имеется альтернатива — положить деньги в банк, то альтернативная стоимость dаших денег – это проценты, которые заплатил бы Вам банк.

В простой модели экономики с двумя периодами и индивидуумами, которые берут и дают ссуду, альтернативная стоимость получается равной и для того, кто дает деньги в долг, и для того, кто берет их. В последнем случае мы говорили о проценте.

В реальной жизни ставка дисконтирования не всегда совпадает с процентом. Почему? Влияет риск. Часто срок будущего вклада не столь определен, инвестор (и получатель) не всегда уверен в этом вложении (платеже). Все эти факторы могут повлиять на значение альтернативной стоимости. Мы рассмотрим эту тему более подробно в главе «Риск и доход».

Как и в случае расчета будущей стоимости, на настоящую стоимость будущего вложения могут повлиять три фактора – размер ожидаемого вложения, ставка процента, период инвестирования. Рассмотрим следующий пример.

Пример 7: 31 декабря 2013 г. вкладчик решил инвестировать 1000 д.е. в дело, которое, как он ожидает, принесет ему через год 1500 д.е. Чему равна ожидаемая доходность такой инвестиции?

В данном случае доходность равна ставке дисконтирования. Давайте сначала рассчитаем ставку дисконтирования, а потом подумаем, почему она равна ставке доходности. Для решения этой проблемы подставим все известные значения в уравнение 1.5 и найдем r:

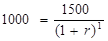
После решения уравнения получаем r = 50 %. Теперь посмотрим, почему эта ставка дисконтирования равна ожидаемой доходности. Если вложить 1000 д.е. под 50 % на один год, то через год вы получите 1500 д.е.. Но мы используем термин ожидаемый доход, чтобы подчеркнуть, что это доход, который мы сегодня, 31 декабря, ожидаем получить через год.

Аннуитеты

Аннуитет представляет собой ровный поток регулярных денежных выплат (доходов или расходов) в течение определенного периода времени. Аннуитеты являются одним из самых распространенных типов финансовых инструментов. Пенсии, которые люди получают, часто принимают форму аннуитета, например, ежемесячного фиксированного платежа. Выплаты по купонным облигациям, которые могут производиться дважды в год или ежеквартально, также носят форму аннуитетов.

Существует три типа аннуитетов:– обычный аннуитет с выплатами (C) в конце периода (ordinary annuity), аннуитет с выплатами в начале периода (annuity due) и бесконечный аннуитет (перпетуитет).

Единственная разница между обычным аннуитетом и аннуитетом с выплатами в начале периода заключается во времени начального платежа. Построим Time-line для этих двух типов аннуитетов, чтобы объяснить это различие.

Обычный аннуитет

 0                                  1                      2               3

                                C                            C                     C

Аннуитет с выплатами в начале периода

0                                  1                     2               3

        C                                   C                                           C

На этих графиках видно, что в первом случае платежи осуществляются в конце периода, а во втором случае – в начале периода. Число платежей в каждом случае одно и то же. Выплата в начале периода увеличивает число дисконтируемых период на один, т.е.:

PV(annuity due) = PV(ordinary annuity)*(1+r)

FV(annuity due) = FV(ordinary annuity)*(1+r)

В результате выплата в начале периода увеличивает размер как PV, так и FV.

Если платежи продолжаются бесконечно, мы имеем дело с бесконечным аннуитетом (перпетуитетом). Ниже мы увидим, как определить будущую и настоящую стоимость аннуитета в каждом случае.