Докажем теперь формулу для производной однородного полинома 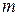 -й степени при симметричной матрице коэффициентов А.
-й степени при симметричной матрице коэффициентов А.
Если матрица  в которой мультииндексы
в которой мультииндексы  содержат по
содержат по  индексов, а мультииндекс
индексов, а мультииндекс 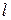 произвольное число индексов, симметрична относительно мультииндексов
произвольное число индексов, симметрична относительно мультииндексов  , то
, то
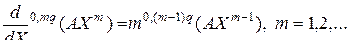 . (3.2.38)
. (3.2.38)
Доказательство формулы (3.2.38) выполним по индукции. Для 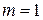 и
и 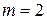 она справедлива (см. формулы (3.2.26), (3.2.31)). Найдем производную функции
она справедлива (см. формулы (3.2.26), (3.2.31)). Найдем производную функции
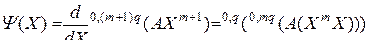
как производную произведения. Получим
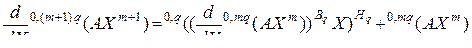 . (3.2.39)
. (3.2.39)
Подставив сюда производную (3.2.38), будем иметь
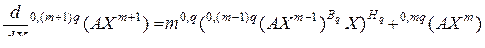 .
.
Докажем, что
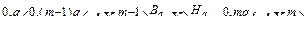 . (3.2.40)
. (3.2.40)
Для того чтобы выполнялось умножение  и равенство (3.2.39), матрицу
и равенство (3.2.39), матрицу 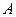 в процессе доказательства необходимо предположить имеющей вид
в процессе доказательства необходимо предположить имеющей вид  , где мультииндексы
, где мультииндексы 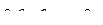 содержат по
содержат по  индексов, мультииндекс
индексов, мультииндекс 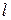 содержит произвольное количество индексов, и матрица
содержит произвольное количество индексов, и матрица  симметрична относительно мультииндексов
симметрична относительно мультииндексов  . Доказательство равенства (3.2.40) проведем для случая, когда
. Доказательство равенства (3.2.40) проведем для случая, когда  ,
,  ,
,  . С учетом принятых обозначений для правой и левой частей равенства (3.2.40) получим
. С учетом принятых обозначений для правой и левой частей равенства (3.2.40) получим
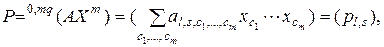 (3.2.41)
(3.2.41)
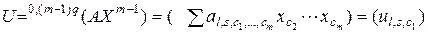 ,
,
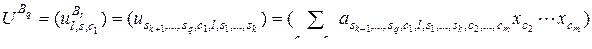 ,
,
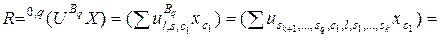
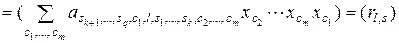 ,
,
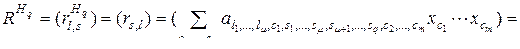
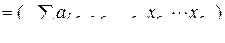 . (3.2.42)
. (3.2.42)
Мы видим, что если матрица  симметрична относительно мультииндексов
симметрична относительно мультииндексов 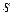 и
и  , то матрицы
, то матрицы 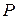 (3.2.41) и
(3.2.41) и 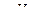 (3.2.42) равны. Аналогично можно доказать равенство (3.2.40) и для случая, когда мультииндекс
(3.2.42) равны. Аналогично можно доказать равенство (3.2.40) и для случая, когда мультииндекс 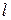 в матрице
в матрице  содержит
содержит 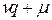 индексов,
индексов, 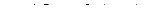 Таким образом мы доказали, что из формулы для производной
Таким образом мы доказали, что из формулы для производной 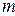 -й степени
-й степени  следует такая же формула для производной
следует такая же формула для производной 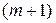 -й степени
-й степени  . Доказательство формулы (3.2.38) закончено.
. Доказательство формулы (3.2.38) закончено.
Производные высших порядков однородного полинома произвольной степени
Применяя последовательно формулу (3.2.38), получим производные более высоких порядков однородного полинома 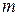 -й степени при симметричной матрице коэффициентов
-й степени при симметричной матрице коэффициентов  :
:
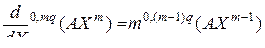 , (3.2.43)
, (3.2.43)
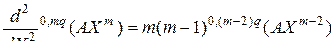 , (3.2.44)
, (3.2.44)
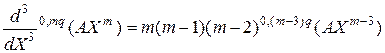 , (3.2.45)
, (3.2.45)
и вообще
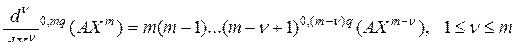 . (3.2.46)
. (3.2.46)
В частности, при 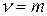 получаем
получаем
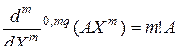 . (3.2.47)
. (3.2.47)
Формулы (3.2.43) – (3.2.47) показывают, что имеется впечатляющая аналогия между многомерно-матричным дифференцированием и скалярным дифференцированием.
3.2.12. Производная 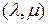 -обратной матрицы
-обратной матрицы
Матрица 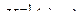 ,
, 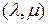 -обратная к
-обратная к  -мерной матрице
-мерной матрице  -го порядка
-го порядка  относительно
относительно 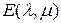 , является функцией исходной матрицы
, является функцией исходной матрицы  , и поэтому естественно говорить о производной обратной матрицы. Она определяется формулой
, и поэтому естественно говорить о производной обратной матрицы. Она определяется формулой
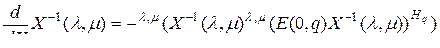 . (3.2.48)
. (3.2.48)
Для доказательства обозначим  и воспользуемся соотношением (см. формулу (2.5.2))
и воспользуемся соотношением (см. формулу (2.5.2))
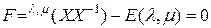 .
.
По правилу неявного дифференцирования (3.2.18) получим уравнение
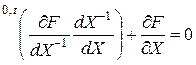 ,
,  . (3.2.49)
. (3.2.49)
Так как
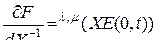 ,
, 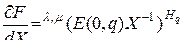 ,
,
то, подставив эти выражения в уравнение (3.2.49), получим
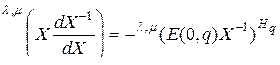 .
.
Умножая обе части последнего равенства слева на матрицу  в смысле
в смысле 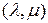 -свернутого произведения, получаем формулу (3.2.48).
-свернутого произведения, получаем формулу (3.2.48).
3.2.13. Производная 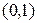 -обратной двухмерной матрицы
-обратной двухмерной матрицы
Пусть  – двухмерная матрица
– двухмерная матрица  -го порядка и
-го порядка и  –
– 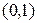 -обратная к
-обратная к
ней матрица относительно 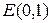 . Тогда
. Тогда
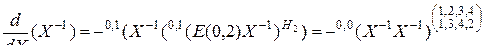 , (3.2.50)
, (3.2.50)
где для краткости обозначено  . Эта формула является частным случаем формулы (3.2.48) при
. Эта формула является частным случаем формулы (3.2.48) при  .
.
Дата: 2019-02-02, просмотров: 498.