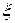Определение. Начальным моментом -го порядка случайной матрицы  (4.1) называется математическое ожидание -й 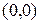-свернутой степени матрицы :

,

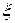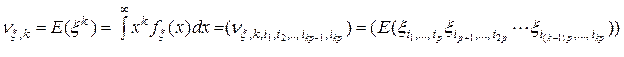.                                     (4.2)

Очевидно, что начальный момент первого порядка есть среднее значение или математическое ожидание случайной многомерной матрицы ,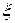

.

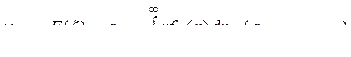Математическое ожидание случайной многомерной матрицы 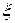 обладает свойствами, аналогичными свойствам математического ожидания скалярной случайной величины. Так, если

,

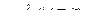где 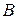 – матрица коэффициентов, то

.                       (4.3)

Действительно, по определению 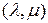-свернутого произведения и свойству математического ожидания суммы получим

.

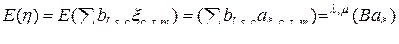Определение. Центральным моментом -го порядка случайной матрицы

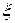
 (4.1) называется математическое ожидание -й 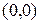-свернутой степени матрицы :

,

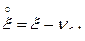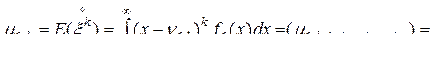
.                                      (4.4)

Очевидно, что центральный момент второго порядка есть дисперсионная матрица случайной многомерной матрицы ,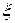

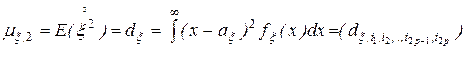.    (4.5)

Дисперсионная матрица случайной многомерной матрицы 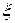 имеет следующее свойство. Если -мерная случайная матрица 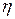 определяется равенством

,

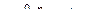где 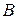 – 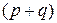-мерная матрица коэффициентов, то

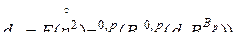.                           (4.6)

Действительно, поскольку , то

.

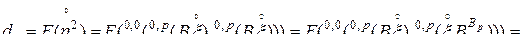
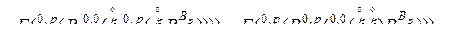
Понятно, что дисперсионная матрица -мерной случайной матрицы 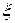 – это 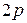-мерная матрица вида

,

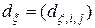симметричная относительно своих -мультииндексов 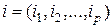 и .

Из приведенных выше определений видно, что момент -го порядка -мерной матрицы является 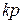-мерной матрицей -го порядка вида

,

симметричной относительно своих -мультииндексов .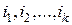

По начальным моментам случайной матрицы 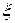 (4.1) до порядка  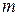включительно можно получить центральные моменты до порядка  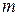и наоборот. Однако общую формулу связи, как в скалярном случае [66], записать трудно, поэтому рассмотрим лишь частные случаи. Поскольку

,

то

,

.

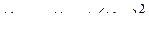Раскроем теперь выражение для центрального момента третьего порядка,

.

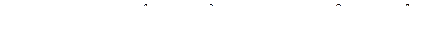
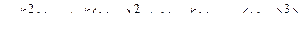Отсюда получаем, что

,

.

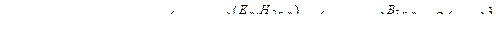Определение. Случайная -мерная матрица -го порядка 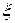 (4.1), плотность вероятности которой задается выражением

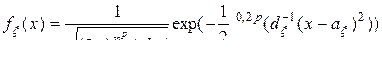,            (4.7)

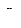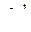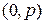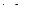
называется гауссовской или нормальной случайной матрицей. В приведенном выражении ,  – параметры гауссовского матричного распределения, причем  – математическое ожидание или начальный момент первого порядка,  – дисперсионная матрица или центральный момент второго порядка,  – матрица, -обратная к , – определитель матрицы , под которым понимается определитель матрицы, 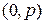-ассоциированной с матрицей  (раздел 2.3).

Теорема 4.1 (о ассоциированных случайных матрицах). Пусть 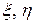 – случайные -мерная и -мерная матрицы -го порядка соответственно, связанные между собой зависимостью

,

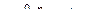где 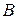 – 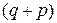-мерная матрица коэффициентов, ,  – математические ожидания этих матриц, ,  – их ковариационные матрицы, 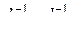 – матрицы, 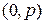- и 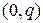-обратные ковариационным, и 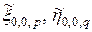, , 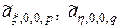, , 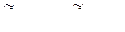 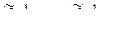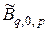– ассоциированные с вышеприведенными матрицами матрицы. Тогда справедливы следующие отношения эквивалентности:

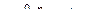
,                           (4.8)

,                        (4.9)

.  (4.10)

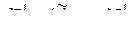.                                    (4.11)

Доказательство теоремы. Соотношения (4.8) вытекают из теоремы 2.2 о ассоциированных матрицах раздела 2.3. Соотношения (4.9) вытекают из свойства математического ожидания (4.3) и теоремы 2.2. Соотношения (4.10) вытекают из свойства ковариационной матрицы (4.6) и теоремы 2.2. Осталось доказать соотношения (4.11). По определению 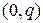-обратной матрицы имеем равенство

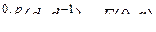.                               (4.12)

По теореме 2.2 справедливо эквивалентное равенство для ассоциированных матриц

,

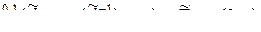где 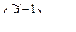 – матрица, 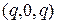-ассоциированная с матрицей 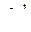,  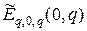– матрица, 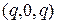-ассоциированная с матрицей 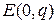. Учитывая, что , вместо (4.12) получим эквивалентное равенство

.

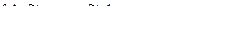Отсюда заключаем, что

,

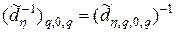т.е.

.

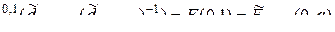Последнее равенство свидетельствует, что матрица 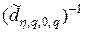 является 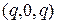-ассоциированной с матрицей 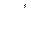, что и требовалось доказать.