Рассмотрим сначала векторный случайный процесс 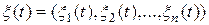 с дискретным временем, который будем обозначать как
с дискретным временем, который будем обозначать как
 ,
,  . (10.2.28)
. (10.2.28)
Определение. Случайный процесс 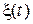 называется Марковским, если для него выполняется равенство
называется Марковским, если для него выполняется равенство
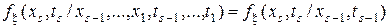 . (10.2.281)
. (10.2.281)
Условная плотность вероятности  называется плотностью вероятности перехода Марковского процесса.
называется плотностью вероятности перехода Марковского процесса.
Определим процесс (10.2.28) соотношением
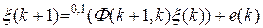 ,
, 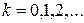 , (10.2.29)
, (10.2.29)
где 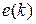 – последовательность независимых нормально распределенных векторов,
– последовательность независимых нормально распределенных векторов,
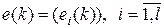 ,
,
с нулевыми средними значениями и ковариационными матрицами
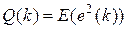 , (10.2.30)
, (10.2.30)
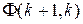 – двухмерная
– двухмерная 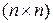 -матрица,
-матрица,
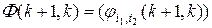 ,
, 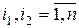 ,
,
с зависящими от  элементами. Векторы
элементами. Векторы 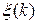 и
и 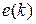 являются независимыми. Начальное состояние
являются независимыми. Начальное состояние 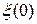 предполагаем нормальным с математическим ожиданием
предполагаем нормальным с математическим ожиданием
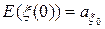 (10.2.31)
(10.2.31)
и ковариационной матрицей
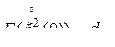 . (10.2.32)
. (10.2.32)
Относительно такого процесса справедлива следующая теорема [70].
Теорема 10.8. Если векторный случайный процесс с дискретным временем 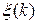 (10.2.29) описывается соотношением (10.2.29), в котором
(10.2.29) описывается соотношением (10.2.29), в котором 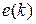 – последовательность независимых гауссовских случайных векторов
– последовательность независимых гауссовских случайных векторов  с нулевыми средними значениями и ковариационными матрицами
с нулевыми средними значениями и ковариационными матрицами 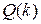 (10.2.30), векторы
(10.2.30), векторы 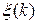 и
и 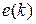 независимы, начальное состояние
независимы, начальное состояние 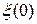 гауссовское со средним значением
гауссовское со средним значением 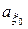 (10.2.31) и ковариационной матрицей
(10.2.31) и ковариационной матрицей 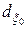 (10.2.32), то такой процесс является гауссовским марковским со средним значением
(10.2.32), то такой процесс является гауссовским марковским со средним значением
 ,
, 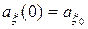 , (10.2.33)
, (10.2.33)
ковариационной функцией
 , (10.2.34)
, (10.2.34)
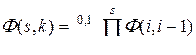 ,
,
и ковариационной матрицей

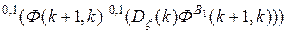 ,
, 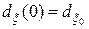 . (10.2.35)
. (10.2.35)
Эти понятия обобщаются на многомерно-матричные случайные процессы. Рассмотрим 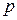 -мерно-матричный случайный процесс (1) с дискретным временем, который будем обозначать как
-мерно-матричный случайный процесс (1) с дискретным временем, который будем обозначать как 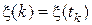 .
.
Определение Марковского многомерно-матричного случайного процесса не изменяется, т.е. имеет вид (10.2.281).
Определим теперь 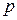 -мерно-матричный случайный процесс
-мерно-матричный случайный процесс 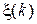 соотношением
соотношением
 ,
, 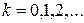 , (10.3.15)
, (10.3.15)
где 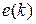 – последовательность независимых нормально распределенных
– последовательность независимых нормально распределенных 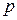 -мерных матриц с нулевыми средними значениями и дисперсионными матрицами
-мерных матриц с нулевыми средними значениями и дисперсионными матрицами
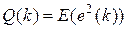 , (10.3.16)
, (10.3.16)
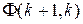 –
– 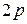 -мерная матрица, в общем случае зависящая от
-мерная матрица, в общем случае зависящая от  . Матрицы
. Матрицы 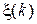 и
и 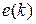 являются независимыми. Начальное состояние
являются независимыми. Начальное состояние 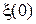 предполагаем нормальным с математическим ожиданием
предполагаем нормальным с математическим ожиданием
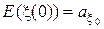 (10.3.17)
(10.3.17)
и дисперсионной матрицей
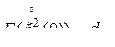 . (10.3.18)
. (10.3.18)
Относительно такого процесса можно доказать следующую теорему.
Теорема 10.10. Если 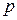 -мерно-матричный случайный процесс с дискретным временем
-мерно-матричный случайный процесс с дискретным временем 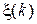 описывается соотношением (10.3.15), в котором
описывается соотношением (10.3.15), в котором 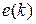 – последовательность независимых гауссовских случайных матриц
– последовательность независимых гауссовских случайных матриц  с нулевыми средними значениями и ковариационными матрицами
с нулевыми средними значениями и ковариационными матрицами 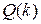 (10.3.16), матрицы
(10.3.16), матрицы 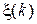 и
и 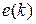 независимы, начальное состояние
независимы, начальное состояние 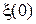 гауссовское со средним значением
гауссовское со средним значением 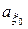 (10.3.17) и ковариационной матрицей
(10.3.17) и ковариационной матрицей 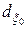 (10.3.18), то такой процесс является гауссовским марковским со средним значением
(10.3.18), то такой процесс является гауссовским марковским со средним значением
 ,
, 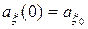 , (10.3.19)
, (10.3.19)
ковариационной функцией
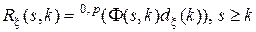 , (10.3.20)
, (10.3.20)
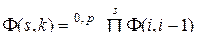 ,
,
и дисперсионной матрицей

 ,
, 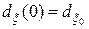 . (10.3.21)
. (10.3.21)
Эта теорема может быть доказана путем перехода от исходных матриц в постановке задачи к соответствующим ассоциированным матрицам, записи выражений (10.2.33)–(10.2.35) для ассоциированных матриц и перехода от них к эквивалентным многомерно-матричным выражениям (10.3.19)–(10.3.21) на основе теоремы о ассоциированных матрицах.
Скалярные случайные поля
Пусть задано некоторое вероятностное пространство 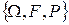 .
.
Определение. Скалярным случайным полем
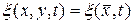 (10.4.1)
(10.4.1)
называется действительная скалярная функция 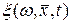 , которая для любых фиксированных аргументов
, которая для любых фиксированных аргументов 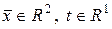 является измеримой функцией
является измеримой функцией 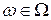 .
.
Аргумент 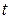 в этом определении понимается как время, а аргумент
в этом определении понимается как время, а аргумент 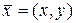 – как точка плоскости.
– как точка плоскости.
Если в трехмерном пространстве переменных 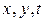 зафиксировать
зафиксировать  точек
точек
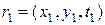 ,
, 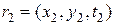 , …,
, …, 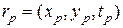 , (10.4.2)
, (10.4.2)
то получим  случайных величин – сечений случайного поля
случайных величин – сечений случайного поля
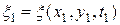 ,
, 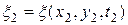 , … ,
, … , 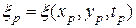 .
.
Распределение случайного вектора  при любом
при любом  и любых наборах точек
и любых наборах точек 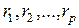 (10.4.2) назовем конечномерным (
(10.4.2) назовем конечномерным (  -мерным) распределением скалярного случайного поля.
-мерным) распределением скалярного случайного поля.
Определение. Конечномерной (  -мерной) функцией распределения скалярного случайного поля
-мерной) функцией распределения скалярного случайного поля  (10.4.1) назовем функцию распределения
(10.4.1) назовем функцию распределения  -мерного случайного вектора
-мерного случайного вектора  :
:
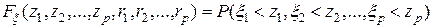 ,
,
где 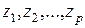 ,
, 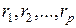 - аргументы функции распределения.
- аргументы функции распределения.
Определение. Конечномерной (  -мерной) плотностью вероятности скалярного случайного поля
-мерной) плотностью вероятности скалярного случайного поля  (10.4.1) называется функция
(10.4.1) называется функция
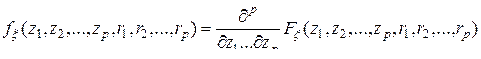
Замечание. Конечномерные (  -мерные) функция распределения и плотность вероятности случайного поля зависят от
-мерные) функция распределения и плотность вероятности случайного поля зависят от  точек плоскости
точек плоскости 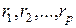 (10.4.2), на которых рассматриваются случайные величины
(10.4.2), на которых рассматриваются случайные величины 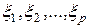 .
.
Определение. Математическим ожиданием случайного поля  (10.4.1) в точке
(10.4.1) в точке 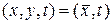 называется функция
называется функция 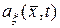 , определяемая выражением
, определяемая выражением
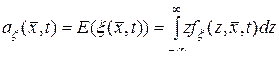 , (10.4.3)
, (10.4.3)
где 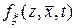 – одномерная плотность вероятности случайного поля.
– одномерная плотность вероятности случайного поля.
Определение. Дисперсией случайного поля  (10.4.1) в точке
(10.4.1) в точке 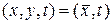 называется функция
называется функция 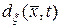 , определяемая выражением
, определяемая выражением
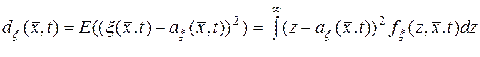 . (10.4.4)
. (10.4.4)
Определение. Ковариационной функцией случайного поля  (10.4.1) называется функция, определяемая выражением
(10.4.1) называется функция, определяемая выражением
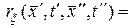
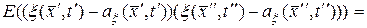
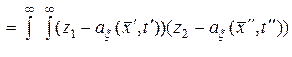
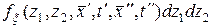 , (10.4.5)
, (10.4.5)
где 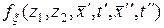 – двухмерная плотность вероятности случайного поля.
– двухмерная плотность вероятности случайного поля.
Ковариационная функция случайного поля обладает тем свойством, что
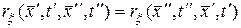 .
.
Дисперсия случайного поля может быть получена по его ковариационной функции,
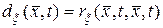 .
.
Определение. Конечномерным (  -мерным) математическим ожиданием случайного поля
-мерным) математическим ожиданием случайного поля  (10.4.1) на системе из
(10.4.1) на системе из  точек называется
точек называется  -мерный вектор
-мерный вектор 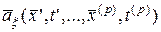 , являющийся математическим ожиданием вектора
, являющийся математическим ожиданием вектора  :
:
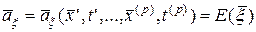 . (10.4.6)
. (10.4.6)
Определение. Ковариационной матрицей случайного поля  (10.4.1) на системе из
(10.4.1) на системе из  точек называется
точек называется 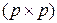 -матрица
-матрица 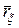 , которая является ковариационной матрицей вектора
, которая является ковариационной матрицей вектора  :
:
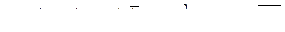 .
.
Элементы ковариационной матрицы могут быть получены по известной ковариационной функции с помощью формулы
 .
.
Определение. Случайное поле  (10.4.1) называется стационарным в узком смысле, если для любого
(10.4.1) называется стационарным в узком смысле, если для любого 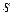
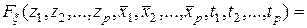
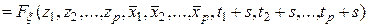 ,
,
где  –
–  -мерная функция распределения случайного поля.
-мерная функция распределения случайного поля.
Определение. Случайное поле  (10.4.1) называется стационарным в широком смысле, если его математическое ожидание не зависит от времени,
(10.4.1) называется стационарным в широком смысле, если его математическое ожидание не зависит от времени,
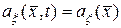 ,
,
а ковариационная функция зависит лишь от одного аргумента 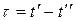 ,
,
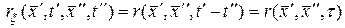 .
.
Ковариационная функция стационарного случайного поля обладает следующим
свойством:
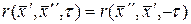 .
.
Определение. Случайное поле  (10.4.1) называется однородным в широком смысле, если для двух точек пространства аргументов
(10.4.1) называется однородным в широком смысле, если для двух точек пространства аргументов 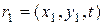 ,
, 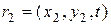 выполняются равенства
выполняются равенства
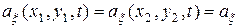 ,
,
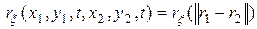 ,
,
где 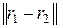 – расстояние между точками
– расстояние между точками 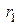 и
и 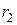 .
.
Определение. Случайное поле  (10.4.1) называется гауссовским, если все его конечномерные распределения гауссовские.
(10.4.1) называется гауссовским, если все его конечномерные распределения гауссовские.
Если случайное поле в момент времени 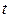 измеряется на сетке (матрице)
измеряется на сетке (матрице)  значений аргументов
значений аргументов 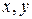 ,
,
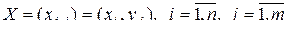 ,
,
то значения поля образуют двухмерную случайную матрицу
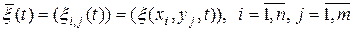 .
.
Математическим ожиданием случайного поля на сетке значений аргументов будет также двухмерная матрица
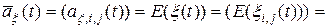
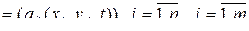 .
.
Ковариационная матрица случайного поля на сетке значений аргументов будет представлять собой четырехмерную 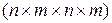 -матрицу
-матрицу
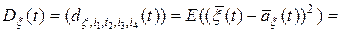
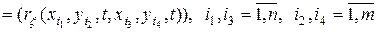 .
.
Плотность вероятности гауссовского случайного поля на сетке значений аргументов имеет вид
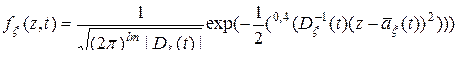 , (10.4.7)
, (10.4.7)
где 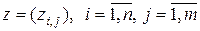 , – матричный аргумент плотности вероятности,
, – матричный аргумент плотности вероятности, 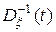 – матрица,
– матрица, 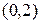 -обратная к
-обратная к 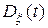 ,
, 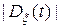 – определитель матрицы
– определитель матрицы 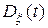 .
.
В практических приложениях чаще всего предполагается, что известна ковариационная функция случайного поля [122]. Часто используется ковариационная функция поля вида [17]
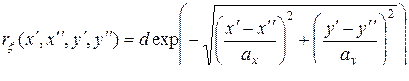 ,
,
где 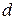 – дисперсия поля,
– дисперсия поля, 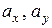 – параметры, характеризующие коррелированность поля в горизонтальном и вертикальном направлениях. В задачах фильтрации изображений иногда используется ковариационная функция вида [97]
– параметры, характеризующие коррелированность поля в горизонтальном и вертикальном направлениях. В задачах фильтрации изображений иногда используется ковариационная функция вида [97]
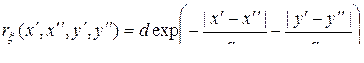 .
.
Дата: 2019-02-02, просмотров: 558.