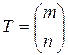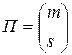Часто матрицу приходится транспонировать дважды в соответствии с подстановками  и . Очевидно, тот же результат можно получить транспонированием матрицы один раз соответственно некоторой новой подстановке 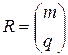. Здесь мультииндексы из набора индексов 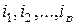, причем 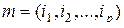. Необходимо уметь находить результирующую подстановку 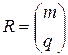. Решение этой задачи дается следующей теоремой.

Теорема 2.3 (о повторном транспонировании). Равенство

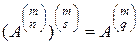                                        (2.9.9)

для произвольной матрицы 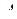 выполняется тогда и только тогда, когда подстановк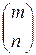и  и 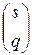 эквивалентны.

Доказательство. Пусть равенство (2.9.9) выполняется. Тогда, обозначив

,

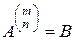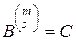,                                          (2.9.10)

,

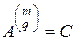и пользуясь определением транспонирования матрицы (2.8.7), получим

,

,

.

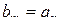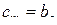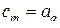Из последних двух равенств вытекает, что

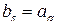
или, что то же,

.

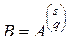Так как справедливо также первое из равенств (2.9.10), то

,

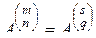что означает эквивалентность подстановок 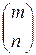 и .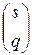

Пусть теперь подстановк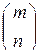и  и 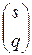 эквивалентны. Тогда вместо левой части равенства (2.9.9) будем иметь выражение

.

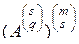Обозначив здесь

,

,

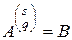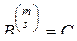получим

,                                           (2.9.11)

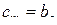,                                          (2.9.12)

откуда следует, что

,

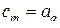или

.

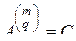Мы получили правую часть равенства (2.9.9), т.е. это равенство выполняется. Теорема доказана.

Приведенная теорема дает правило нахождения результирующей подстановки 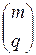 при повторном транспонировании матрицы 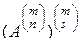. Верхняя строка подстановки известна: 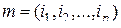. Нижняя строка находится следующим образом. Записываем подстановку  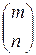в рангах. Такую же запись в рангах должна иметь и подстановка 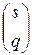. Нумеруем индексы известной строки  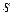этой подстановки по порядку, т. е. получаем запись строки  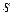в рангах. Нижняя строка  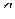в рангах имеет тот же вид, что и строка . 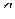Записываем строку  в индексах путем замены рангов соответствующими индексами из строки .

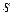Пример 2.6. Найдем итоговую подстановку 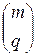 при повторном транспонировании четырехмерной матрицы соответственно подстановкам

.

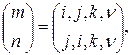
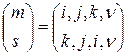В соответствии с теоремой о повторном транспонировании матрицы подстановка 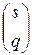 в рангах должна быть такой же, как и подстановка  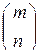в рангах. Получаем, что

.

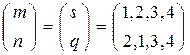Так как по условию 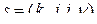, то , , 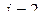, , 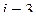, 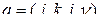и искомая подстановка имеет вид

.

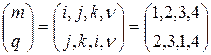Способ повторного транспонирования, содержащийся в приведенной теореме, представляется неудобным. Можно предложить более простой способ как следствие из теоремы.

Следствие. При повторном транспонировании многомерной матрицы (2.9.9) итоговая подстановка 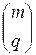 равна суперпозиции подстановок  и :

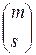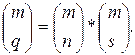
                                       (2.9.13)

Действительно, равенства (2.9.11) и (2.9.12) означают преобразование матрицы 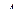 в матрицу 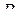, затем матрицы  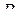в матрицу 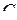. При этом происходит следующее отображение мультииндексов: 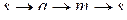. Это означает суперпозицию подстановок  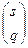и 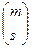, а значит и подстановок  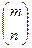и 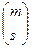 в силу эквивалентност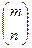и  и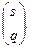

Пример 2.7. Рассмотрим подстановки предыдущего примера

, ,

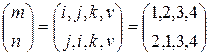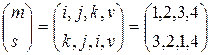и найдем итоговую подстановку как суперпозицию этих подстановок:

.

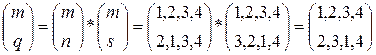Видим, что суперпозиция совпадает с подстановкой 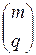, полученной в предыдущем примере другим способом.

В заключение отметим, что в соответствии с правилом повторного транспонирования матрицы справедливо равенство

.

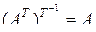Точно также

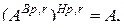
так как подстановк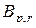и  и 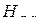 взаимно обратные.