Вопрос транспонирования многомерных матриц является более сложным по сравнению с транспонированием обычных (двухмерных) матриц. Данный раздел посвящен разработке этого вопроса.

Пусть 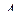 – 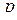-мерная матрица 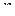-го порядка,

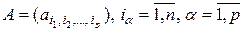.                         (2.8.1)

Новая матрица

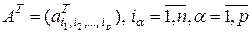,                         (2.8.2)

элементы которой связаны с элементами матрицы 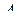 (2.8.1) соотношениями

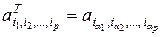,                                    (2.8.3)

где 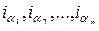 – какая-нибудь перестановка из индексов 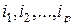, называется транспонированной относительно матрицы  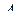соответственно подстановке

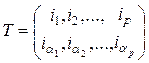.                                      (2.8.4)

Транспонированную матрицу будем обозначать одним из символов

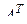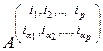, .                                   (2.8.5)

Пример 2.5. Пусть 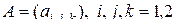, и подстановка 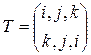. Тогда

,

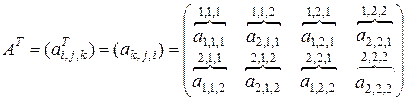где числами над фигурными скобками указаны значения мультииндекса 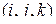 матрицы .

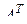Приведенное определение транспонирования многомерной матрицы принадлежит Соколову Н.П. [81]. Однако Соколовым Н.П. не введены формальные правила работы с транспонированными матрицами, что является, по-видимому, одной из причин недостаточного использования аппарата многомерных матриц. Эти правила приводятся в данном разделе [51].

Подстановкой (или перестановкой)

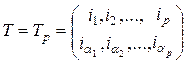
называется взаимно однозначное отображение (биекция) множества индексов 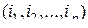 на себя [24]. Это отображение множеству индексов  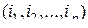ставит в соответствие множество индексов 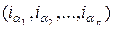, так что .

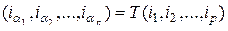Любую подстановку, заданную на множестве 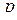 индексов, будем обозначать прописной буквой, например, 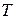, как это сделано в выражении (2.8.4). Чтобы подчеркнуть, что подстановка состоит из  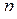индексов, будем применять также обозначение 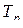. Будем пользоваться понятием мультииндексов [51]

,

,

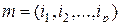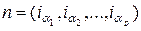и записывать подстановку (2.8.4) в виде

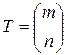.                                              (2.8.6)

С использованием мультииндексов транспонирование матрицы будем обозначать следующим образом. Если 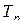 – подстановка вида (2.8.6), то запись вида

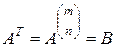
означает выполнение равенств

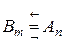.                                             (2.8.7)

Заметим, что транспонирование матрицы 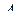 (2.8.7) задается двумя отображениями: матрицы  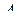в матрицу  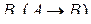и верхнего мультииндекса  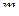в нижний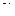 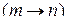. Эти отображения обозначены в (2.8.7) стрелками в противоположных направлениях.

Часто подстановку (2.8.4) удобно разбить на несколько подстановок. Такое разбиение будем обозначать одним из следующих способов

.

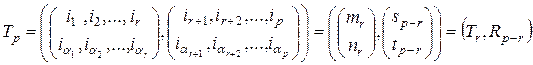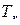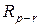Ясно, что входящие в разбиение подстановки  и  должны быть определены на различных множествах индексов.

Есл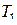и  и 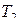 – две подстановки,

, ,

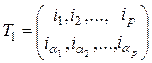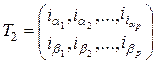где 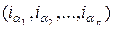,  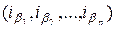– некоторые перестановки множества 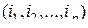, то подстановка 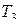, действующая согласно выражению

,

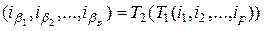называется суперпозицией подстановок 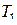 и 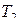 и обозначается как

.

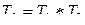Это определение аналогично определению суперпозиции функций. Нахождение суперпозиции подстановок состоит в последовательном прослеживании преобразований (отображений) индексов. Например,

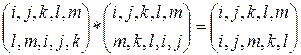.                     (2.8.8)

В частности, первый индекс  первой подстановки отображается (преобразуется) в индекс 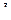, затем индекс  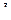второй подстановки преобразуется в индекс . В итоге индекс  преобразуется в индекс .

Будем пользоваться понятиями тождественной и обратной подстановок, имеющимися, например, в [24], и введем несколько новых типов подстановок [51].

Тождественной подстановкой на 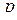 индексах называется подстановка вида [24]

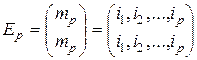.                                  (2.8.9)

Она удовлетворяет равенствам

,

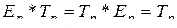где 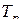 – произвольная подстановка, заданная на том же множестве индексов, что и 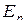, а символами  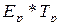обозначена суперпозиция подстановок  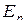и .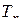

Обратной подстановкой для подстановки 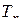 называется подстановка 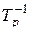, удовлетворяющая равенствам [24]

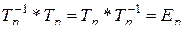.                               (2.8.10)

Подстановкой типа “вперед” назовем подстановку вида [51]

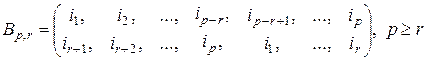,       (2.8.11)

в которой нижняя строка формируется из верхней переносом 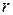 левых индексов вправо (вперед).

Аналогично подстановкой типа “назад” назовем подстановку вида

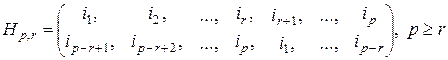,     (2.8.12)

в которой нижняя строка формируется из верхней переносом 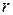 правых индексов влево (назад).

Ясно, что 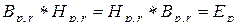, т.е. подстановк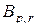и  и 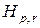 – взаимно обратны,

.

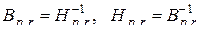Пр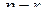и  или  имеем

, .

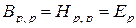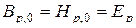Ясно также, что подстановки типа "вперед" и "назад" взаимозаменяемы:

, .

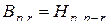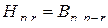Подстановкой типа “вперед-назад” назовем подстановку вида

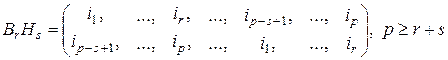,           (2.8.13)

в которой нижняя строка формируется из верхней переносом 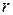 левых индексов вправо (вперед) и  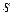правых индексов влево (назад). При  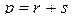 (центральные индексы отсутствуют) имеем

.

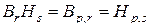При  или  получаем

.

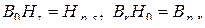Примерами подстановок типа “вперед”, “назад”, “вперед-назад” могут быть подстановки

, , .

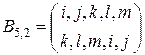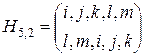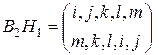Перейдем к операции транспонирования матрицы в соответствии с некоторой подстановкой. Напомним, что в определении 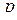-мерной матрицы  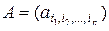(2.8.1) индексы  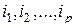являются координатами 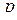-мерного пространства, в котором рассматривается матрица 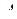. В этом же пространстве рассматриваются и все матрицы, получающиеся из  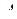путем транспонирования. Это значит, что все транспонированные матрицы имеют те же индексы, что и исходная матрица: 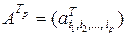. Индексы этого основного пространства, в котором определена матрица 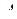, нумеруются по порядку от 1 до 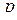, т.е. каждому индексу присваивается порядковый номер (ранг). Если заменить в подстановке  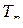индексы их номерами (рангами), то мы получим вместо индексной записи подстановки  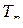ее новую запись, которую назовем ранговой. Ранговая запись содержит всю информацию о подстановке и во многих случаях более удобна по сравнению с индексной. Пользуясь подстановкой в рангах, удобно переходить от одной системы индексов к другой. Можно переставлять столбцы подстановки без опасения потерять последовательность координат основного пространства. Однако полностью отказаться от индексной записи подстановки нельзя, так как обозначения  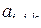и 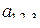 имеют различный смысл: в первом случае это вся совокупность элементов матрицы 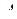, во втором случае – один элемент со значениями индексов .

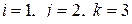Подстановки, имеющие одну и ту же запись в рангах, назовем эквивалентными (равными по действию на матрицу). Так, подстановки

,

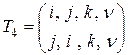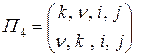
эквивалентны, поскольку в рангах они имеют одну и ту же запись

.

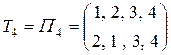Если подстановк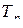и  и 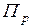 эквивалентны, то для любой 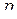-мерной матрицы  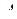выполняется равенство

,

которое означает, что транспонирование матрицы может быть задано с помощью одной из эквивалентных подстановок.

 Поскольку любая транспонированная матрица 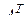 рассматривается в том же пространстве, в котором определена исходная матрица  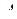(в исходном пространстве), то в качестве верхней строки любой подстановки будем использовать строку  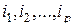в обозначении матрицы  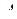(2.8.1).