Впервые систематические методы расчета матричных производных были предложены в работе [111], хотя примеры матричных производных встречались и ранее. Так, в работе [112] получена производная квадратичной формы 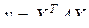 с симметричной матрицей  по вектору-столбцу , которая равна 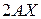. В работе [111] даны определения производной матричной функции  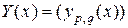по скалярной переменной ,

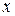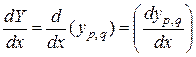                                      (3.1.1)

и производной скалярной функции 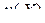 по матрице ,

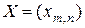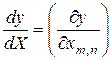.                                               (3.1.2)

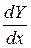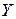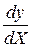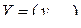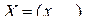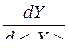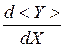Как видно из определений (3.1.1), (3.1.2), указанные производные являются матрицами, причем  – матрица тех же размеров, что и , а  – матрица тех же размеров, что и . Для дифференцирования матрицы  по матрице  авторы вводят два вида производных:  и . Производная

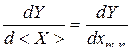                                            (3.1.3)

при фиксированных значениях индексов 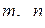 представляет собой производную типа (3.1.1), т. е. матрицу тех же размеров, что и 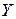. Производная

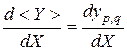                                              (3.1.4)

при фиксированных значениях индексов 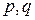 есть производная типа (3.1.2), т.е. матрица тех же размеров, что и . На основе этих определений в [111] получены производные некоторых матричных функций. Так, для функций 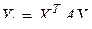,  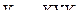матричного аргумента  получены производные

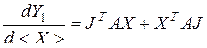,                                     (3.1.5)

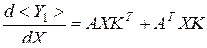,                                     (3.1.6)

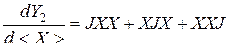,                                (3.1.7)

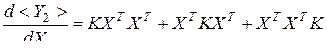.            (3.1.8)

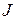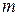В формулах (3.1.5) – (3.1.8)  – матрица тех же размеров, что и , все элементы которой равны нулю, кроме единицы на пересечении -й строки и -го столбца. Матрица 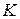 имеет те же размеры, что и матрица 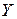, и все нулевые элементы, кроме единицы на пересечении -й строки и 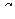-го столбца.

Заметим, что формулы (3.1.5), (3.1.7) определяют столько матриц, сколько элементов содержит матрица , а формулы (3.1.6), (3.1.8) – столько матриц, сколько элементов содержит матрица 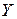. Этот факт, а также наличие двух видов производных для одной и той же функции и вспомогательных матриц  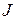и 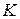 делают изложенный подход мало привлекательным.

Иной подход изложен в работе [124]. Если 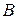 – ( 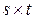)-матрица,  – 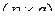-матрица, то производная  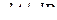определяется как ( )-матрица следующим образом:

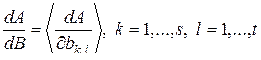.                             (3.1.9)

Например, если  – 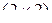-матрица, а  – вектор-столбец с  элементами, то

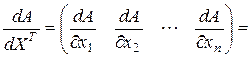
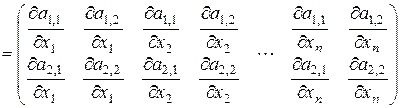.         (3.1.10)

На основе определения (3.1.9) в [124] получены правила дифференцирования произведения, сложной функции и транспонированной матрицы.

Производная произведения двух матриц определяется в [124] выражением

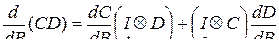,                       (3.1.11)

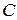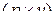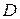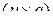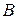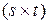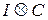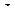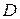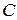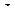где  – -матрица,  – -матрица,  – -матрица, ,  – кронекеровы произведения единичной матрицы  на матрицы  и  соответственно, причем в произведении  матрица  имеет размеры 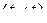, а в произведении  – размеры .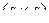

Правило нахождения производной сложной матричной функции записывается в виде

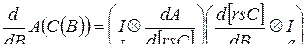.                     (3.1.12)

Здесь  – 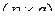-матрица,  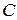– 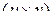-матрица,  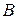– 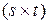-матрица. Единичная матрица  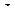в левом декартовом произведении в (3.1.13) имеет размеры 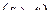, в правом – размеры 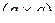. Символы  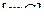означают матрицу-строку размера 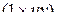, полученную из строк  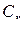матрицы С:

.

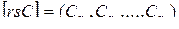Производная транспонированной матрицы определяется равенcтвом

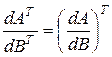.                                           (3.1.13)

Из изложенного видно, что при матричном дифференцировании в [124] используется дополнительное понятие кронекерова произведения, которое является плохо формализованной операцией. При этом основные правила дифференцирования (3.1.11), (3.1.12) оказываются достаточно сложными и неудобными. Кроме того, авторы этой теории не выходят за рамки обычных (двухмерных) матриц.

Дальнейшее развитие теория матричного дифференцирования получила в работе Амосова В.В. и Колпакова А.А. [2]. Здесь для производной скалярной функции 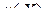 по матрице  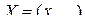принято то же определение (3.1.2), что и в [111]. Получены производные некоторых новых функций по сравнению с [111] (следа, определителя матрицы и др.). Производные (3.1.2) названы в [2] скалярно-матричными.

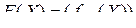
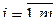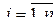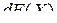Для дифференцирования матричной функции по матричному аргументу (матрично-матричное дифференцирование) в работе [2] введено понятие дифференциала матрицы: если , , – матричная функция от матрицы , то дифференциал  определяется как 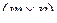-матрица

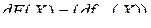,                                    (3.1.14)

где

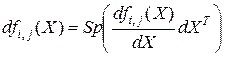,                            (3.1.15)

и 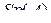 – след матрицы . Необходимо отметить, что нахождение дифференциала не всегда оказывается достаточным. Часто нужно иметь производную. В этом состоит ограничение подхода работы [2]. Кроме того, эта теория относится лишь к обычным (двухмерным) матрицам.

Теория скалярно-матричного дифференцирования позволяет записать три члена ряда Тейлора для скалярной функции 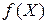 векторной переменной :

,

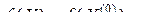
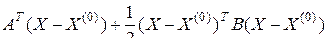где 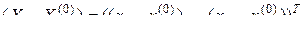– вектор-столбец аргументов функции 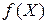, , 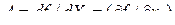, 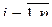– первая производная функции  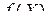в точке 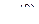, , 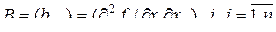– вторая производная функции  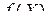в точке 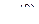. Записать последующие члены ряда Тейлора с помощью векторно-матричного подхода и теории скалярно-матричного дифференцирования не представляется возможным.

Различные определения матрично-матричных производных можно найти в работе [23]. Их особенностью является то, что они не выходят за рамки теории обычных (двухмерных) матриц. Для достижения этой цели в обсуждаемых определениях и правилах дифференцирования используются кронекеровские произведения или векторные упорядочивания. Поскольку указанные операции относятся к плохо формализованным, то рассматриваемые в работе [23] подходы также следует считать плохо формализованными.

К многомерным матрицам относятся работы Милова Л.Т. [39,40]. В [40] дано определение многомерно-матричной производной и рассмотрены некоторые ее свойства. Многомерно-матричная производная определена на основе понятия многомерной матрицы. Многомерная матрица  определяется как совокупность многоиндексных элементов 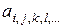. Все индексы предлагается делить на строчные и столбцовые и обозначать многомерную матрицу символами 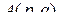, где  и 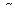 указывают количество столбцовых и строчных индексов соответственно, а размерность матрицы равна . Числа  и 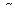 в пределах равенства  можно выбирать произвольными, а для отнесения индекса к строчному или столбцовому предложены правила помечивания индексов. Строчный индекс помечивается символом “-”, столбцовый – символом “+”. Помечивание начинается с последнего индекса, который, если 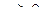, принимается строчным. Следующий индекс принимается столбцовым, если 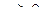. Далее строчные и столбцовые индексы чередуются до тех пор, пока не исчерпаются либо строчные, либо столбцовые индексы. В первом случае все оставшиеся индексы принимаются столбцовыми, а во втором – строчными [39]. Многомерно-матричная производная

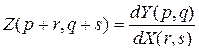
определяется в [40] как 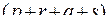-мерная матрица, состоящая из частных производных от элементов  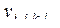матрицы  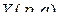по элементам  матрицы 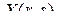, причем принимается, что в матрице  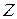столбцовые и строчные индексы матрицы  следуют за столбцовыми и строчными индексами матрицы 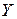 соответственно и соблюдаются правила помечивания индексов. Так, если 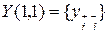, , 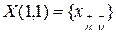то производная  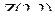имеет элементы

.

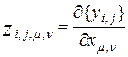На основе приведенного определения в [40] рассмотрены различные случаи многомерно-матричного дифференцирования. Например, получено, что

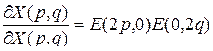,                        (3.1.16)

где

,

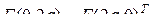
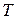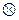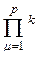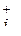 – символ транспонирования, – знак кронекеровского произведения двух сомножителей,  – знак кронекеровского произведения  сомножителей,  – единичный столбец, имеющий все нулевые элементы, за исключением равного единице элемента, стоящего в позиции .

Обсуждаемая теория многомерно-матричного дифференцирования базируется на понятии многомерной матрицы строчно-столбцовой структуры. Это существенно ослабляет связь теории дифференцирования с теорией многомерных матриц Соколова Н.П., в которой такая структура многомерной матрицы не предполагается. При этом изменяется определение транспонированной матрицы, не используются такие важные понятия, как 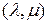-свернутое произведение матриц, 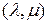-единичная матрица и т.д. Кроме того, результаты теории дифференцирования представляются достаточно громоздкими и плохо формализованными. Это можно видеть хотя бы на примере производной (3.1.16), в которой используется плохо формализованная операция кронекеровского произведения.

В последующих разделах разрабатывается теория многомерно-матричного дифференцирования, полностью базирующаяся на теории многомерных матриц Соколова Н.П.