Определение. Математическим ожиданием 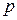 -мерно-матричного случайного процесса
-мерно-матричного случайного процесса 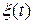 (1) называется
(1) называется 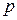 -мерная матрица
-мерная матрица 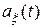 , определяемая выражением
, определяемая выражением
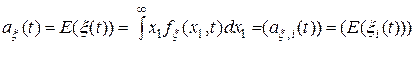 , (5)
, (5)
где 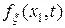 – одномерная плотность вероятностей случайного процесса
– одномерная плотность вероятностей случайного процесса 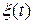 (1),
(1),  – аргумент одномерной плотности вероятностей.
– аргумент одномерной плотности вероятностей.
Для стационарного в узком смысле процесса математическое ожидание не зависит от времени.
Определение. Конечномерным ( 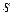 -мерным) математическим ожиданием
-мерным) математическим ожиданием 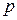 -мерно-матричного случайного процесса
-мерно-матричного случайного процесса 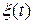 (1) называется
(1) называется 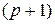 -мерная матрица
-мерная матрица 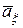 , являющаяся математическим ожиданием матрицы
, являющаяся математическим ожиданием матрицы 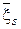 (3):
(3):
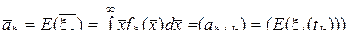 , (6)
, (6)
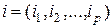 ,
,  ,
, 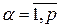 ,
,  ,
,
где 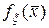 –
– 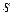 -мерная плотность вероятностей (4) случайного процесса,
-мерная плотность вероятностей (4) случайного процесса,  – аргумент
– аргумент 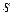 -мерной плотности вероятностей.
-мерной плотности вероятностей.
Определение. Дисперсией 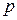 -мерно-матричного случайного процесса
-мерно-матричного случайного процесса 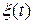 (1) называется
(1) называется  -мерная матрица
-мерная матрица 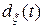 , определяемая выражением
, определяемая выражением
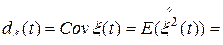
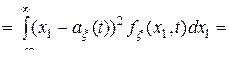
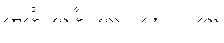 , (7)
, (7)
где 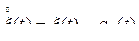 – центрированный случайный процесс,
– центрированный случайный процесс, 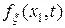 – одномерная плотность вероятностей случайного процесса
– одномерная плотность вероятностей случайного процесса 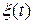 ,
,  – аргумент одномерной плотности вероятностей.
– аргумент одномерной плотности вероятностей.
Дисперсия стационарного в узком смысле процесса не зависит от времени:
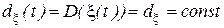 .
.
Определение. Ковариационной функцией 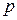 -мерно-матричного случайного процесса
-мерно-матричного случайного процесса 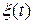 (1) называется
(1) называется 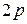 -мерная матрица
-мерная матрица 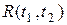 , определяемая выражением
, определяемая выражением
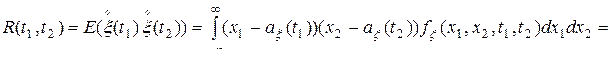
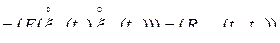 , (9)
, (9)
где 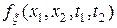 – двухмерная плотность вероятностей случайного процесса
– двухмерная плотность вероятностей случайного процесса 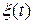 (1),
(1), 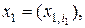
 ,
, 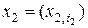 ,
,  , – аргументы плотности вероятностей,
, – аргументы плотности вероятностей, 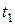 ,
, 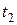 , – два произвольных момента времени.
, – два произвольных момента времени.
Из определения (9) получаем, что дисперсия (7) 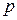 -мерно-матричного случайного процесса
-мерно-матричного случайного процесса 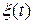 определяется по его ковариационной функции с помощью выражения
определяется по его ковариационной функции с помощью выражения
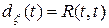 .
.
Для стационарного в узком смысле процесса ковариационная функция является функцией одного аргумента 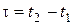 :
:
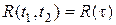 .
.
Отсюда для стационарного процесса
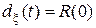 .
.
Поскольку по свойству произведений многомерных матриц выполняется равенство
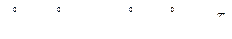 , (11)
, (11)
где
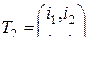
– подстановка на множестве 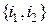 из двух
из двух  -мультииндексов, то получаем следующее свойство ковариационной функции:
-мультииндексов, то получаем следующее свойство ковариационной функции:
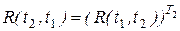 . (12)
. (12)
Для стационарного в узком смысле процесса свойство (12) приобретает вид
 .
.
Определение. Конечномерной ( 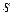 -мерной) ковариационной матрицей
-мерной) ковариационной матрицей 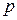 -мерно-матричного случайного процесса
-мерно-матричного случайного процесса 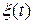 (1) называется
(1) называется 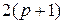 -мерная матрица
-мерная матрица 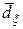 , являющаяся математическим ожиданием матрицы
, являющаяся математическим ожиданием матрицы 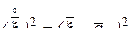 :
:
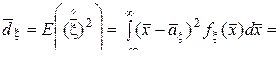
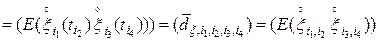 , (8)
, (8)
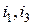 –
– 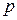 -мультииндексы,
-мультииндексы, 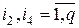 – индексы,
– индексы, 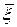 определяется выражением (3),
определяется выражением (3), 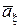 – выражением (6).
– выражением (6).
Определение. 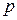 -мерно-матричный случайный процесс
-мерно-матричный случайный процесс 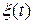 (1) называется гауссовским, если его
(1) называется гауссовским, если его 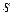 -мерная плотность вероятности определяется выражением
-мерная плотность вероятности определяется выражением
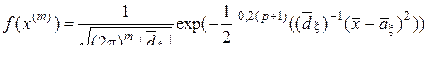 , (10.2.16)
, (10.2.16)
где 
 – определитель матрицы
– определитель матрицы 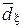 , под которым будем понимать определитель матрицы,
, под которым будем понимать определитель матрицы, 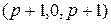 -ассоциированной с матрицей
-ассоциированной с матрицей 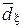 ,
, 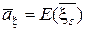 – математическое ожидание матрицы
– математическое ожидание матрицы  ,
,  – аргумент
– аргумент 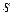 -мерной плотности вероятностей,
-мерной плотности вероятностей, 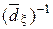 – матрица,
– матрица, 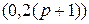 -обратная к матрице
-обратная к матрице 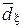 ,
, 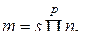 .
.
Гауссовскую плотность вероятности (10.2.16) будем обозначать обычным образом 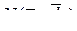 .
.
Дата: 2019-02-02, просмотров: 421.